In the previous posts, we have primarily used colour to differentiate between positive and negative values. In this second last video of the adding and subtracting integers series, we look to explicitly introduce the symbolic notation used to represent negative integers.
The video shown at the top of the post has the entire visual progression of integer addition using symbolic notation.
See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.
Visual Prompts: Question 1, Act 1
Watch the first 52 seconds of the video above before pausing.
The video shows the following integer situation which should be familiar if the previous integer posts have been explored already:
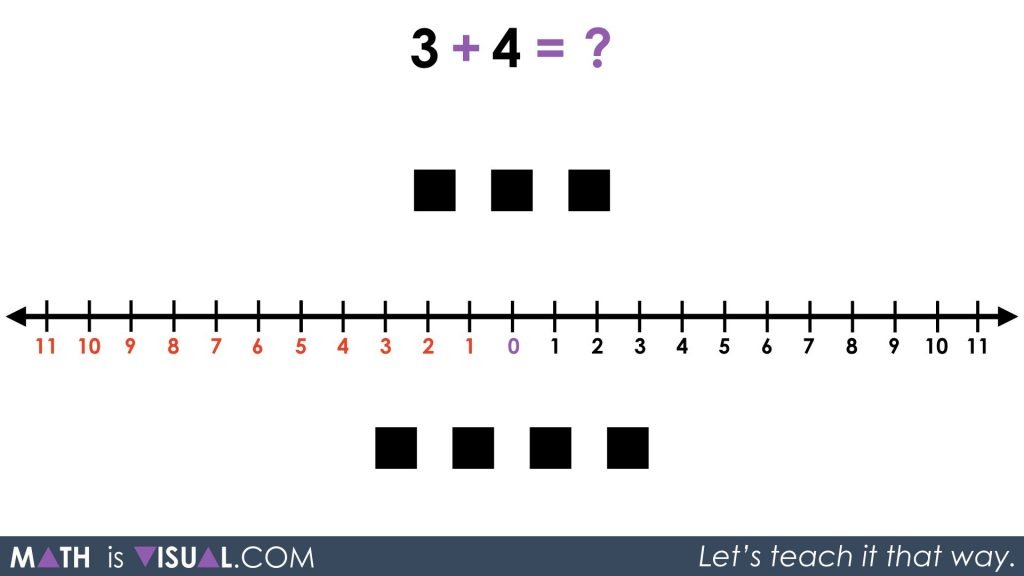
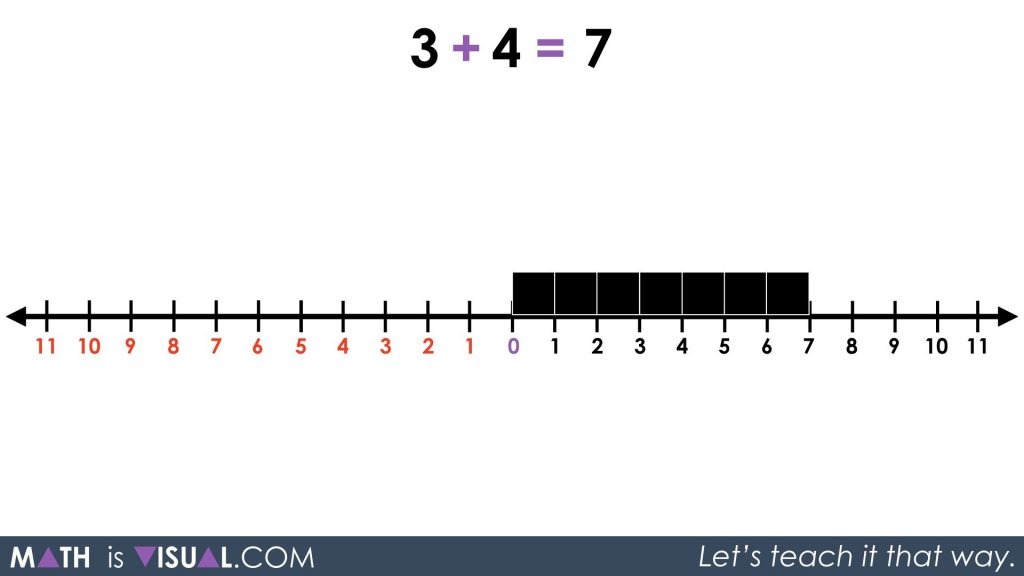
For most students, this first prompt will be a fairly easy warm-up with or without the number line with a result of 7.
Then, students are given a visual of 4 red squares added with 6 black squares.
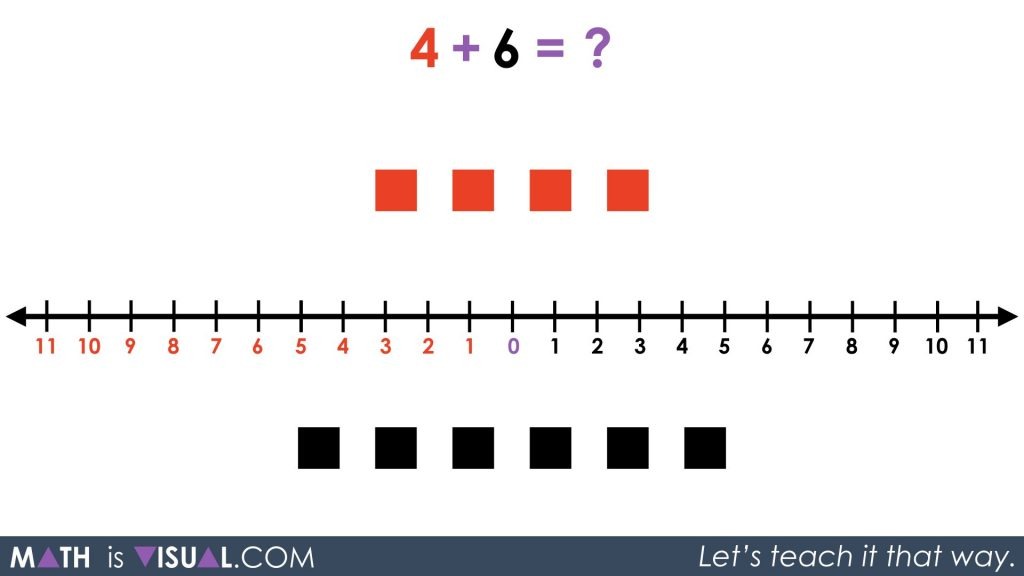
Students will recall from the previous integer posts that combining a red and black square will make them disappear. This is the visual representation of the zero principle, which is very important for students to understand conceptually what is happening when we work with integers.
In the video, the red and black squares are laid out on the number line as we see below.
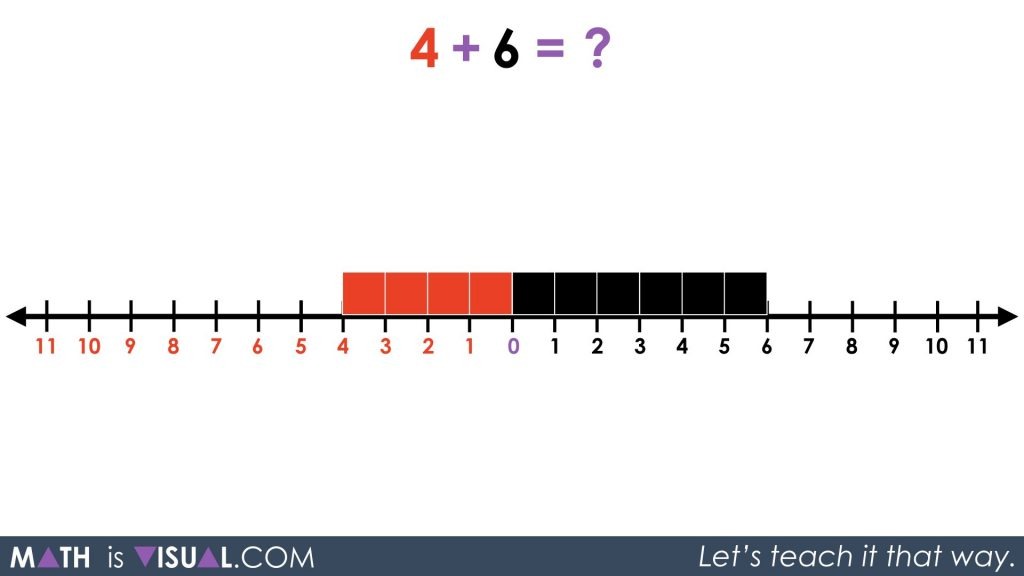
At this point, I would recommend that you pause the video and allow your students or your children attempt coming up with the solution.
After they have been given a chance to work through this problem, you can resume the video.
The Math Is Visual animation will show that 4 red squares combine with 4 black squares and disappear leaving only 2 black squares remaining.
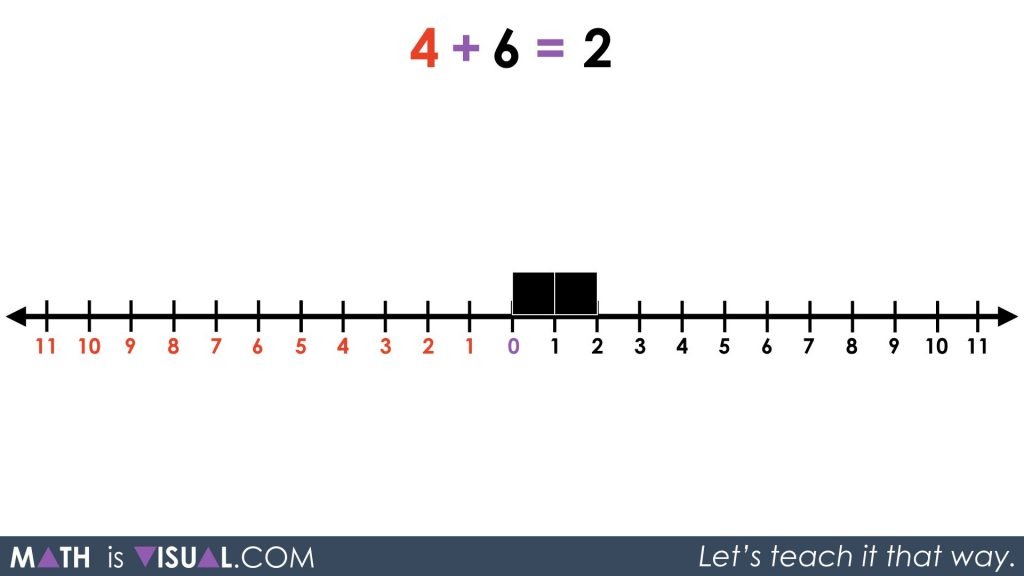
This is where we finally formally introduce the symbolic notation used to represent the red squares. Instead of using the colour red, we are going to replace the colour red with a hyphen or a “negative” sign.
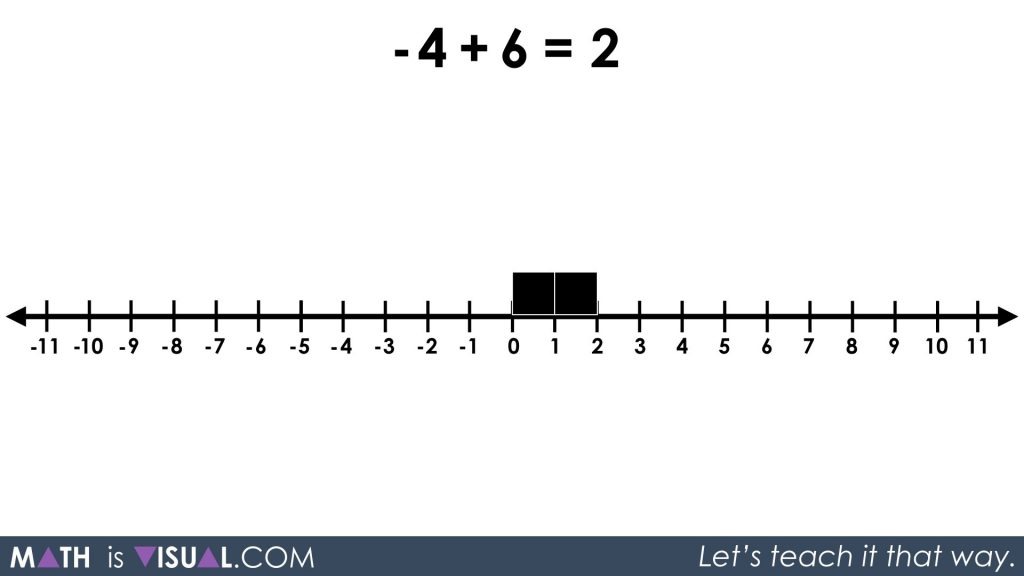
It is important for the teacher or parent to clarify to the participant that the hyphen can be used to represent the operation of subtraction, but also to represent a negative value algebraically. This is very heavy and complex for students to understand initially, so that is why I believe in doing a lot of work visually to ensure they build their fluency with this idea.
Next up in the video, we let students wrestle with some symbolic notation for the first time. Pause the video at the 1 minute, 45 second mark when you see the following:
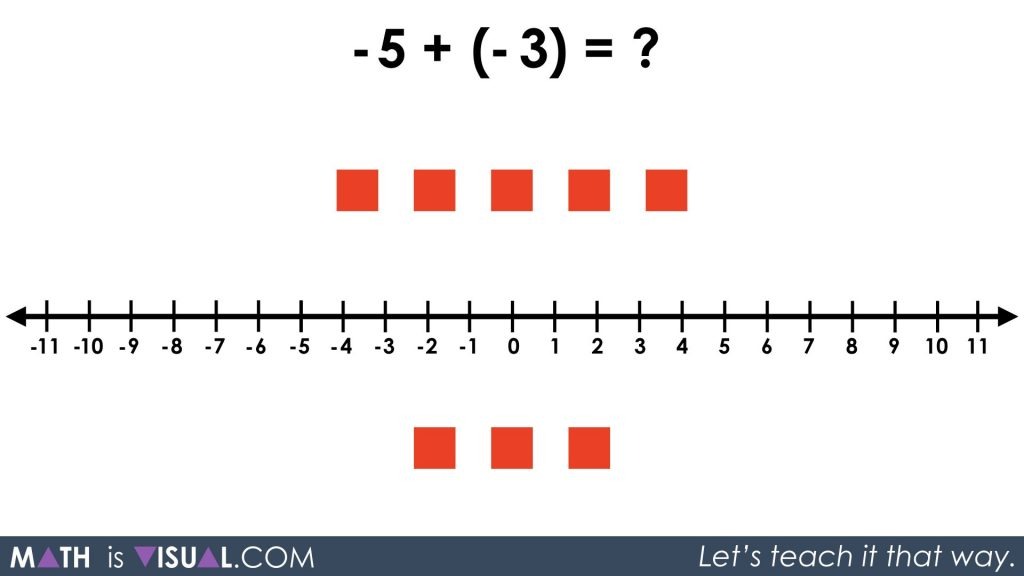
By this point, I would be anticipating that students will be able to see that 5 red plus 3 red results in 8 red. While I’d likely continue speak in terms of colour at least initially, I would want to make the connection that this is the same as saying -5 + (-3) will result in -8 total.
While I would expect some students to struggle with the new symbolic notation we have just introduced, I would hope that they could come up with “8 red” as a result. If they are still struggling to identify how many squares in terms of colour will result, then you probably want to back up the bus and do more work there prior to introducing the symbolic notation.
After giving you students an opportunity to solve this problem, you can resume the video and see the 8 red squares or -8 on the number line.
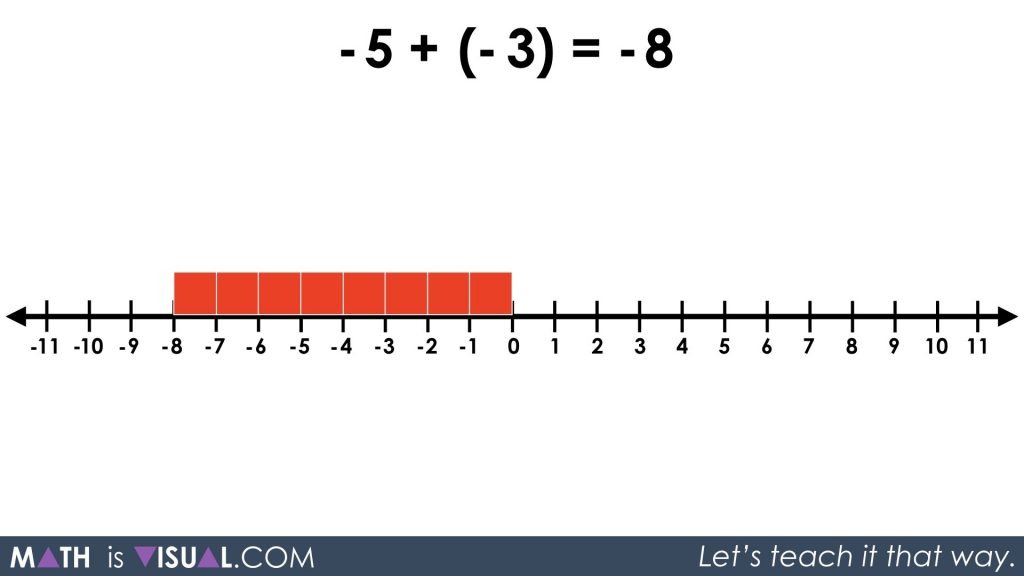
Finally, we will give students one more problem to wrestle with.
Pause the video at the 2 minutes, 22 second mark when you see the following:

Giving your children an opportunity to use physical square tiles or counters would be beneficial here and even drawing out their own number line would be useful.
Have them line up the tiles like we see here:
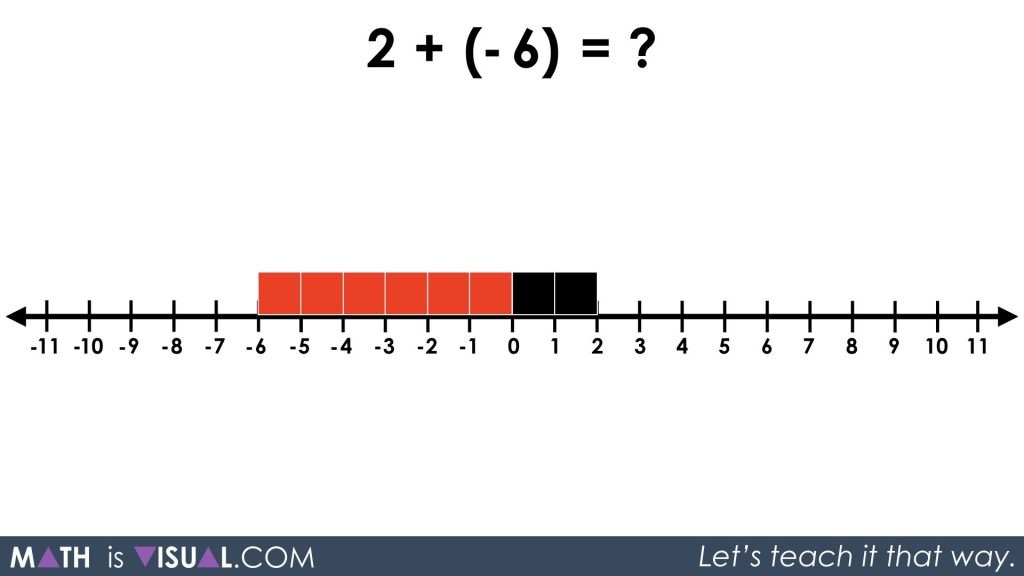
Then, have them use the zero principle to make two black and two red tiles go away.
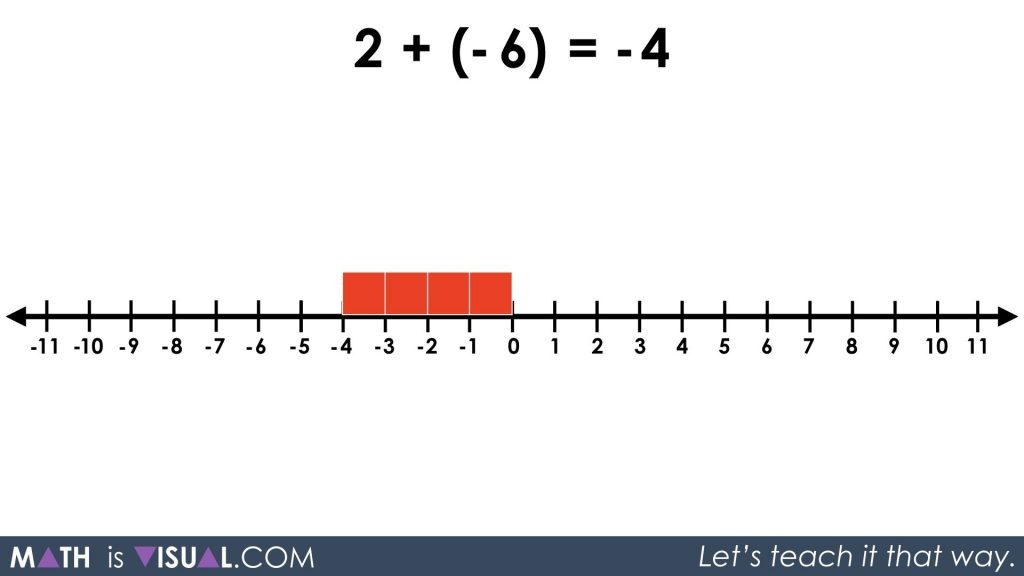
In other words, we had 4 and subtracted 4.
Or, 4 – 4.
Or, 4 + (-4).
Or, -4 + 4.
In any case, we end up with 4 of each “type” cancelling out because of the zero principle.
Watch in the next few days for the final video that will use symbolic notation for integer subtraction.
Let me know in the comments how you used this activity!




Add comment