Theoretical Probability

In this Math Is Visual Prompt, students are given the opportunity to wrestle with the idea of probability through a question in the 2018 Education Quality and Accountability Office (EQAO) Standardized Test for Grade 6 Mathematics release materials. While questions that come up on the EQAO standardized assessment for mathematics tend to look quite dry and “wordy” on the surface, they are great questions that are easy to solve for students who have experience attacking problems concretely and visually using mathematical models and representations as tools for thinking.

Let’s get started…

Spark Curiosity: What Do You Notice? What Do You Wonder?

As I do in most every 3 act math task, I use the Annie Fetter “What do you notice? What do you wonder?” to spark curiosity while watching the first portion of this video.

Here’s an image of what students/children will be looking at when you are instructed to pause the video:

After students share what they notice and wonder, you can then show them the next portion of the video until you’re instructed to pause.

Here, students are now able to go ahead and try solving this problem using any mathematical representation they choose. Remember, if they choose to use an abstract solution using numbers and symbols, be sure to ask them how they know that will work. If they don’t have a conceptual understanding, their method will likely be forgotten and/or cause them to get mixed up as things get more complex down the road.

Fuel Sense Making: Visualizing Theoretical Probability

When you move on, you will start to show one of many conceptual approaches to finding the theoretical probability using a combination of a set, area, and linear model.

The reason this is a combination is because you can clearly see the “set” of individual marbles, however they are lined up overtop of a “rectangle” which has area. We are also labelling two variables (number of marbles and whole bag of marbles) using a linear model called a double-number line.

Wow. Definitely a lot going on here. You might need to approach this in sections at first. However, if you build this WITH students, it can be really powerful.

Now, we can partition (or “chop up”) the 20 marbles and the 1 whole bag of marbles by halving:

This is a great start. However, we need to see fourths. So, let’s “fourth” or “quarter” this up:

Great!

Now we can clearly see spatially how much 0.25 of the whole is, however we need to rearrange our marbles to figure out which colour represents a 0.25 chance.

Initially, some might be thinking maybe yellow or orange. Students might need to physically move them to be sure.

After tinkering, you’ll see that 5 orange represents 0.25 or 25 hundredths or 1 fourth of the whole bag and this represents a probability of 0.25.

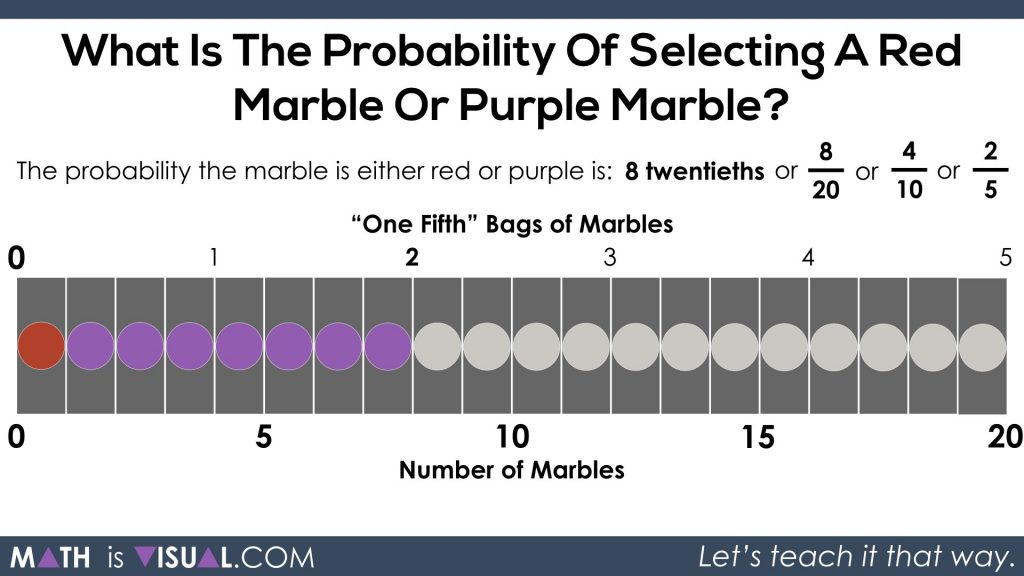
Then, students are asked what the probability of selecting a red or purple marble would be:

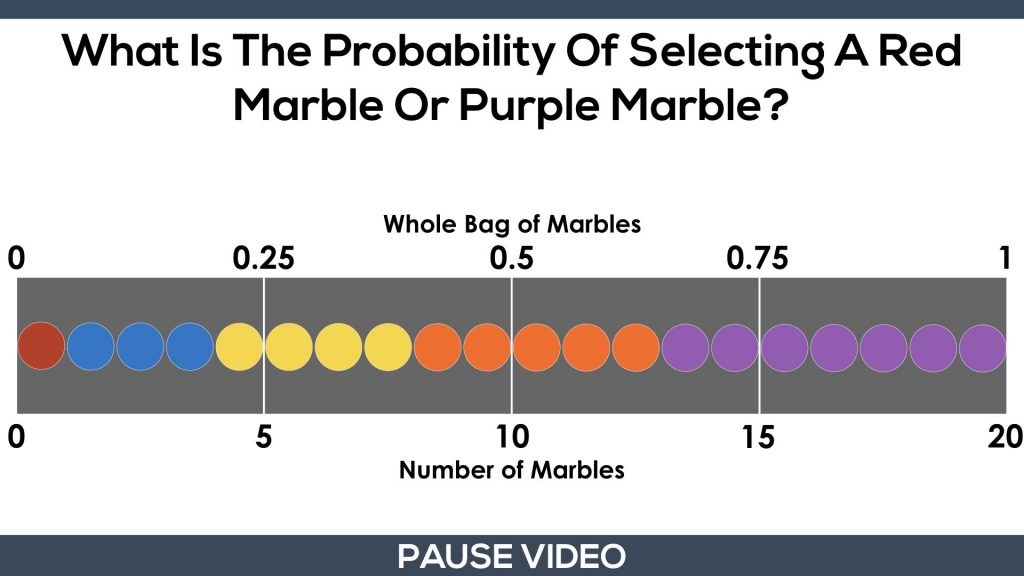
Pause the video and let them give it a shot.

Here’s one way students could tackle this concretely and/or visually.

First, they can partition (chop up) the entire quantity of 20 marbles and the entire bag into 20 parts:

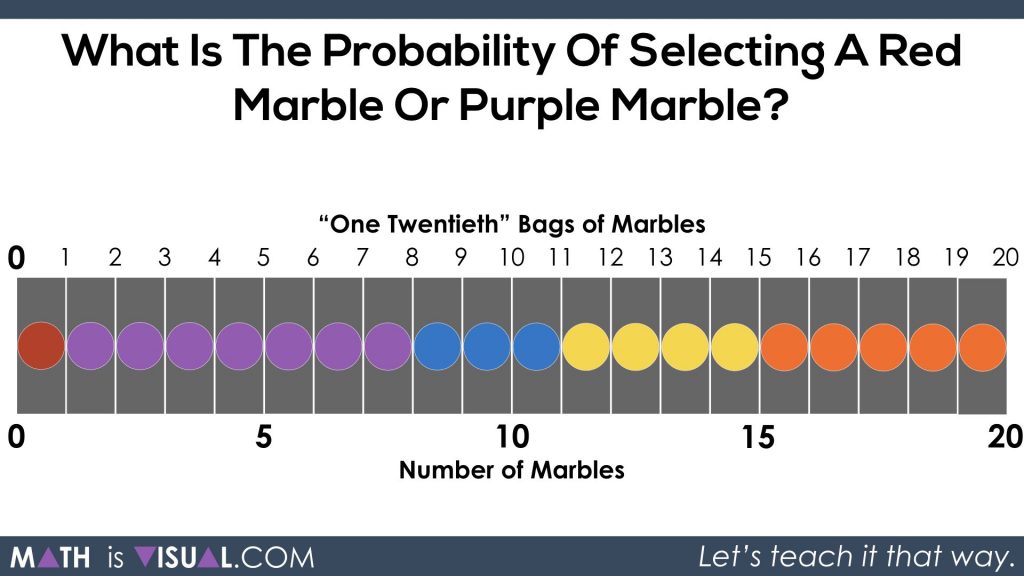
Thus, we can see that the chance of selecting a red or purple marble would be 8 twentieths.

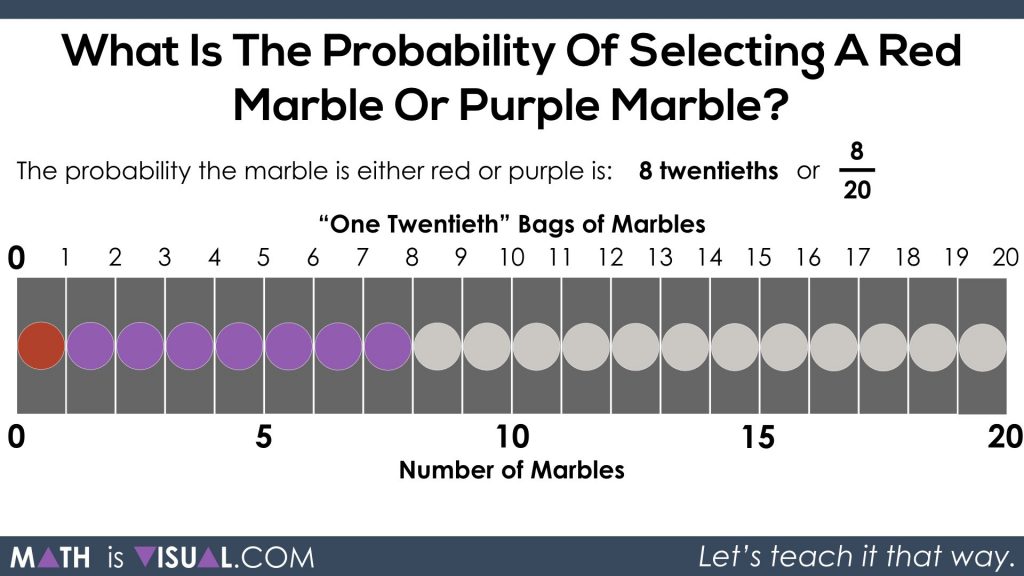
We could also “iterate” or combine parts. For every 2 twentieths we combine, we get 1 tenth:

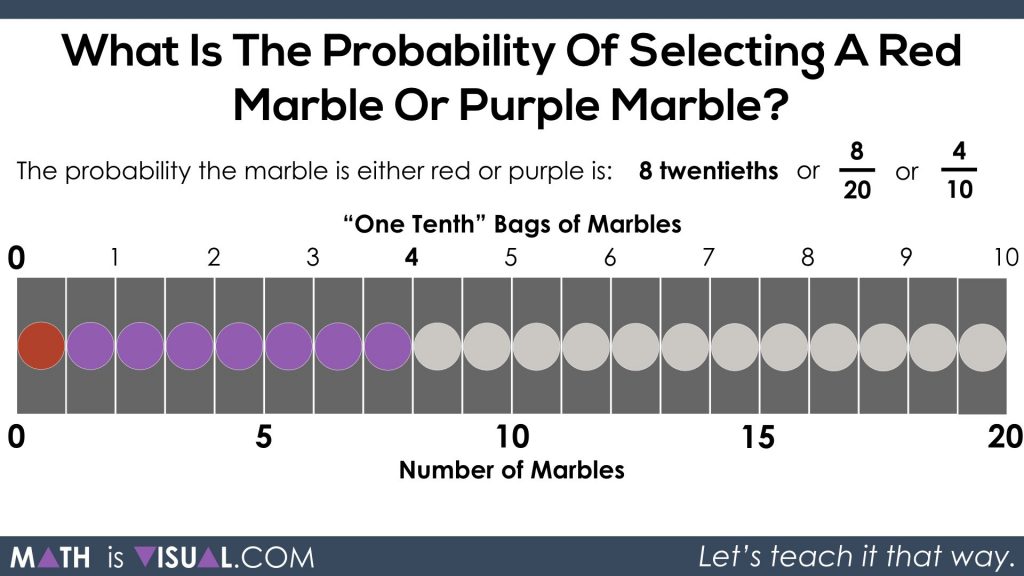
The result shows that the chance is 4 tenths.

For every tenth we combine, we get 1 fifth which results in a chance of 2 fifths:

Pretty awesome what mathematics can do when we approach it from a concrete and visual standpoint first to solidify our conceptual understanding before moving on to steps, procedures, and algorithms!

How’d It Go?

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Ready to dive into a full unit involving probabiliity? Here’s some probability games you can play with your class.

Math IS Visual. Let’s teach it that way.

Dive into conceptual math lessons that engage students and also develop procedural fluency throughout.