In This Set of Visual Number Talk Prompts…
Students will explore scaling composed unit ratios in tandem in order to compare the price of goods. Students will use this information to determine the best value and develop responsible consumerism.
String of Related Problems
In today’s visual math talk, we will be scaling a composed unit ratio in tandem through ratio reasoning. This strategy is useful when trying to compare the price of goods.
Through the context of the price and 12-egg cartons, students will be encouraged to leverage the ratio table to scale this composed unit ratio to reveal other values. Throughout the process, encourage students to share and model their mental math strategies and do your best to model them in the ratio table.
Visual Math Talk Prompt
Show students the following visual math talk prompt & ask:
If the cost for 2 cartons of eggs is $7.20, how much would it be for 4 cartons of eggs?

The first prompt in this string of related visual number talk prompts involves a pretty low floor giving students two quantities that can easily be doubled by decomposing $7.20 into $7 + $0.20.
2($7 + $0.20)
= $14 + $0.40
= $14.40

Next, the visual number talk prompt video asks students to determine the cost for 1, 6, 10 and 12 egg cartons. The goal here is to promote students leveraging their understanding of scaling up and down the ratio table to reveal additional equivalent composed unit ratios.
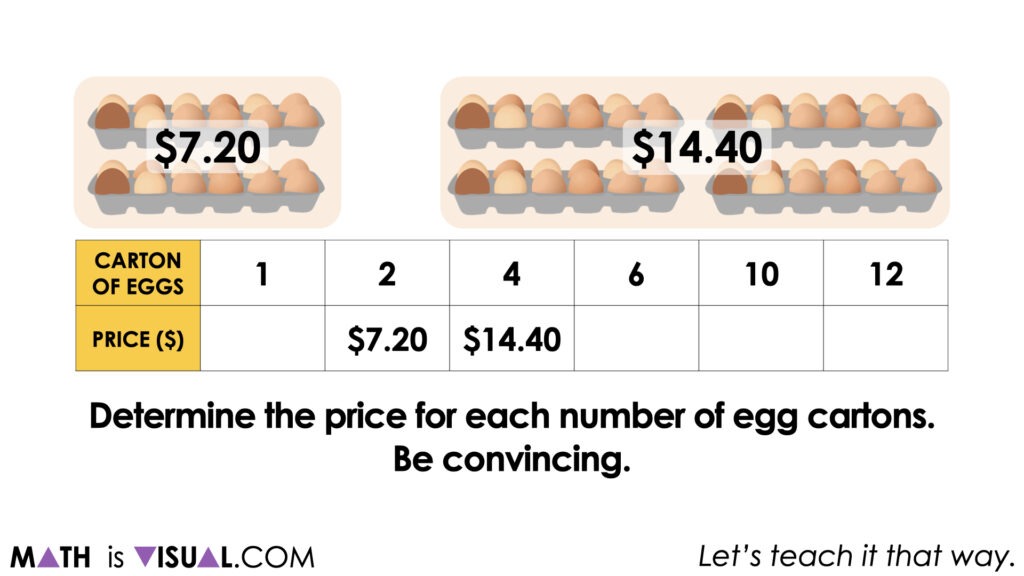
While some may choose to add an additional $7,20 to $14.40 to arrive at $21.60 for 6 egg cartons, others may recognize that they can triple the cost of 2 egg cartons since 6 egg cartons is triple that of 2 egg cartons.
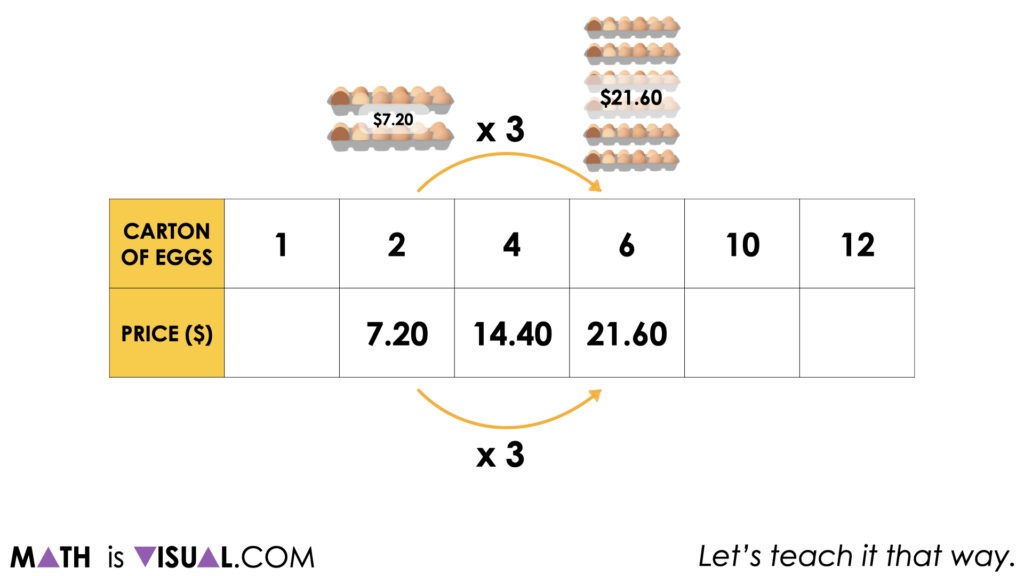
Some students may add $14.40 to $21.60 to reveal the cost for 10 egg cartons since those are the costs of 4 egg cartons and 6 egg cartons (additive thinking).
Others may multiply the cost of 2 egg cartons by 5 since 5 groups of 2 egg cartons is equivalent to 10 egg cartons.
Others still may determine the cost of a single egg carton by halving $7.20 and then scale this by a factor of 10.
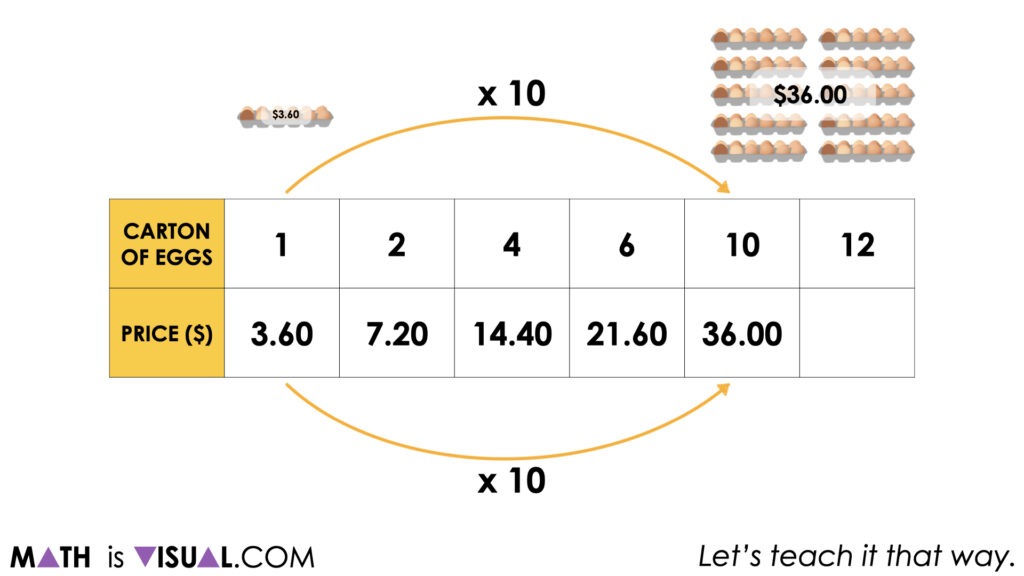
While we will celebrate all approaches used by students via additive and multiplicative thinking, we do want to explicitly highlight the use of scaling in tandem as this is a multiplicative strategy that is very helpful when working with composed unit ratios.
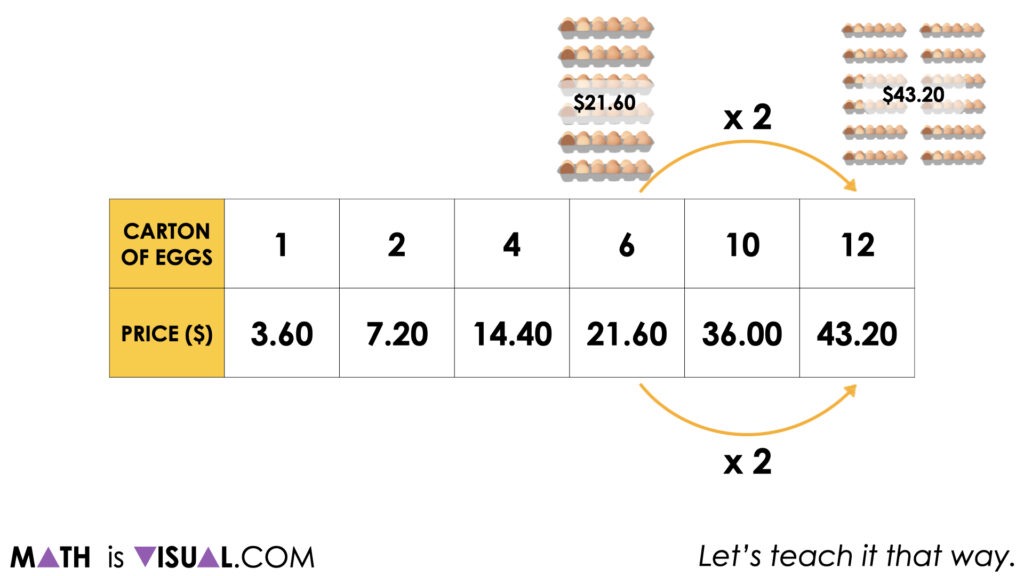
It is worth noting here that while we can see the cost of a single carton of eggs, the rate (or “unit rate” as some call it) is not explicitly shown here.
Only through partitive division of any of these equivalent ratios (i.e.: 3.60:1, 7.20:2, 14.40:4, etc.) can we reveal the rate of $3.60 per carton of eggs.
Interested in learning more about ratios, rates and proportional relationships? Dig into our course, The Concept Holding Your Students Back. The first module has open access for any and all to participate in, so go check it out.
Want to Explore These Concepts & Skills Further?
One (1) additional number talk prompt are available in Day 2 of the Better Buy problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page?
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.



Add comment