Scaling Ratios on the Double Number Line

In This Set of Visual Number Talk Prompts…

Students will explore scaling composed unit ratios in tandem in order to compare the price of goods. Students will use this information to determine the best value and develop responsible consumerism.  

Intentionality…

The purpose of the Day 4 activities is to reinforce key concepts from Day 3 Students will engage in a math talk and will have an opportunity to complete independent purposeful practice. The math talk and purposeful practice serve to develop a deeper understanding of the following big ideas. 

• There are two types of ratios; composed unit and multiplicative comparison;
• A composed unit is often (not always) a ratio with two distinct units; 
• A composed unit can be scaled in tandem; 
• When you divide a composed unit through partitive division, you reveal a rate; 
• Composed units can be scaled to the same quantity of one variable in order to identify the “better buy”;
• Rates can be used to make direct comparisons in order to identify the “better buy”.

Overview of This Visual Math Talk

In today’s math talk, we will use partitive division to reveal a rate. 

For each of the following composed units, ask students to determine a rate. 

2 litres of cola for $3.20

4 litres of apple juice for $5.20

3 pounds of nectarines for $4.80

5 pounds of tomatoes for $7.00

12 pack of batteries for $8.00

Visual Math Talk Prompt #1

Show students the following visual math talk prompt & ask:

The cost for 2 liters of cola is $3.20. Determine a rate for this composed unit ratio. Be convincing and do not use a calculator.

While students are free to leverage any strategy and model as a tool for thinking or to represent their thinking, some may be gravitating towards the double number line and/or the ratio table as a quick means to leverage their scaling in tandem skills.

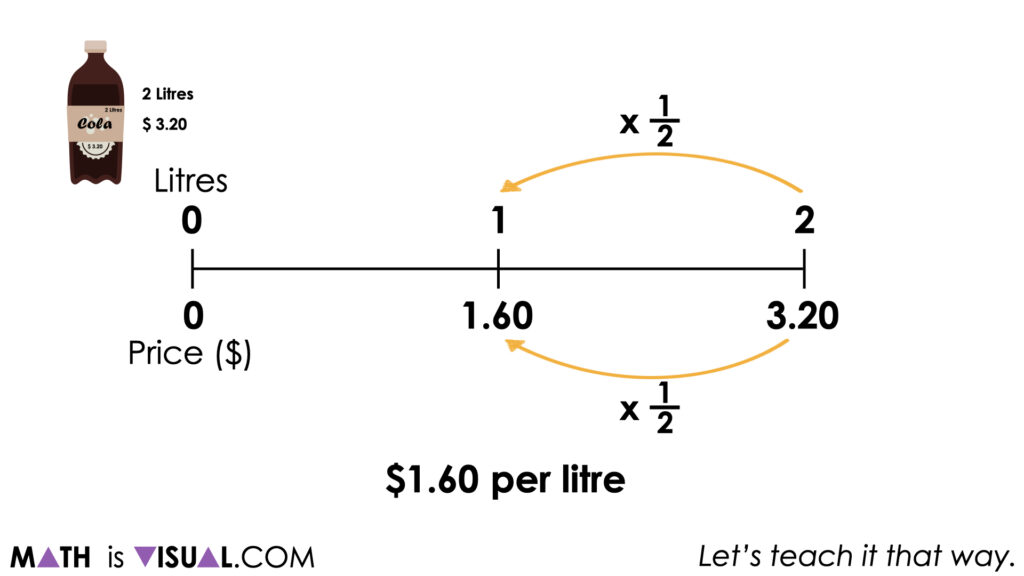
It is worth noting that while we can “see” a rate of $1.60 per litre, the method used was scaling in tandem to reveal a ratio (not a rate) of 1.60:1.

Only when we divide $1.60 by 1 litre through partitive division do we reveal a rate of $1.60 per litre.

Visual Math Talk Prompt #2

Show students the following visual math talk prompt & ask:

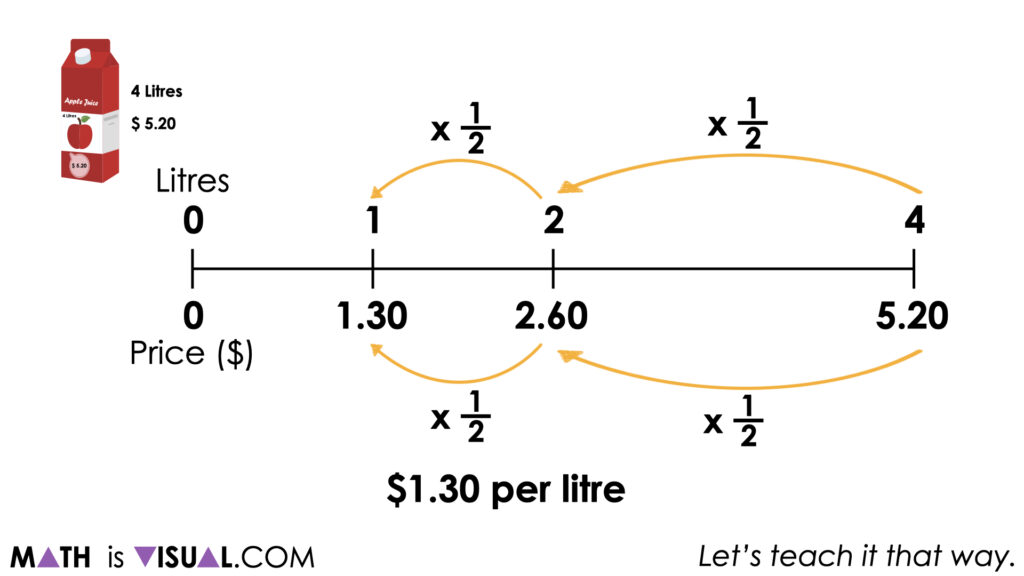
The cost for 4 litres of apple juice is $5.20. Determine a rate for this composed unit ratio. Be convincing and do not use a calculator.

If one has a calculator, the most efficient approach here would be to divide $5.20 by 4 litres through partitive division to reveal a rate in dollars per litre.

Some students may actually use partial quotients to fair share (partitive division) $4 across 4 litres, then fair sharing the remaining “part” of $1.20 across the 4 litres.

$5.20 ÷ 4 litres

= ($4.00 ÷ 4 litres) + ($1.20 ÷ 4 litres)

= ($1.00 per litre) + ($0.30 per litre)

= $1.30 per litre

For other students, they may choose to once again scale in tandem to reveal an equivalent composed unit ratio of $1.30 to 1 litre and intuitively “know” that $1.30 ÷ 1 litre is $1.30 per litre.

Want to Explore These Concepts & Skills Further?

Three (3) additional number talk prompts are available in Day 4 of the Better Buy problem based math unit that you can dive into now. 

Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page?

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.