In This Set of Visual Number Talk Prompts…
Students will continue adding, subtraction and multiplying fractions and decimals by whole numbers. Students will also explore the need for a standard order of operating.
Intentionality…
The purpose of this Visual Math Talk borrowed from the Piggy Bank problem based unit is to reinforce key concepts from the first three days of the unit. Students will engage in a string of related problems through a math talk without the use of a calculator to develop a deeper understanding of the following big ideas:
- Fractions can be represented in a variety of ways;
- Fractions (and their decimal representation) represents values relative to a whole (for example, one whole dollar);
- Quantities represented as a decimal are fractions limited to base ten denominators (i.e.: tenths, hundredths, thousandths, etc.);
- Standard representation of coin values are expressed as decimal hundredths;
- When the order of operations is not considered, the solution can vary;
- The order of operations can be revealed through the context; and,
- Removal subtraction of a positive value or adding the negative of that same value has the same result, i.e., 6 – 2 = 6 + (-2).
Preparing to Facilitate This Number Talk
The following visual math talk is a string of related problems that are crafted in a way to foster discussion and the construction of viable arguments. As such, they are open ended and have more than one possible response.
As the facilitator of the following visual math talk prompts, be prepared to notice and name the thinking students are using (i.e.: additive thinking or multiplicative thinking).
While you could simply share the first image with the prompt for students, introducing via the silent solution animations provided may be more helpful. Although each visual math talk prompt video models a possible strategy, we encourage you to represent student thinking by drawing on the board or on the screen rather than simply playing the video and ignoring the thinking of your students.
Visual Number Talk Prompt
Students will first be prompted to think about:
What is the total amount of money?
How could you convince your neighbour?

After students are given time to think and strategize with their neighbours, take time to facilitate a discussion and model student thinking using the mathematical model that matches their approach best.
While the models you have used to represent student thinking from the room might be enough for the entire group to be convinced of what the total sum of money will be, you might consider also sharing this silent solution animation or a portion thereof if it helps push thinking forward.
One model that can be helpful here is a tape diagram showing both positive and negative quantities based on the expression given in the original visual number talk prompt.
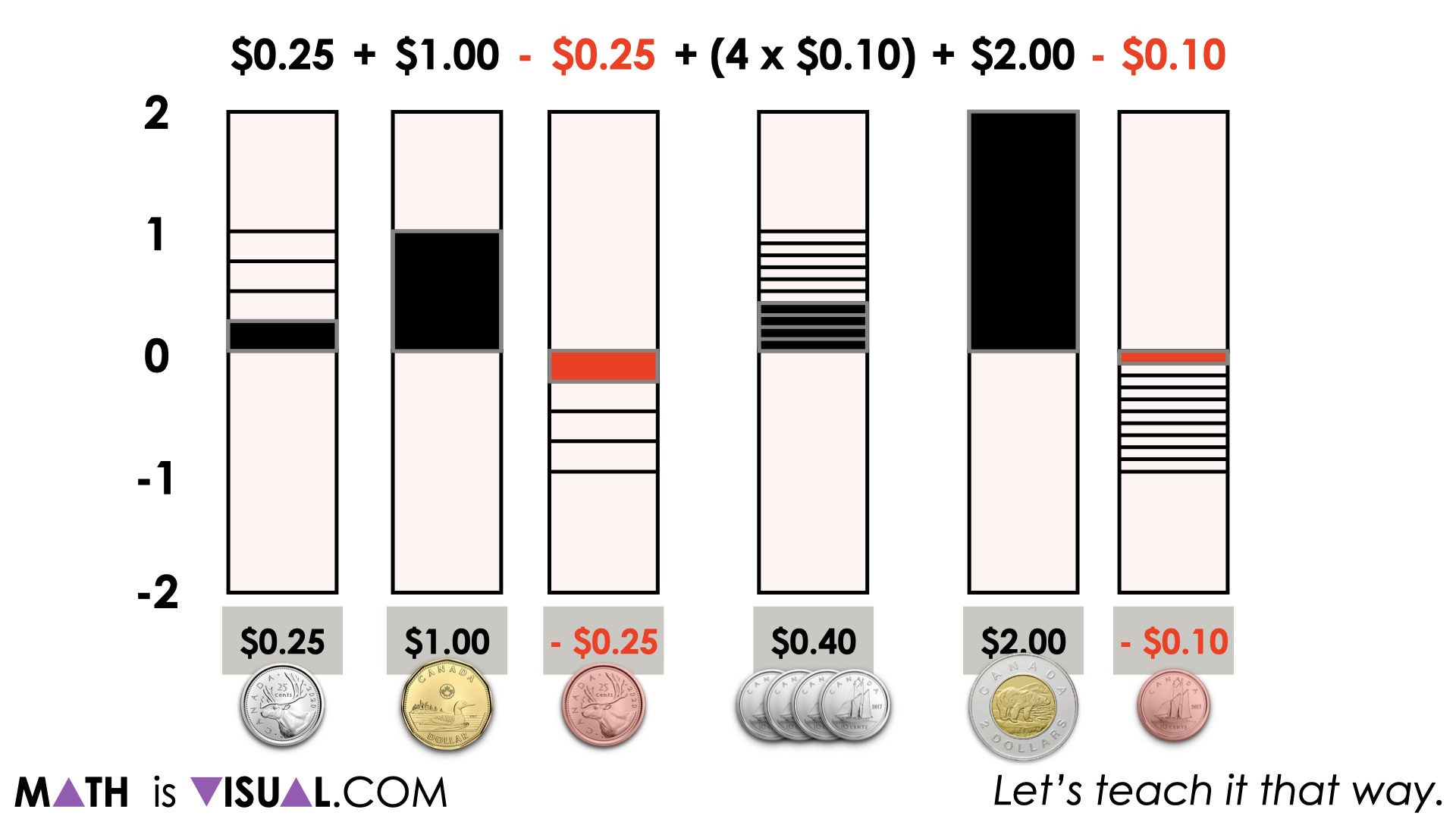
Be sure to highlight the partitions that were used to represent the different quantities (fourths/quarters of a dollar for quarters, tenths for dimes, etc.).
It might also be helpful to highlight the use of brackets surrounding the 4 groups of $0.10 in the expression as a means to explicitly “group” those quantities together despite not necessarily requiring the use of brackets.
In the animation, you can also see the use of the zero principle as we cancel positive sums of money with negative sums of money.
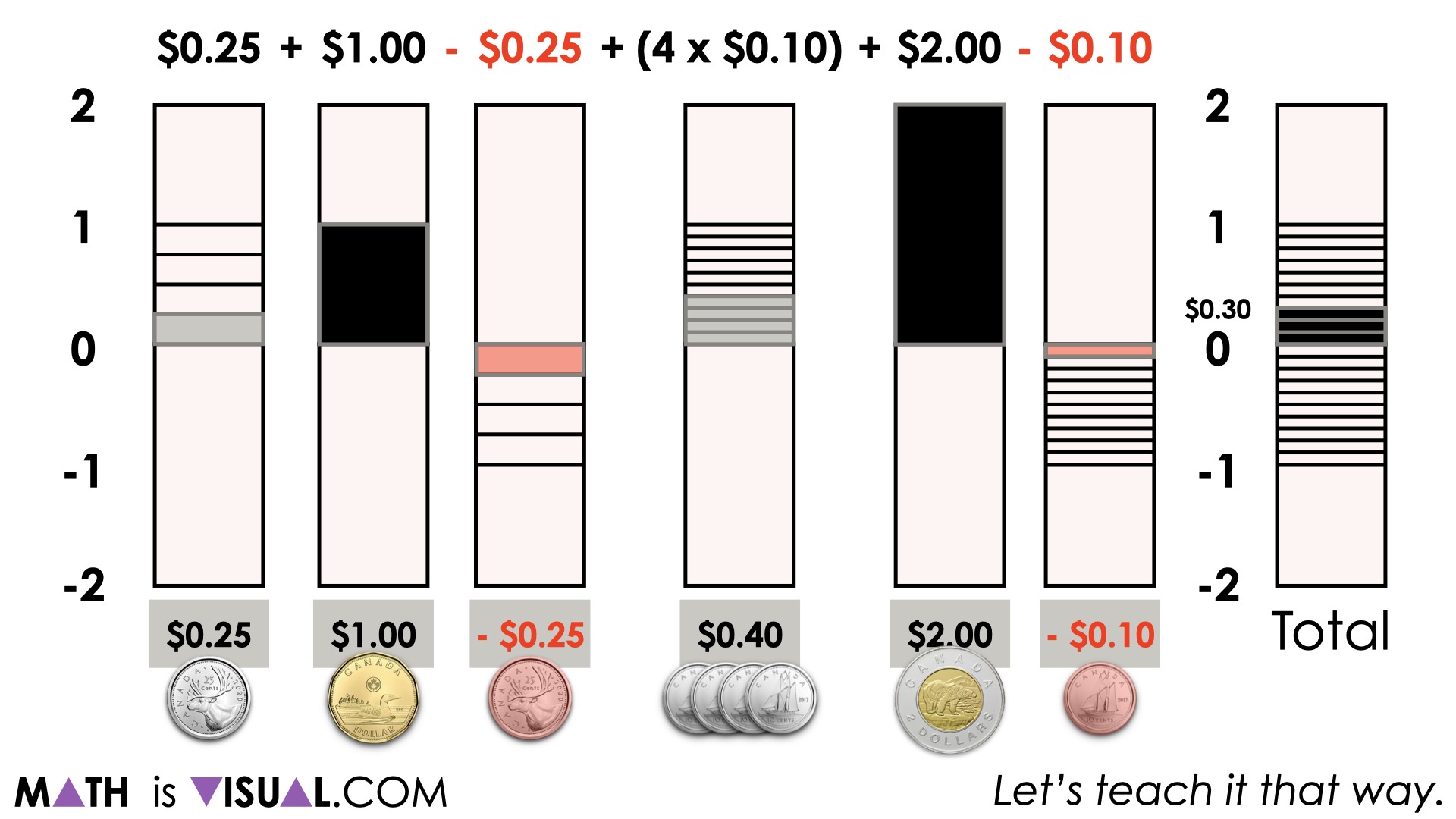
When some students choose to add different quantities (or coins) first, it can be helpful to highlight the use of the commutative property of addition and subtraction being helpful here.
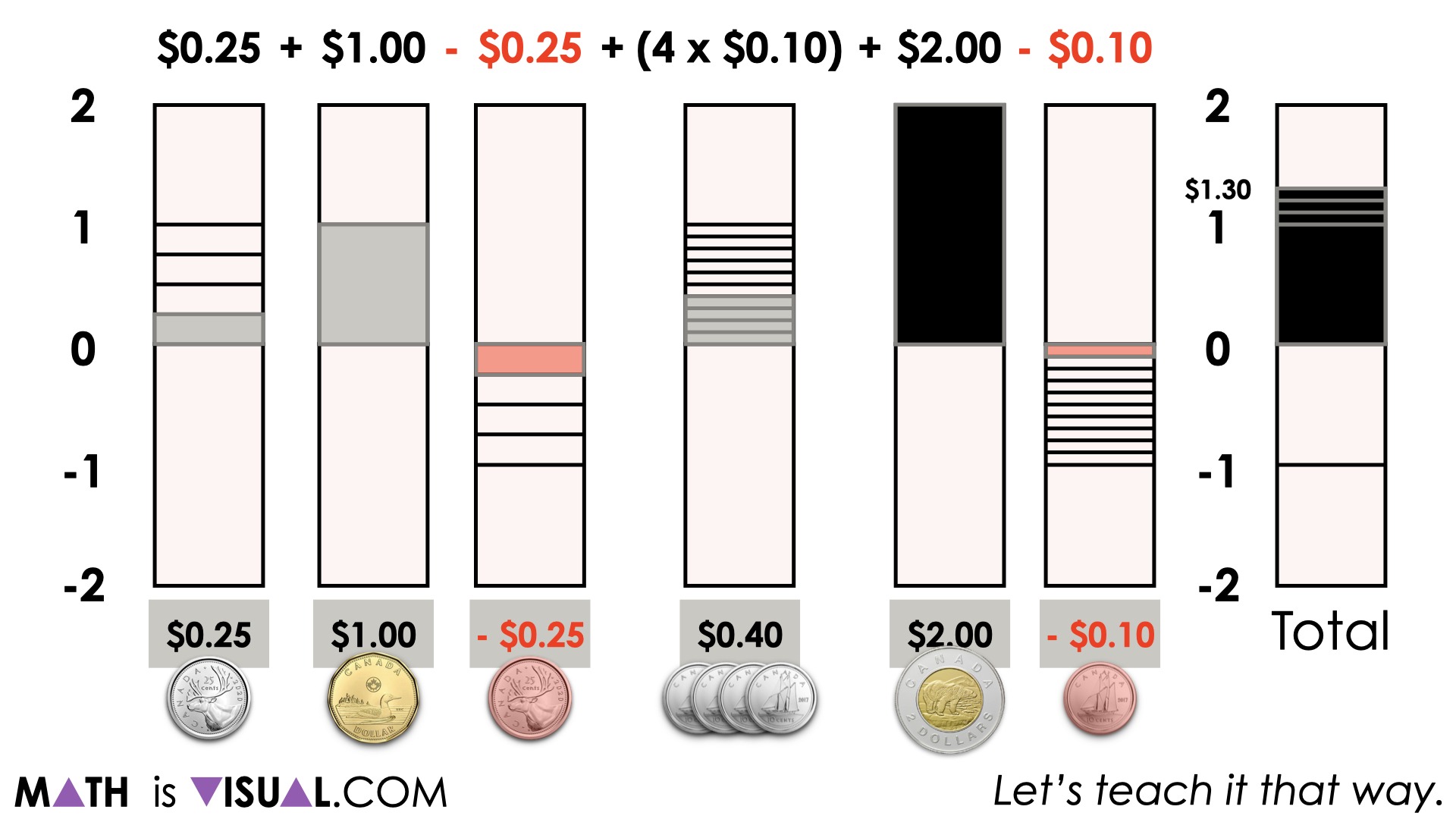
After cancelling out quantities by leveraging the zero principle, we can then begin adding other quantities to determine our sum.
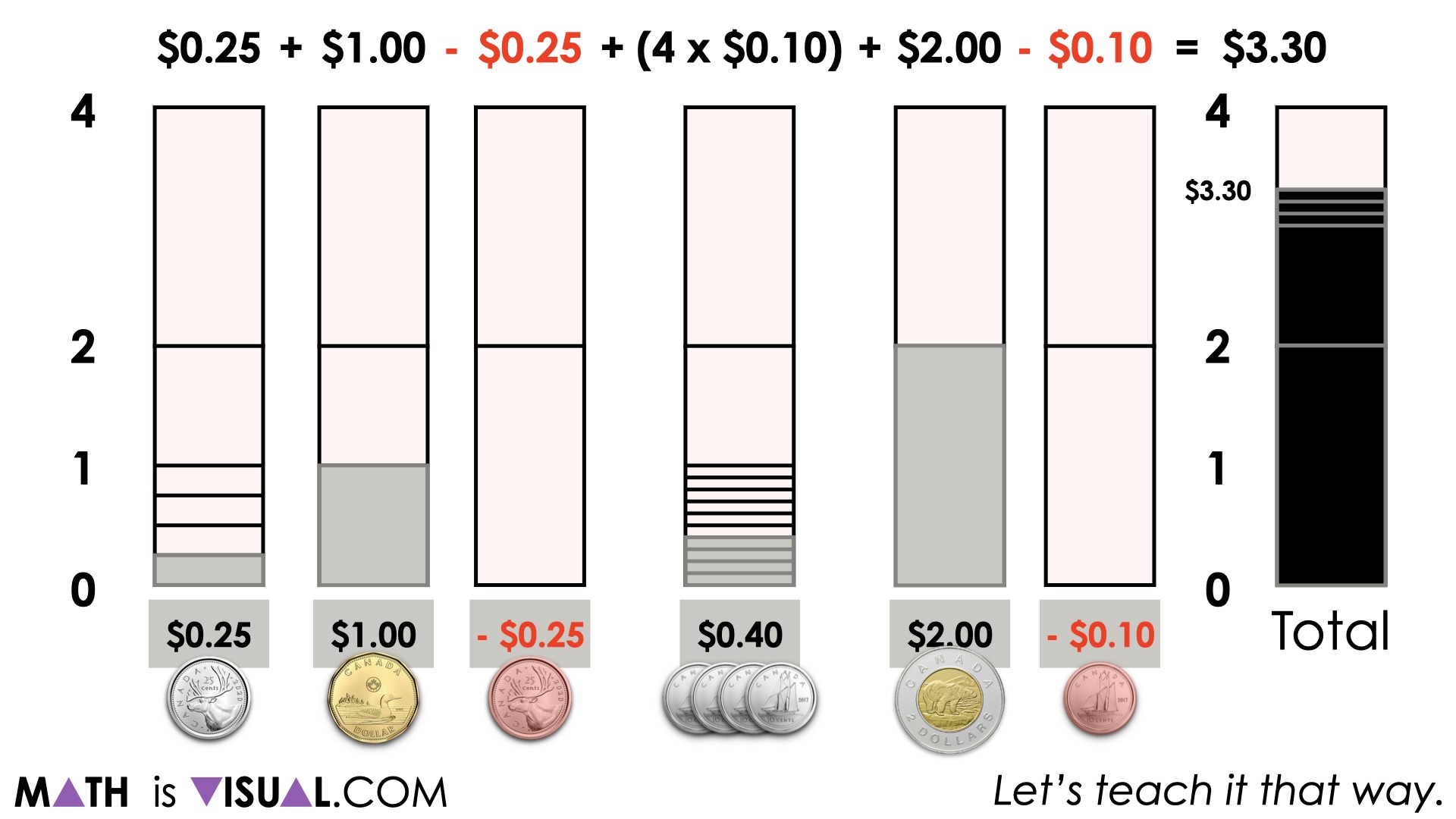
Want to Explore These Concepts & Skills Further?
Dig into the first few days of the Piggy Bank problem based math unit so that you can build the money model with your students.
We also have a huge selection of contextual 3-act math style lessons from the Make Math Moments Problem Based Units page that are worth checking out.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.




Add comment