Conceptualizing The Difference of Squares

I can remember first learning as a high school student and then teaching as a high school teacher the difference of squares property right in the middle of a quadratics factoring unit of study. The only problem is… I never understood why it worked.

In this series of Math Is Visual prompts, we will use the notice and wonder routine from the Curiosity Path to introduce a series of square arrays. With each square array, we’ll remove a smaller square array from within it. 

The question we’ll ask is: what are the dimensions of the rectangular array with the most rows and columns we can create with the remaining tiles?

From this, you’ll be able to see a pattern forming that we know as the difference of squares.

Remember that you can use any set of Math Is Visual prompts as lesson starters, math talks, number talks, or number routines in the classroom or at home with your kids!

As always, do not pre-teach how to solve problems similar to this one. Allow students to investigate by pausing where indicated and to defend their strategies using mathematical models of their choosing.

The silent solution visuals provided after the prompts may be used as a consolidation only AFTER students are given the opportunity to work with these ideas concretely and visually and after consolidating in the classroom through the use of student generated solutions.

Let’s get started…

Sparking Curiosity

Let’s take some time to Spark Curiosity using the Make Math Moments “Curiosity Path” as we always do.

In this case, we will start with showing a series of square arrays and then remove a cube before rearranging:

We provide two more squares, removing 1 square, then rearranging before prompting students to notice and wonder.

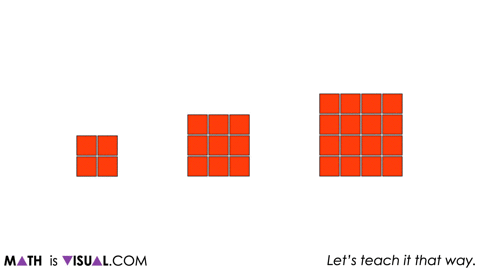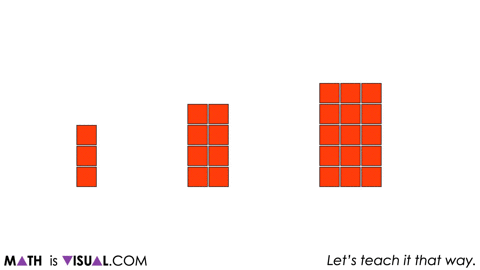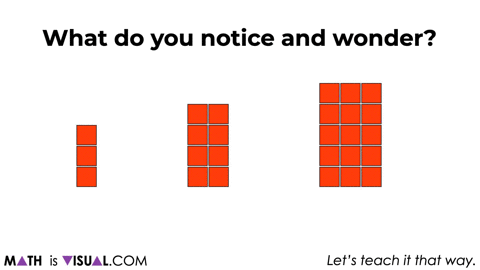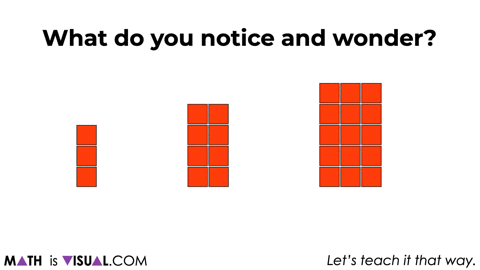
We then share a few more larger square arrays and remove a 2×2 square array from each before rearranging to continue building anticipation.

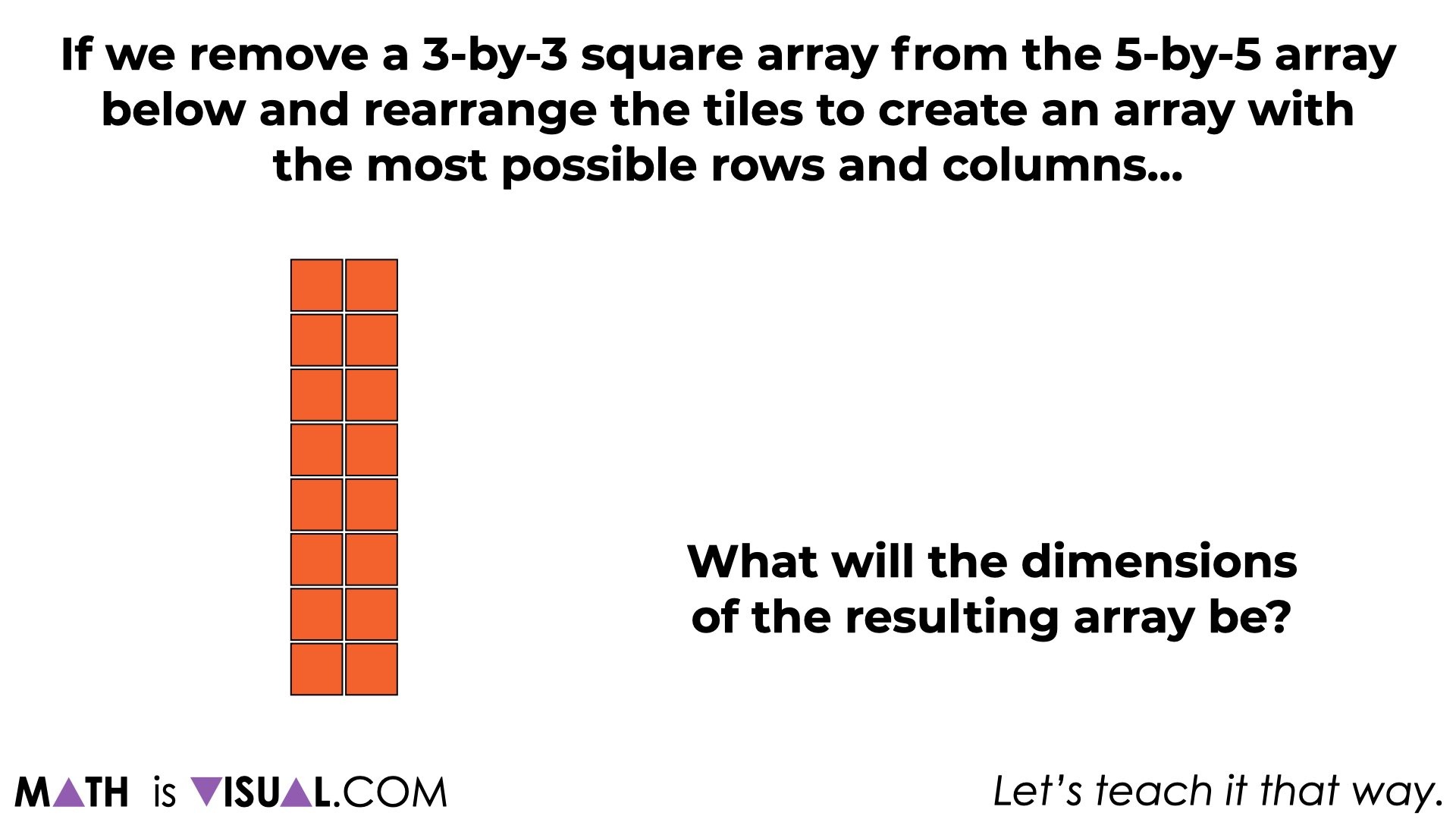
At this point, we introduce a 5-by-5 square array and ask students the following:

If we remove a 2×2 square array from the 5×5 array below and rearrange the tiles to create an array with the most possible rows and columns, what will the dimensions of the resulting array be?

Pause the video here so students have some time to use square tiles, draw, or use whatever other strategies and approaches they’d like.

Then, reveal the resulting array:

At this point, we’ll then ask students a similar question for a 7×7 array removing a 4×4 array using an area model forcing more abstraction.

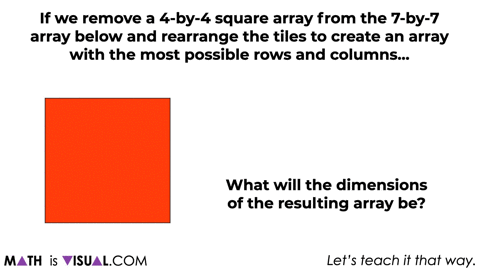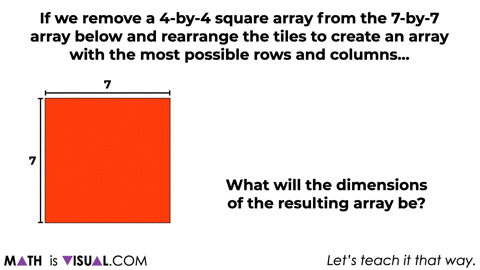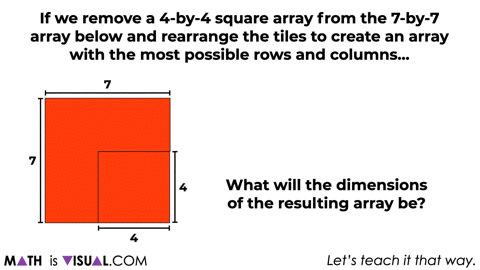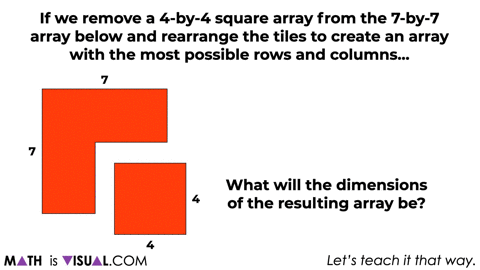
Give students some time to work through this before moving on.

Use student generated solution strategies to help make connections to the pattern that is forming here.

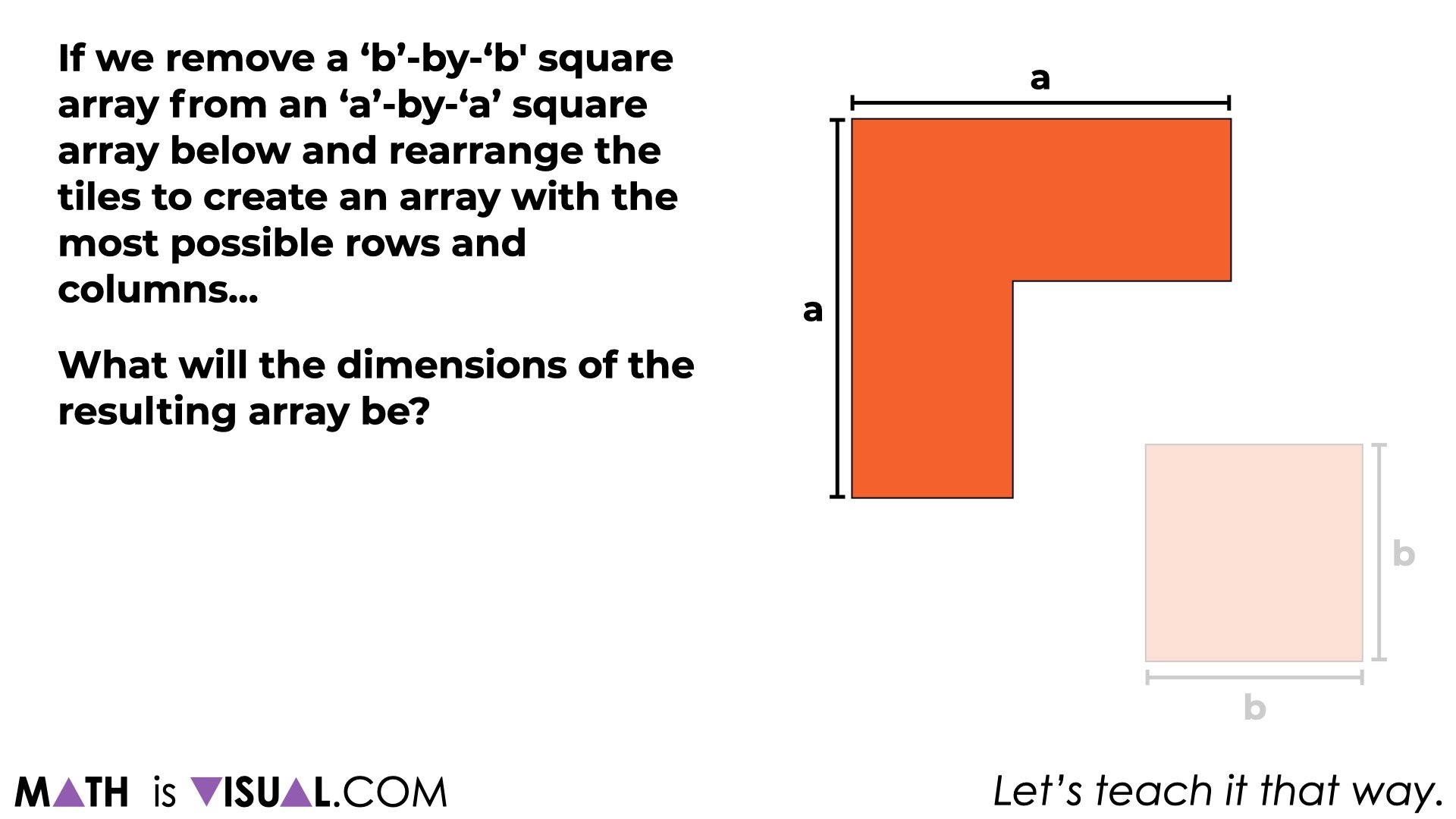
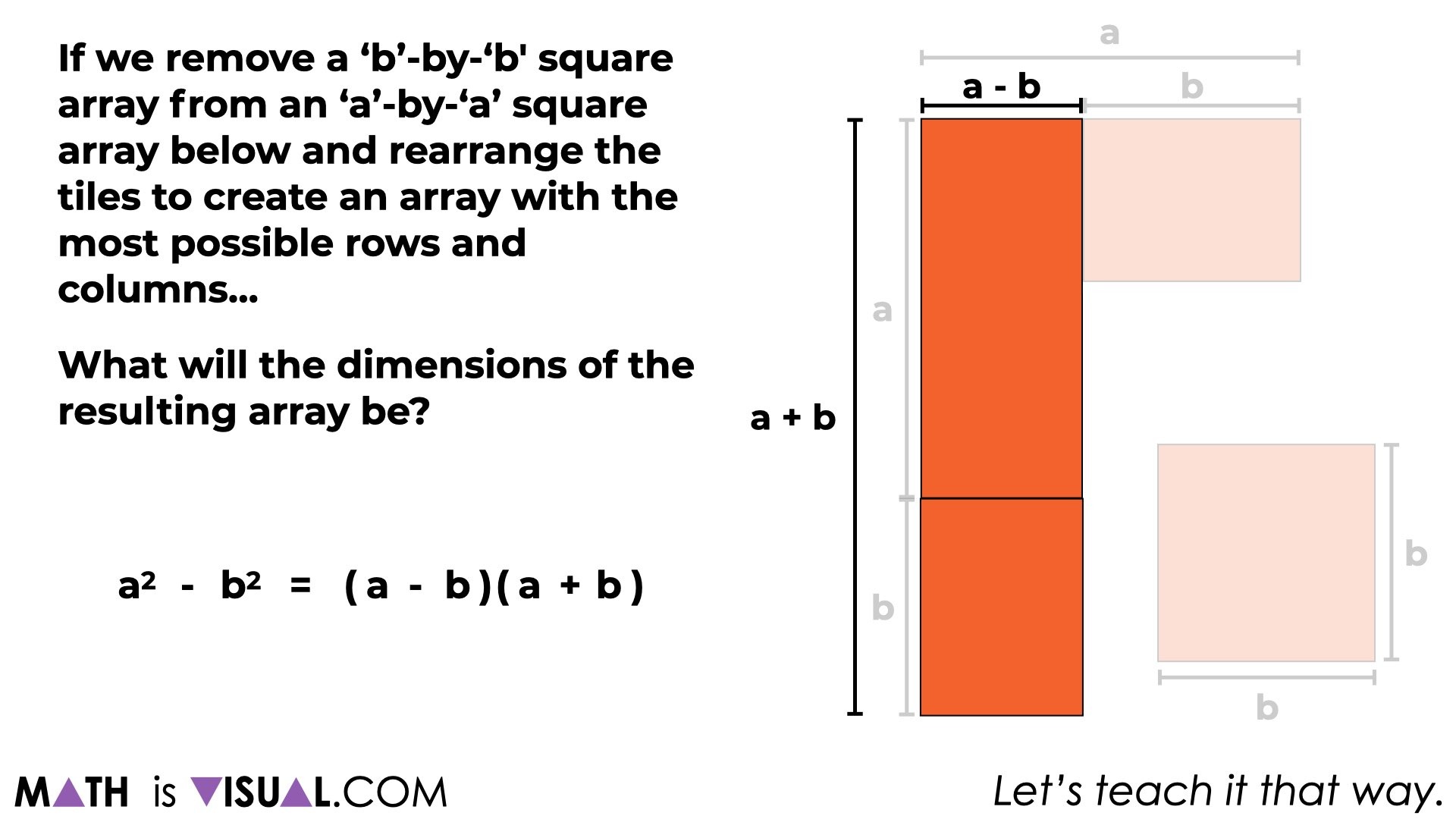
Finally, we’ll leave students with the opportunity (if developmentally appropriate for the students you’re working with) to make connections to the algebraic generalization for the difference of squares:

How many cubes would be left after removing 6 groups of 5 cubes?

Hopefully students will see the relationship of subtracting the length of b from a for one of the dimensions of the new rearranged array and how we’ll need to add the length of b to a for the other dimension.

Hopefully you agree that this particular set of visual prompts is a much more constructivist approach to allowing students to bump into the idea of difference of squares conceptually rather than simply sharing a rule that must be memorized like I did for so many years in the classroom.

Let’s start concrete and work our way to visual mathematical models prior to pushing word problems and symbolic notation before they are ready. 

====

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.