Revealing Scale Factors Through Quotative Division

In This Set of Math Visual Prompts…

Students will explore multiplicative comparison ratios and reveal scale factors through quotative division.

Intentionality…

This set of visual math talk prompts is taken from the Math Talk section of Day 4 in the Make Math Moments Problem Based Unit called Planting Flowers. The purpose of the Math Talk is to reinforce key concepts and big ideas from the first day of this problem based math unit including: 

• There are two types of ratios; composed unit and multiplicative comparison;
• A composed unit is often (not always) a ratio with two distinct units; 
• A composed unit can be scaled in tandem; 
• Equivalent ratios are derived from the same rate; 
• When you divide a composed unit through partitive division, you reveal a rate. 

This set of visual math talk prompts, we will explicitly emerge the idea of revealing a scale factor from a ratio through quotative division.

Preparing to Facilitate

Present the following multiplicative comparison ratios one at a time. Create a context to define the units for each ratio. Focus on ratios with the same units. For each ratio, determine the scale factor. How many times greater. Encourage students to use a model to justify their thinking. 

For the first problem in this string, your prompt might sound like:

One rosebush is currently 32 cm tall, while a tulip is 8 cm tall. How many times taller is the rosebush than the tulip? What fraction of the whole rosebush is the height of the tulip?

If you begin with a context comparing lengths, then you might consider continuing with length comparisons. 

32 : 8

42 : 6

55 : 10

30 : 9

As an additional opportunity to extend, you can also explore the smaller quantity relative to the larger if you feel it is appropriate based on student readiness. For example, 32 is four times greater than 8 or you could say that 8 is one fourth as great as 32. 

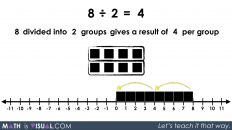
32 cm ÷ 8 cm per group = 4 groups

8 cm ÷ 32 cm per group = ¼ groups

You can learn more about rates, ratios and the roadmap to proportional relationships through the course: The Concept Holding Your Students Back. and/or by diving into the full 5-day problem based unit where this visual math talk is embedded.

Problem #1 

The first visual math talk prompt in this string of related problems is related to the multiplicative comparison ratio 32:8 comparing the height of a rosebush and a tulip.

We begin with comparing how many times bigger the 32 cm rosebush is than the 8 cm tulip.

While students are encouraged to leverage the strategy and mathematical model of their choosing, modelling for the group using bars or a double number line can be helpful to see the iterations of one quantity compared to the other to reveal a scale factor.

Problem #2

Then, we also ask students what fraction of the whole rosebush is the height of the tulip.

Some of the same models can be leveraged to now multiplicatively compare the height from the other perspective. Now, we’re looking for how many fractional iterations or copies of the rosebush height can we see in the height of the tulip?

It will soon become apparent that the tulip is 1 fourth the height of the rosebush and therefore, we can say that the tulip is 1 fourth times as tall as the rosebush on average.

Want to Explore These Concepts & Skills Further?

This visual math talk is just a small snippet of the full string of related problems that are included on Day 2 of the Planting Flowers problem based unit over on the Make Math Moments website.

The full 5-day unit of ratios and rates real world lessons can be accessed on the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.