Here’s another post to add to the integer operation series inspired by David Petro, who had given me some interesting ideas to ponder after I released the last integer multiplication post.
He shared the following ideas to inspire the visuals I put together for this post:
- Visually show the commutative property
- Add a visual showing the fact that 3 x (-5) is the same as -(3×5)
- Use the above rules to show that -3 x 5 = 3 x (-5) = – (3×5) using the above rules
- Now we can try -3 x (-5) which is a mystery. But we know that it can be rewritten as -(3x(-5)) from #3 and we can show that this is visibly the same as 3×5.
After letting that stir in my mind for a week or so, I took some time to sit down and play with these ideas. I think (hope) I came up with something close to what he was visualizing.
Check out this second crack at the entire visual progression of integer multiplication.
See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.
Visual Prompt #1
In the video above, pause at the first question which we can prompt the viewer to to guess the expression being presented by the following visual:

The dots were presented 5 at a time in rows which strategically creates a 3 by 5 array. Thus, the expression could be one of the following:
3 groups of 5
or
3 x 5
Pretty easy stuff so far.
Visual Prompt #2
In the second visual prompt, pause the video at this frame where we can spend some time thinking about the expression:

Again, a pretty basic 3 by 5 array, except now the squares are red and thus represent negative values:
3 groups of -5
or
3 x (-5)
We can pretty intuitively see that multiplying a positive by a negative will yield a negative result.
A prompt for your child and/or students might be:
Will all cases of a positive times a negative yield a negative result?
Visual Prompt #3
The third question begins with the sentence:
Take Away 3 groups of 5
Be sure to pause the video here and have your child/student think about what this actually means. If we think back to the integer addition and subtraction videos earlier in this series, we may recall that if you want to subtract values that are not there, we can use the zero principle to “create” squares. Recall that since 1 black square and 1 red square result in zero, we can create as many “zero pairs” as we’d like.
In this case, it would make sense to create 3 groups of 5 positives and 3 groups of 5 negatives.
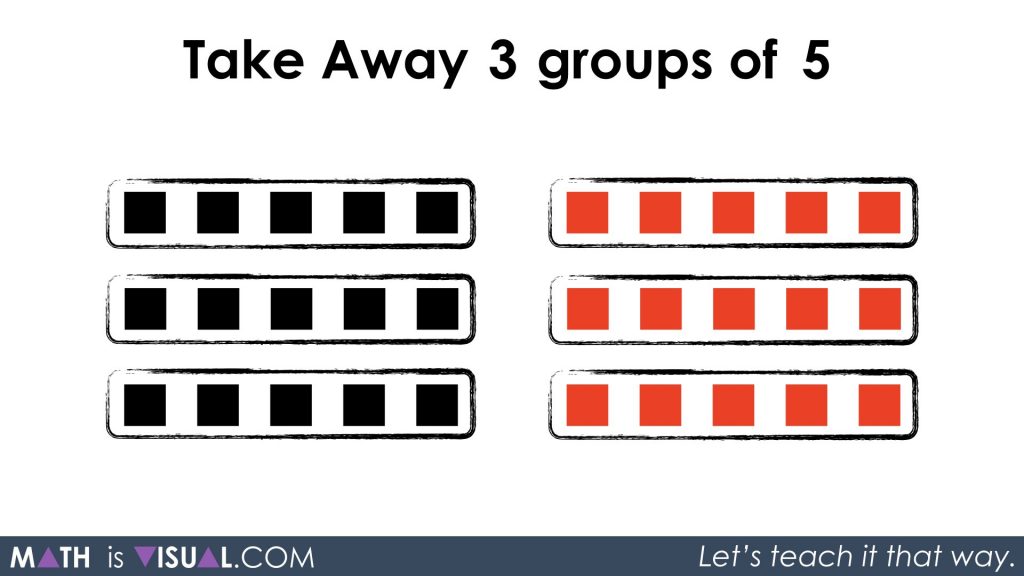
By taking away 3 groups of 5, we are left with 3 groups of -5 or -15 total:
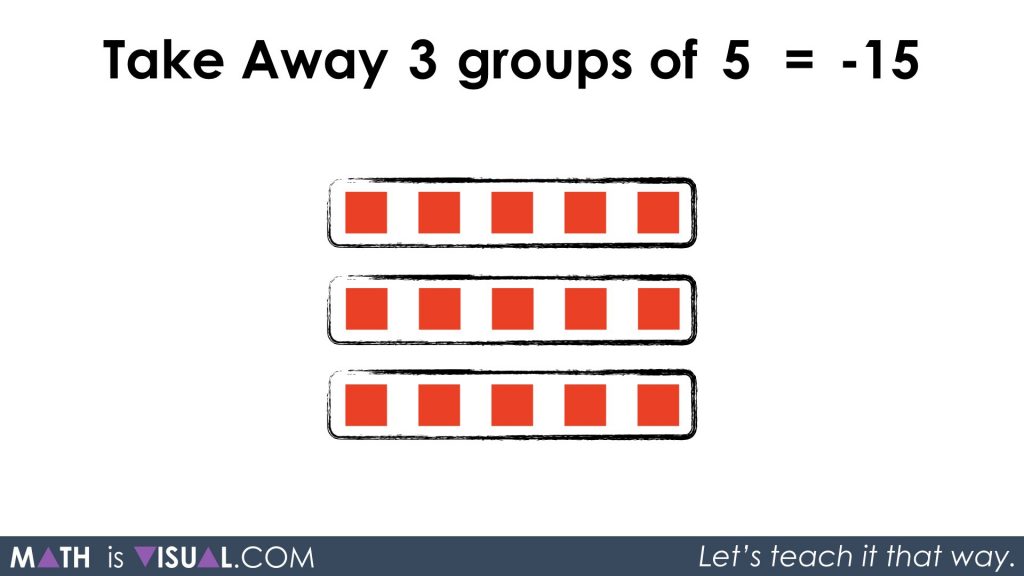
We can also write this as subtracting 3 groups of 5 from 0 like this:
-(3 x 5) = -15
Or, as we see in the video, we can also think of it as subtracting 3 groups of 5 positives which sounds the same verbally, but mathematically we can write this:
-3 x 5 = -15
May need to do a few more examples like this with students and concrete manipulatives to ensure they understand this before moving on.
Visual Prompt #4
Multiplying a negative by a negative is the most fun because this is the least intuitive of all the integer multiplication rules. However, if we think about multiplying negatives with words first, we get this:
Take away 3 groups of -5
Be sure to pause the video and again have your students think about what we must do if there are no squares to take away.
YES! The zero principle!
We need to “create” 3 groups of 5 and 3 groups of -5 which we know is the same as zero:
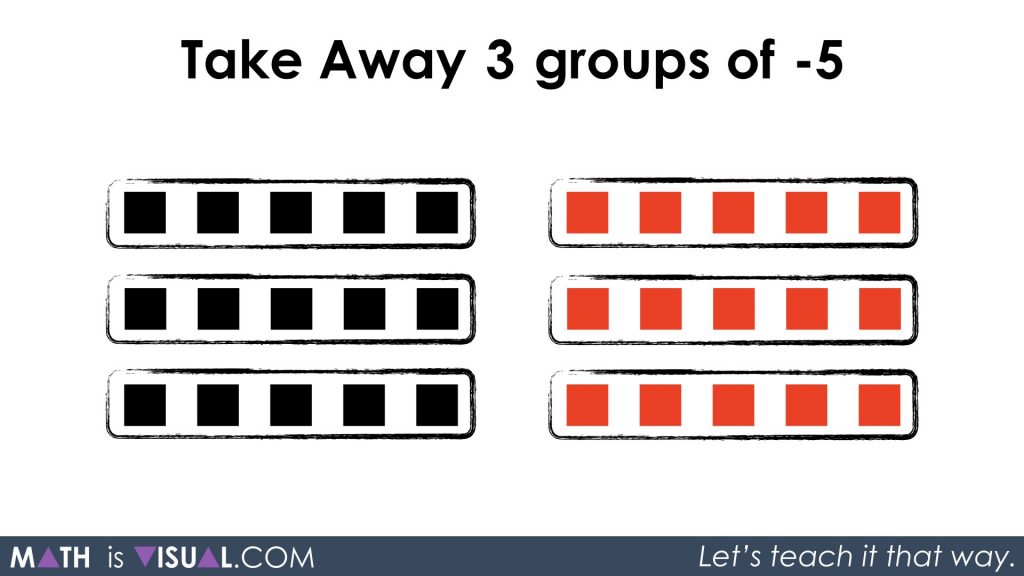
By doing this, we can now take away our 3 groups of -5 and we will quickly see we are left with the 3 groups of 5 black squares or 15 positives:
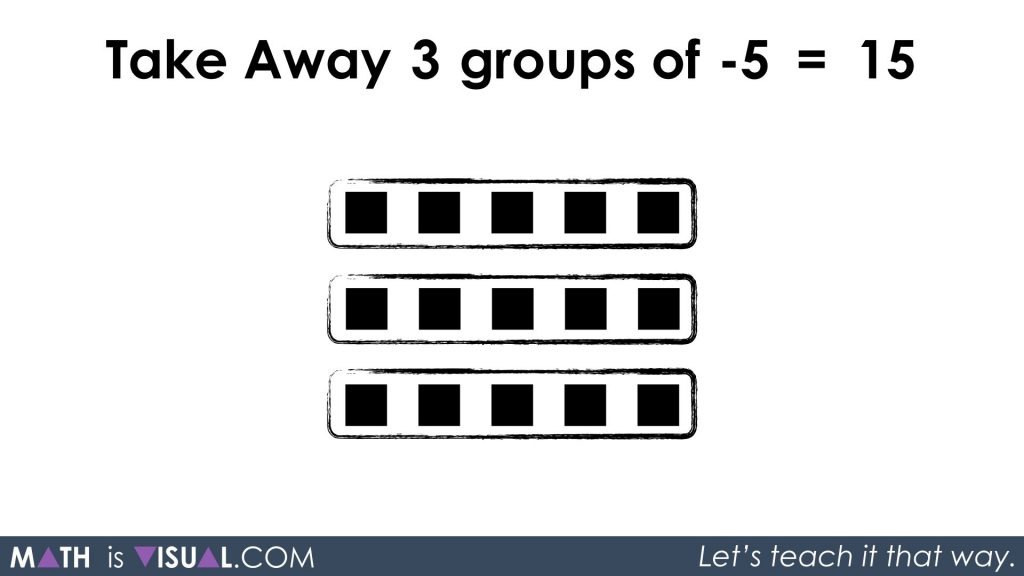
We can write this using symbolic notation as:
-3 x (-5) = 15
or
-(3 x (-15)) = 15
In either case, we are utilizing the zero principle and then removing 15 negative (red) squares and leaving the 15 positive (black) squares.
There you have it again…
Math IS Visual. Let’s teach it that way.




Add comment