Here’s another post to add to the integer operation series. Here, we look at multiplying positive by positive, negative by positive, positive by negative and negative by negative to help students generate their own rules for integer multiplication beginning with the symbolic expressions.
See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.
Visual Prompt #1
In the video above, we start with whole number multiplication as a low floor start:
3 x 2 = 6
3 groups of 2 = 6
The viewer should be comfortable with multiplying and representing multiplication with arrays in order to do this entire activity:

Visual Prompt #2
In the second visual prompt, pause the video at this frame where the viewers are given an opportunity to again show their understanding of multiplication using arrays and number lines:
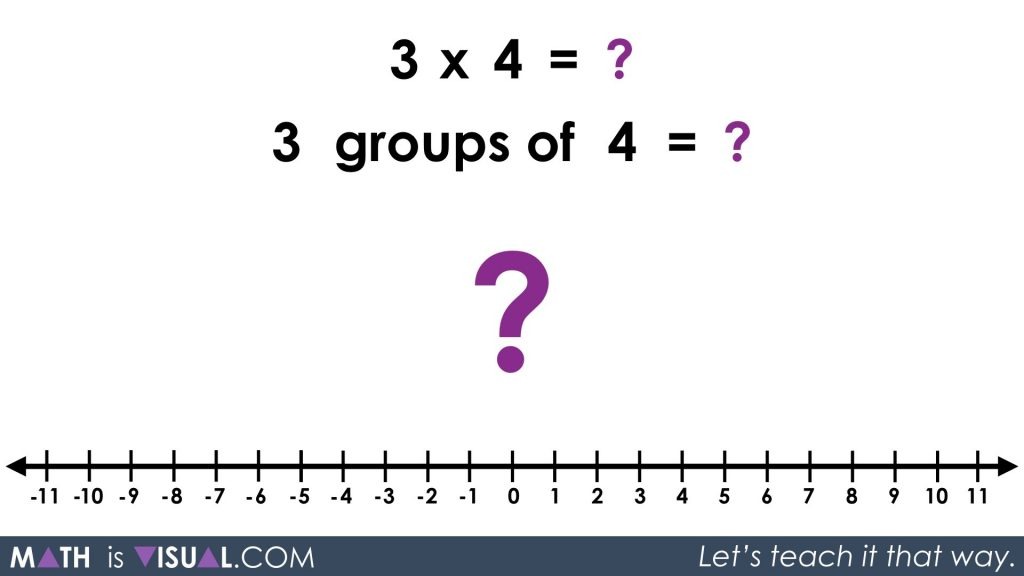
The following frames animate the solution:

Visual Prompt #3
Now we ask the viewer to show what 4 groups of (-2) looks like.

4 groups of (-2) should yield a result of -8:
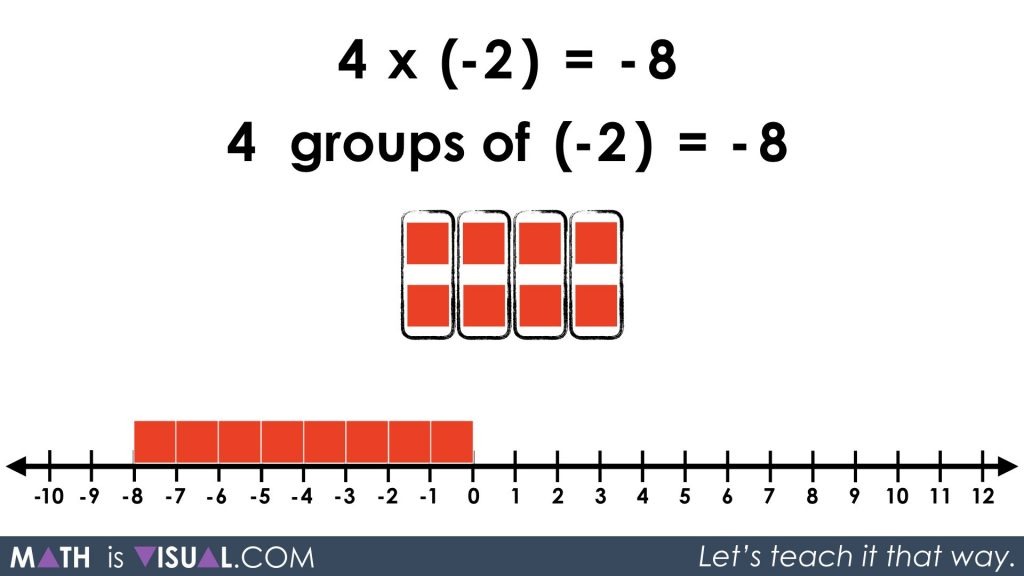
Visual Prompt #4
Viewers are then given another opportunity to work with multiplying a positive by a negative:
3 groups of (-3) = ?

Then, you can show the animated solution:
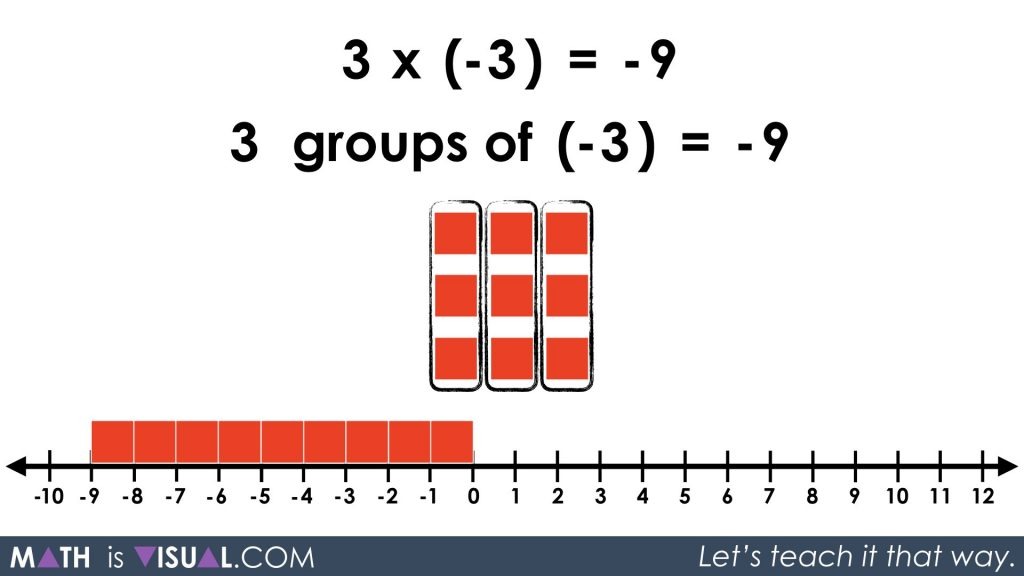
Visual Prompt #5
Now, present the viewer with an opportunity to tinker with what negative groups means:
-2 x 5 = ?
The goal here is for students to gain an understanding that -2 x 5 is the same as subtracting 2 groups of 5.
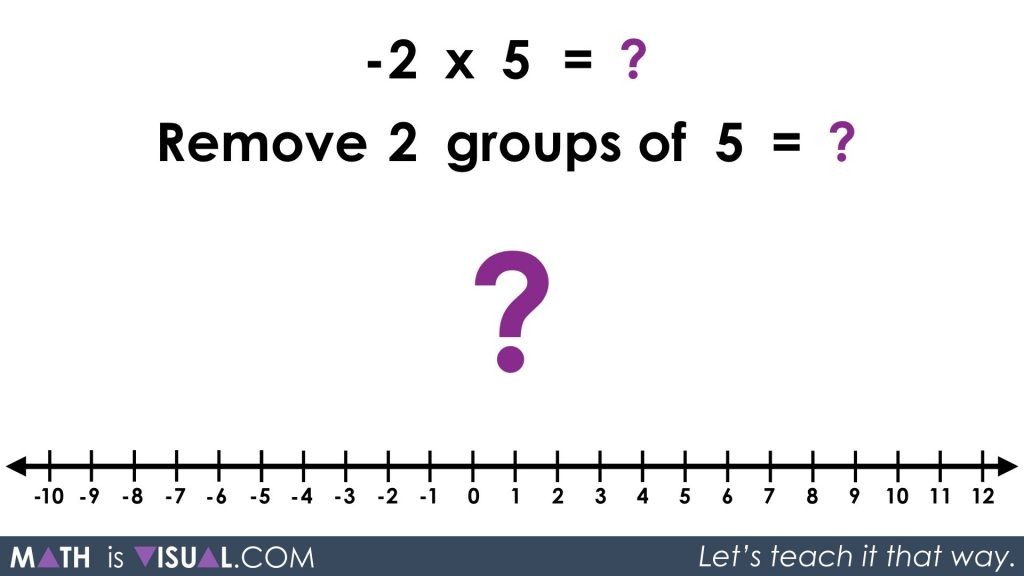
In order to take away 2 groups of 5, we must employ the zero principle (i.e.: 1 + (-1) = 0, so introduce 2 groups of 5 zero pairs). Then, we’ll take away the 2 groups of 5 and be left with 2 groups of -5 or -10:
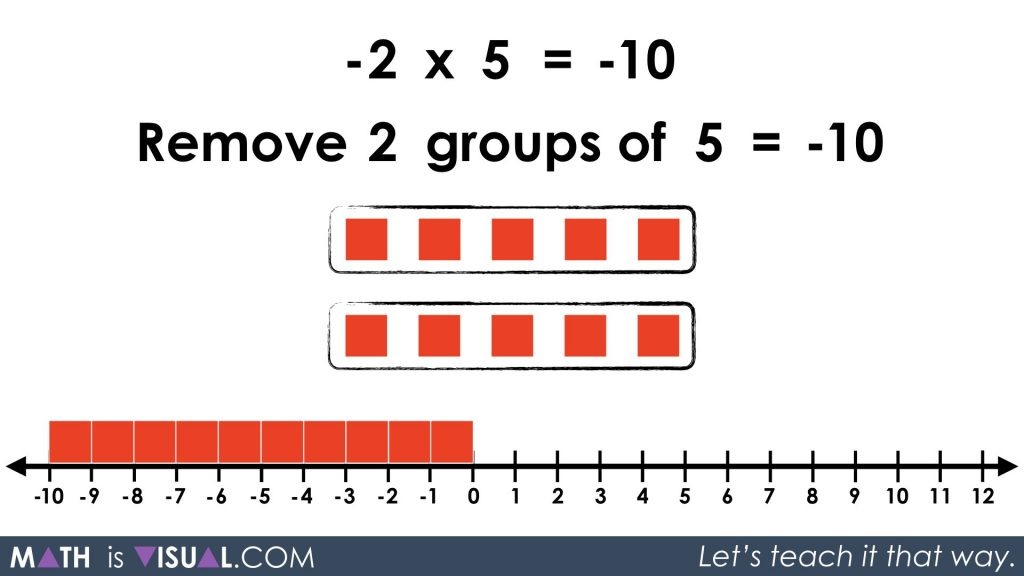
Visual Prompt #6
Here’s another opportunity for the viewer to tinker with this idea:
-3 x 4 = ?
Remove 3 groups of 4 = ?
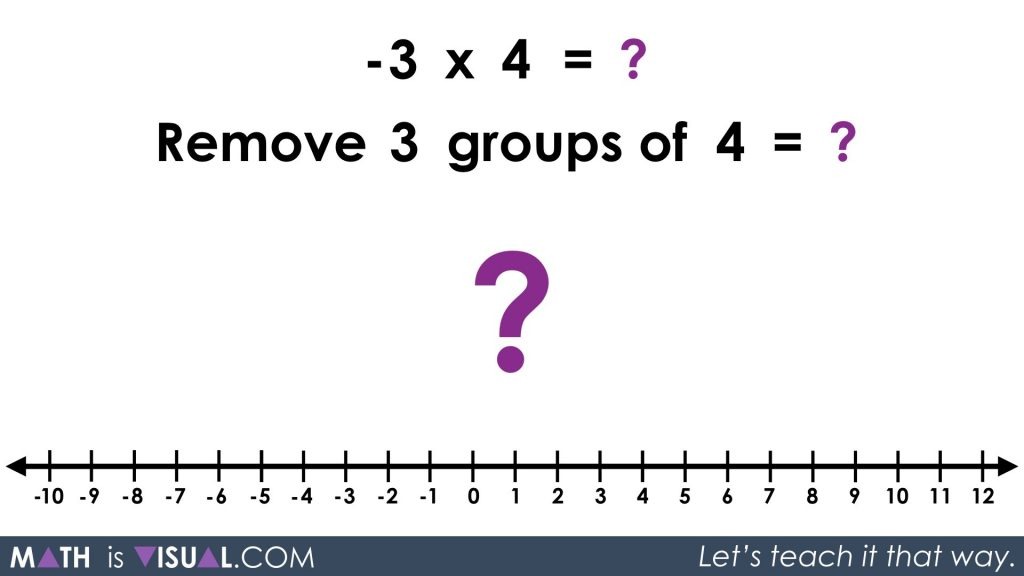
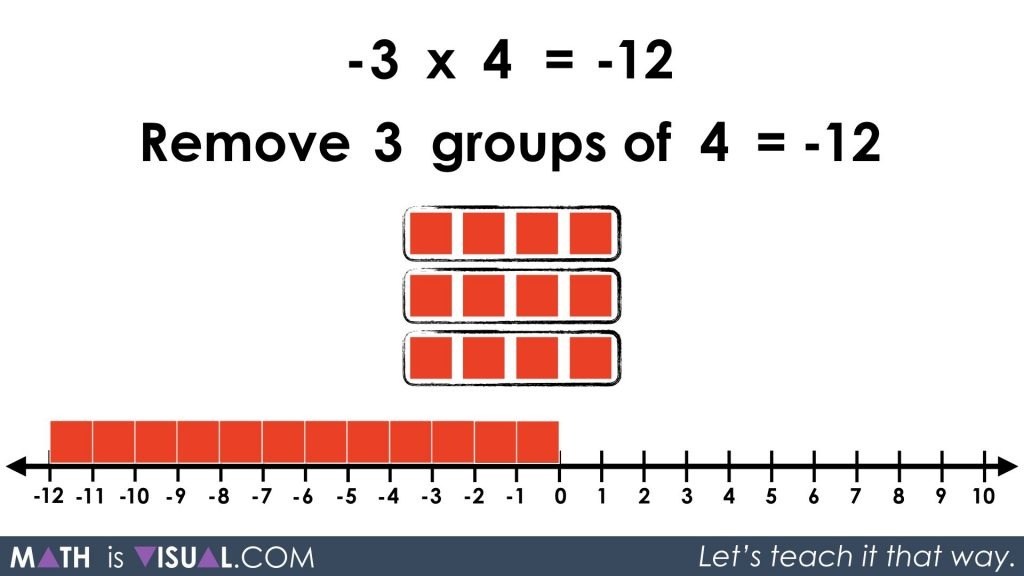
The video animates the solution to show that -3 x 4 = -12:
Visual Prompt #7
Then, we move on to the least intuitive of them all. Multiplying a negative by a negative:
-2 x (-3) = ?
Remove 2 groups of (-3) = ?
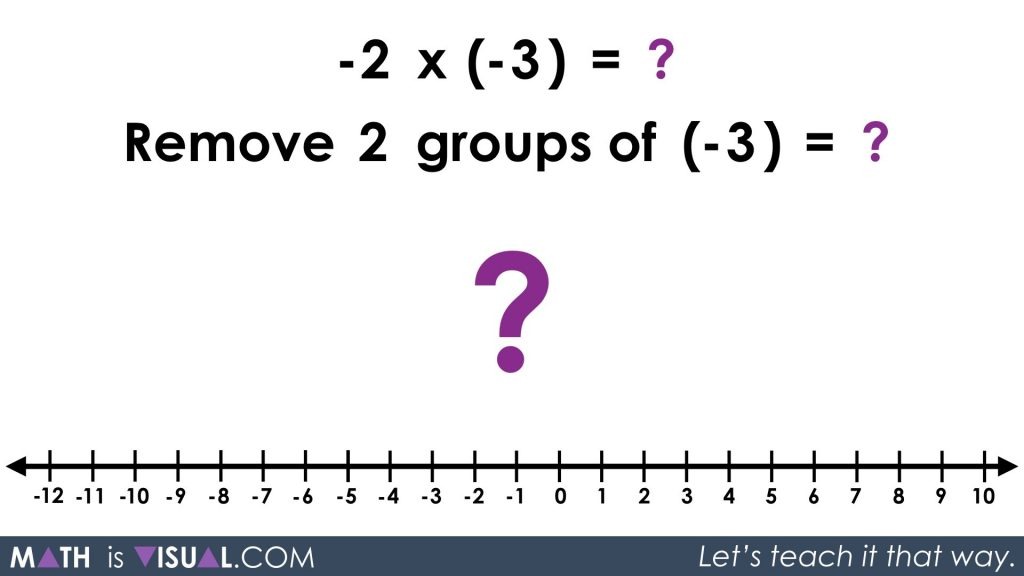
Again, we will use the zero principle, except this time we are removing 2 groups of -3 which will leave 2 groups of positive 3 or 6.

Visual Prompt #8
Finally, the viewer is given an opportunity to try multiplying a negative by a negative to drive home the point:
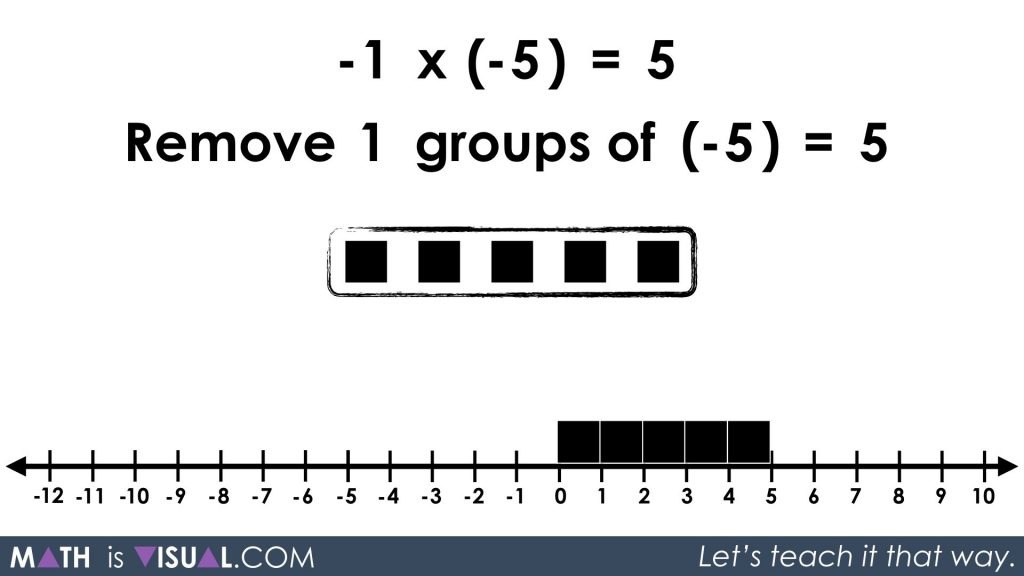
-1 x (-5) = ?
Remove 1 groups of (-5) = ?
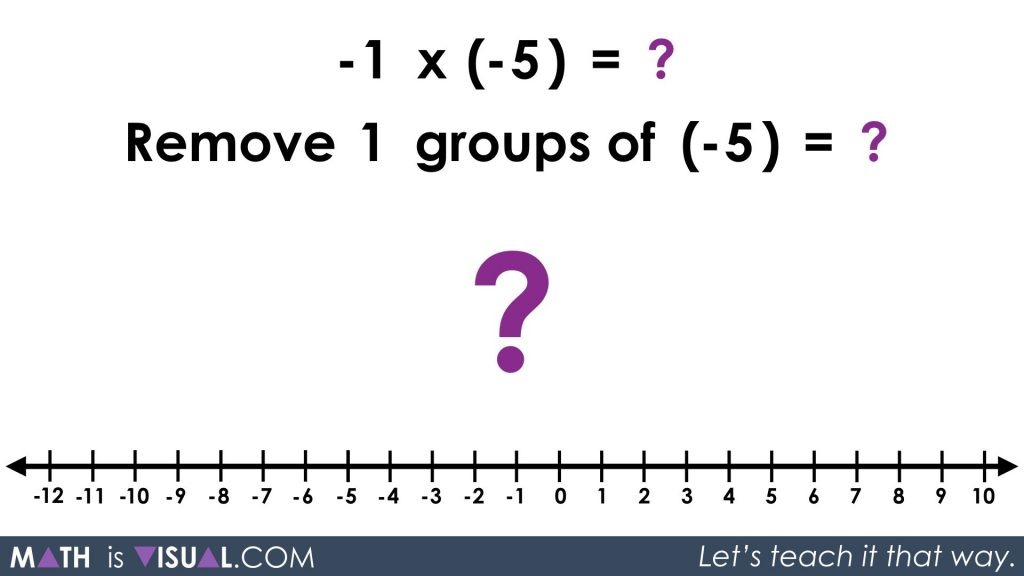
Using the zero principle, we will introduce 1 group of 5 zero pairs in order to remove 1 group of (-5) which will leave 1 group of (+5).
Math IS Visual. Let’s teach it that way.




[…] Visualizing Integer Multiplication […]
[…] Visualizing Integer Multiplication […]