Exploring Two Ways To Think of Ratios

In This Set of Math Visual Prompts…

Students will compare and contrast composed unit ratios to reveal a rate and multiplicative comparison ratios to reveal scale factors through quotative division.

Intentionality…

This set of visual math talk prompts is taken from the Math Talk section of Day 5 in the Make Math Moments Problem Based Unit called Planting Flowers. The purpose of the Math Talk is to reinforce key concepts and big ideas from the first day of this problem based math unit including: 

• There are two types of ratios; composed unit and multiplicative comparison;
• A composed unit is often (not always) a ratio with two distinct units; 
• A composed unit can be scaled in tandem; 
• Equivalent ratios are derived from the same rate; 
• When you divide a composed unit through partitive division, you reveal a rate. 
• A multiplicative comparison is a ratio with the same unit; 
• The scale factor between a multiplicative comparison can be revealed through quotative division. 

This set of visual math talk prompts, we will explicitly compare how the type of ratio can dictate the type of division that students are using to reveal a rate (partitive division) or a scale factor (quotative division).

Preparing to Facilitate

In today’s visual math talk, present the following ratio which is taken from the 5th day of the Make Math Moments problem based unit called Planting Flowers. For each ratio in the string of related problems, we ask students to share an example of a composed unit and a multiplicative comparison. Prompt students to add the appropriate units for each context. For the composed unit examples, ask students to divide the quantities using partitive division to reveal a rate. For the multiplicative comparison examples, ask students to divide the quantities using quotative division to reveal a scale factor. Then, compare and contrast the two scenarios for each set of ratios.

In this visual math talk, we’ll be sharing the first ratio from the string:

75 : 15

An example of a context that might be considered for thinking of these ratios as a composed unit might be a gardener who has 75 seeds to plant and 15 pots. How many seeds per pot can the gardener plant? An example of a context that might be considered for thinking of these ratios as a multiplicative comparison might be a gardener who has 75 seeds to plant and wants to plant 15 seeds per pot. How many pots will the gardener need? In other words, how many groups of 15 seeds are in 75 seeds? 

This string of related problems should be led by the facilitator on a chalkboard/whiteboard/tablet to model student thinking “in the moment”, however you might consider to also leverage the visual math talk clips included below for each problem in the string.

You can learn more about rates, ratios and the roadmap to proportional relationships through the course: The Concept Holding Your Students Back.

Problem #1: 75 to 15 as a Composed Unit

In the first problem from the string, students are asked:

Create an example of a composed unit for the ratio 75:15. Then, use a model to reveal a rate.

As always, value the voice of your students and do your best to model their thinking. While the context that students create for this composed unit ratio of 75:15, similar strategies may emerge such as using a fair sharing strategy to distribute 75 of a quantity into 15 groups (seeds to planter pots, goals to games played, etc.). 

If students do not leverage any linear models, make an attempt to take their thinking and represent it using stacked bar models and/or a double number line then ask them if they can see their thinking in that model.

Helping students to see value in a linear model – like the double number line for example – can be helpful for them to build their multiplicative thinking skills.

Some students may quickly realize that there are 3 groups of 5 in 15, and therefore we could partition the number line into thirds to help reveal how many seeds 5 planter pots would receive.

By scaling the composed unit in tandem like we see above, students are now working with a more manageable equivalent ratio of 25:5. Partitioning that portion of the number line into fifths will allow us to reveal the ratio of number of seeds to 1 pot or a rate of 5 seeds per pot. 

Alternatively, some students may jump straight to using partitive division on 75 seeds and 15 pots to reveal the rate of 5 seeds per pot (or 5 seeds/pot).

Problem #2: 75 to 15 as a Multiplicative Comparison

In the second problem from the string, students are asked to think of the ratio 75:15 as a multiplicative comparison:

Create an example of a multiplicative comparison for the ratio 75:15. Then, use a model to reveal a scale factor.

Again, value the voice of your students and do your best to model their thinking. By this point in our problem based unit on ratios and rates, we hope that students will know and understand that the context they used for a composed unit in the previous problem will not suffice as a multiplicative comparison. When thinking of 75:15 as a multiplicative comparison, we are thinking about this ratio quotatively. In other words, we are wondering “how many 15s are in 75” or visa versa “what fraction of 75 is 15?”

One possible strategy and model might be to stack bars in order to visually compare how much larger (or smaller) one quantity is than the other.

Observe and listen for students thinking additively (i.e.: 75 seeds is 60 seeds greater than 15 seeds) vs. multiplicatively (i.e.: 75 seeds is 5 times greater than 15 seeds).

Note that while students will likely prefer to reveal a scale factor of 5 (i.e.: 75 seeds is 5 times larger than 15 seeds), be sure to highlight the reciprocal scale factor (i.e.: 15 seeds is 1 fifth times as great as 75 seeds).

It is worthwhile to leverage student thinking from stacking bars to connect to a double number line. If student thinking is shared in a vertical fashion, you might consider creating a vertical number line. The same is true if students are sharing thinking in a horizontal fashion. 

By emerging a double number line, the idea of equivalent ratios can be quickly revealed. For example, from the double number line, we can see that 75:15 is equivalent to x:1.

Avoid rushing to an algorithm and rather promote reasoning for students to determine what the missing scale factor would be in this case. This means we are not setting up a proportion and solving using cross multiplication.

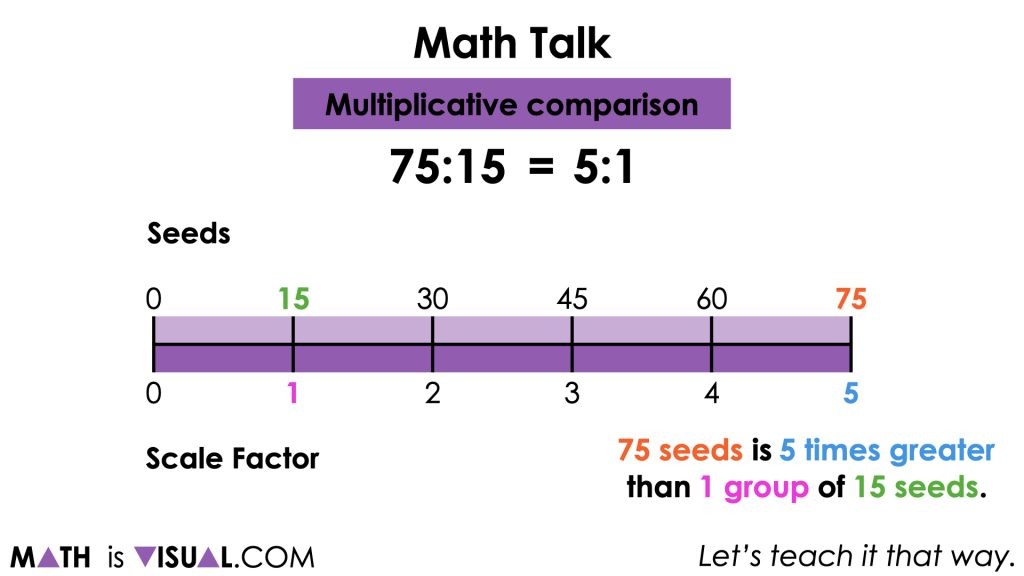
While it might seem easier to see that 75 seeds is 5 times larger than 15 seeds, it is also worth noting that if our unit is 75 seeds, that 15 seeds is 1 fifth of that amount.

Encourage students to explore the behaviours of the two types of ratios (composed units and multiplicative comparisons) on the double number line and you might be surprised what procedures they highlight.

Want to Explore These Concepts & Skills Further?

Two additional visual math talk prompts are available in the Day 5 Math Talk section of Planting Flowers problem based math unit. 

Why not start from the beginning of this contextual 5-day unit of ratios and rates real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.