Integer Multiplication

Throughout the integer operation series, we have focused only on adding and subtracting integers. Now that students have developed a solid understanding of how integers work, we will continue the series by introducing the multiplication of integers. YES, finally, onto multiplying negative and positive values as many have requested to date.

The video shown at the top of the post has the entire visual progression of integer multiplication as described below in the visual prompts.

See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.

Visual Prompts: Question 1, Act 1

The beginning of the video prompts the viewer with this visual:

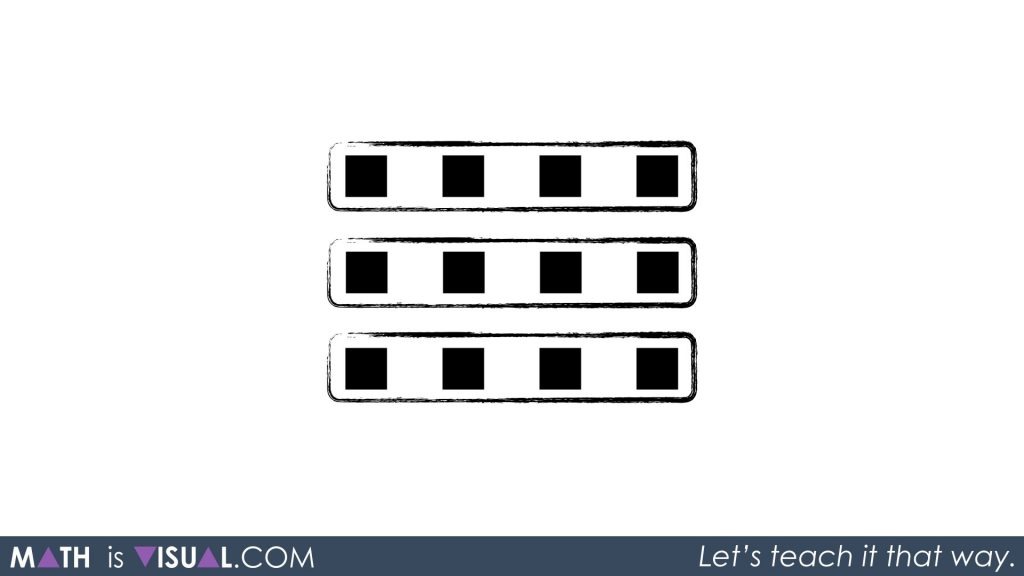
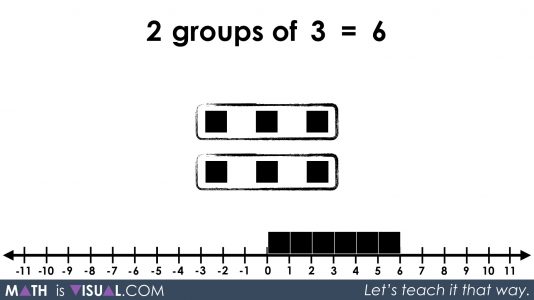
Here were are trying to help the viewer “see” the 3 groups of 4 black squares. In previous videos, we represented the black squares as positive integers. Thus we are looking for the viewer to be able to say and possibly write:

3 groups of 4

or

3 x 4

Since I’m sure students who are multiplying integers are comfortable with multiplying 3 x 4, we give this result immediately as 12 and show it on the number line.

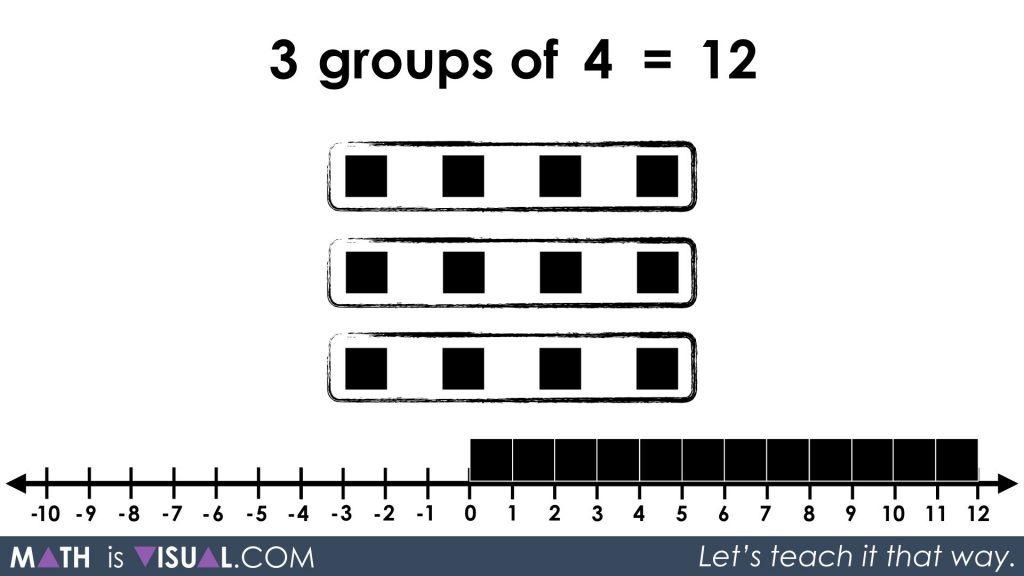
We also show that we can rearrange our groupings to be:

4 groups of 3

or

4 x 3

 

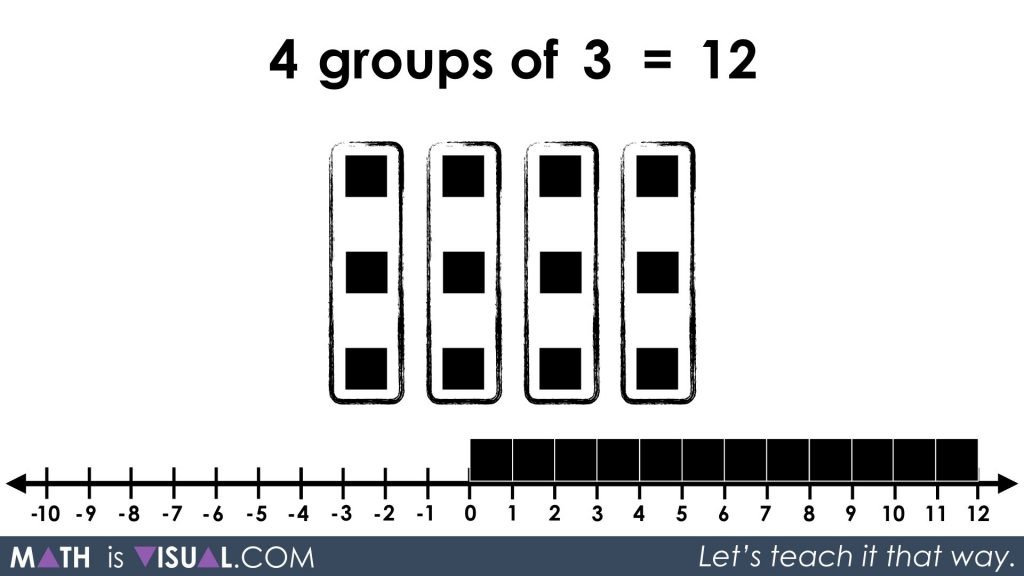
Easy stuff so far.

Multiplying a Positive By a Negative

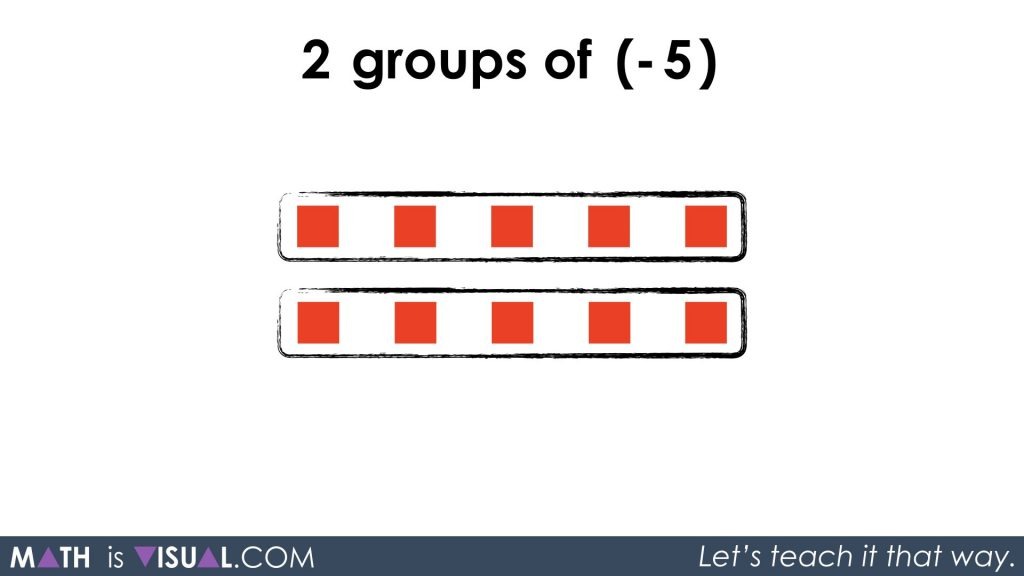
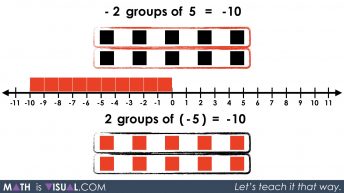
Now, we introduce the following visual:

As the viewer should recall, the red squares represent negative values in our series. Therefore, we want the student to identify this visual as:

2 groups of (-5)

or

2 x (-5)

By simply using the same skills developed on the adding and subtracting integers series, we can easily arrive at a simplified result of -10.

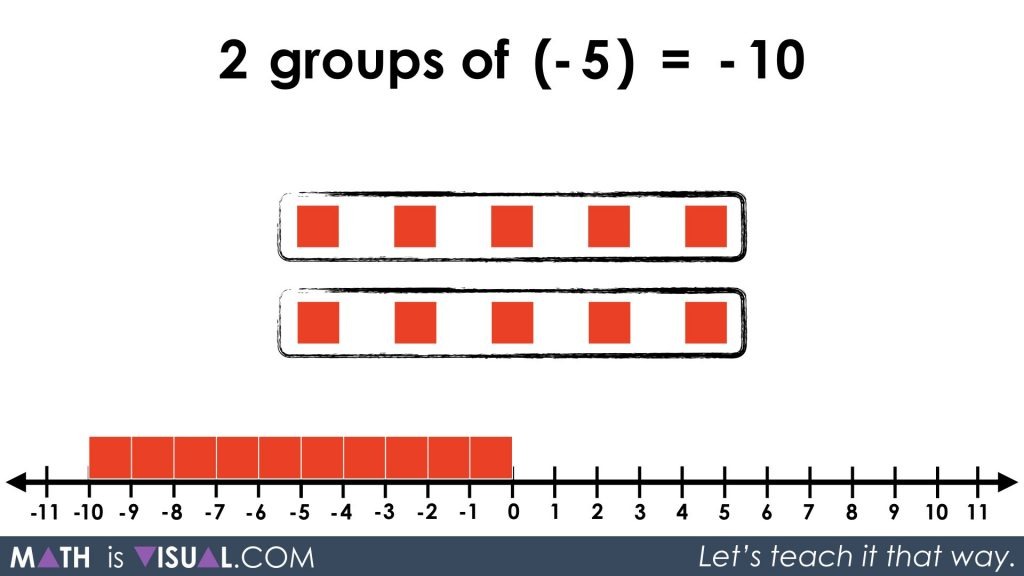
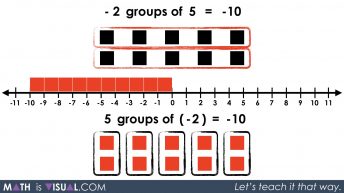
We note that 2 groups of (-5) is the same as 5 groups of (-2).

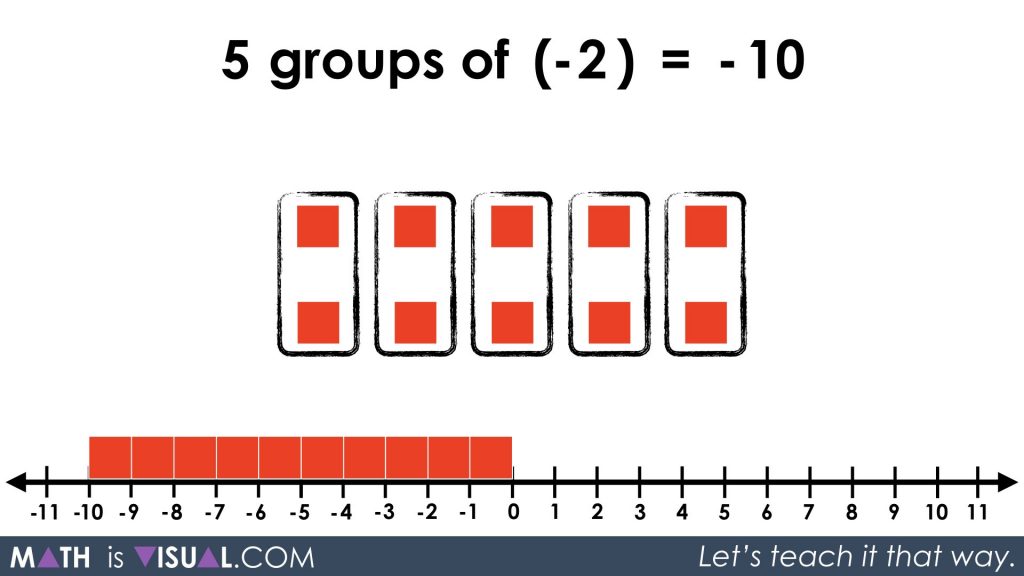
We then show students the different possible products that result in -10 really focusing on driving home the idea that positive and negative values are intrinsically related and are inverse values on the number line.

Multiplying a Negative By a Positive

Then, we move onto a prompt where our squares are positive (black) and our groups are negative.

Hoping students will come up with:

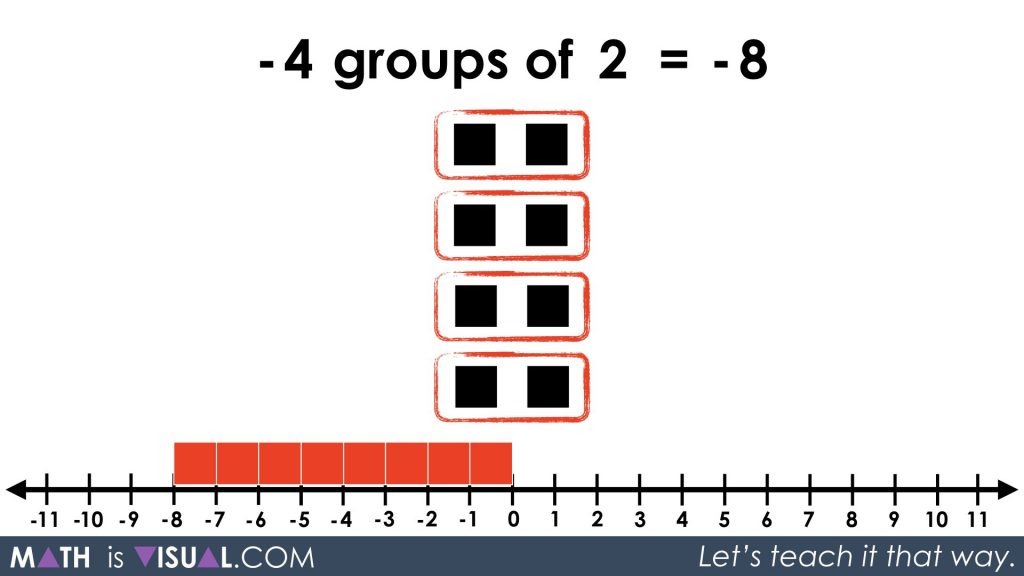
-4 groups of 2

or

-4 x 2

or similar

While this is less intuitive, leaning on our prior understanding from earlier in the video, one might argue that if we ignore the colour of the squares (i.e.: the absolute value), we recognize that the result will involve 8 squares.

However, which colour will they be?

If we know:

4 groups of 2 = 8

and

4 groups of -2 = -8

then, a student might conjecture that

-4 groups of 2 = -8

I’m curious to hear feedback around this one to learn what the majority of students think. Please do let me know in the comments!

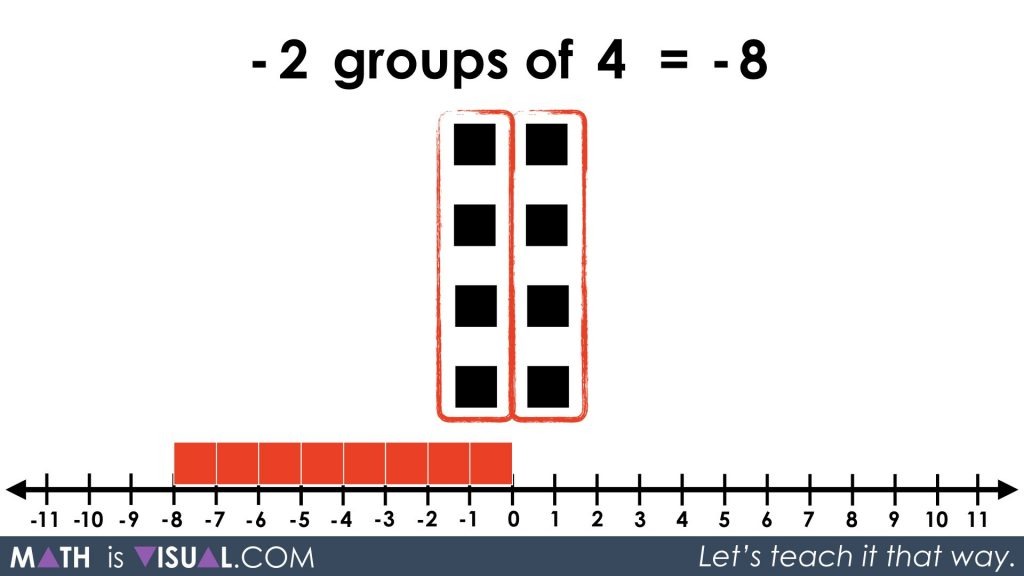
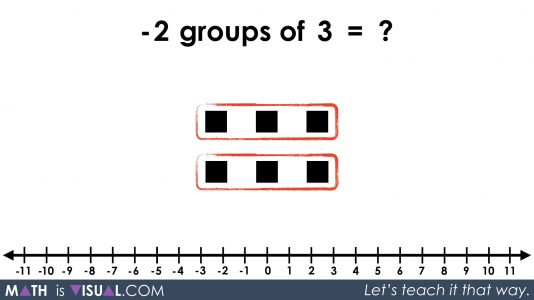
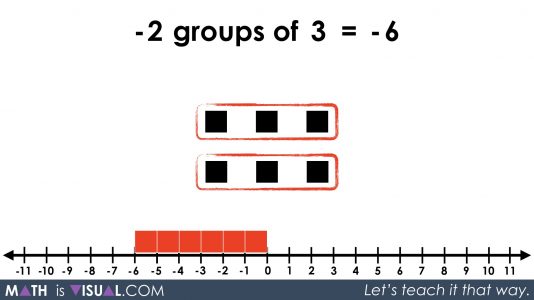
From what we’ve learned earlier, it would make sense that -2 groups of 4 also equals -8:

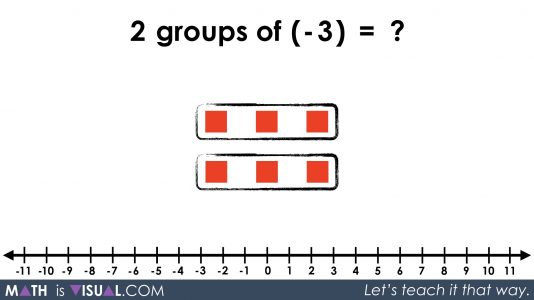
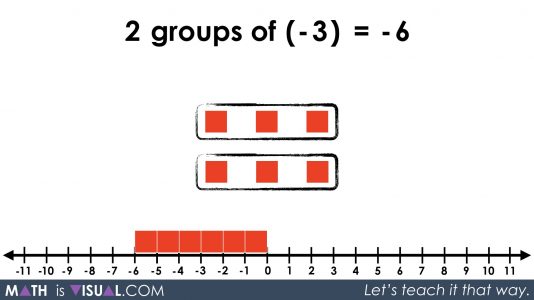
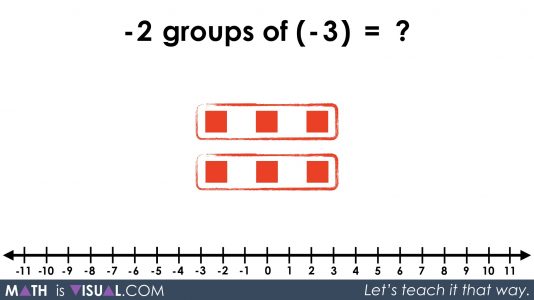
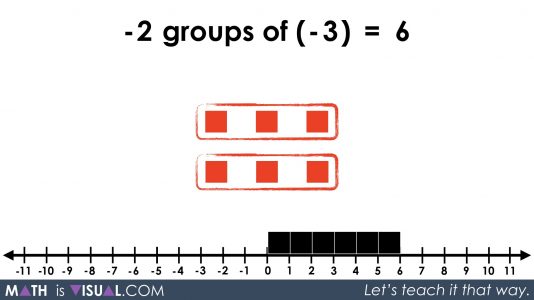
Multiplying a Negative By a Negative

Using this intrinsic relationship between positive and negative values, we now head to multiplying a negative by a negative showing both a negative number of groups and negative values in those groups:

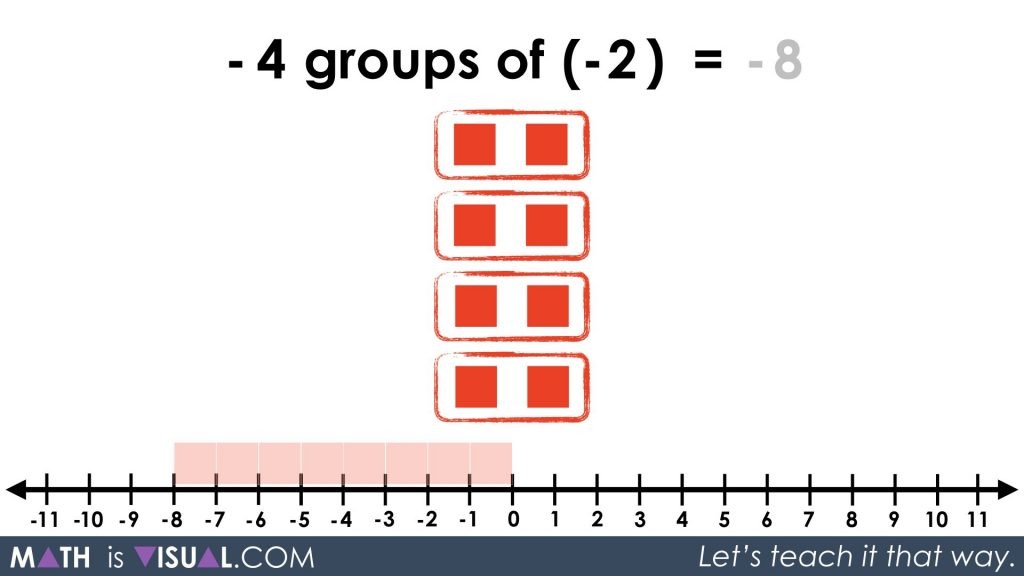
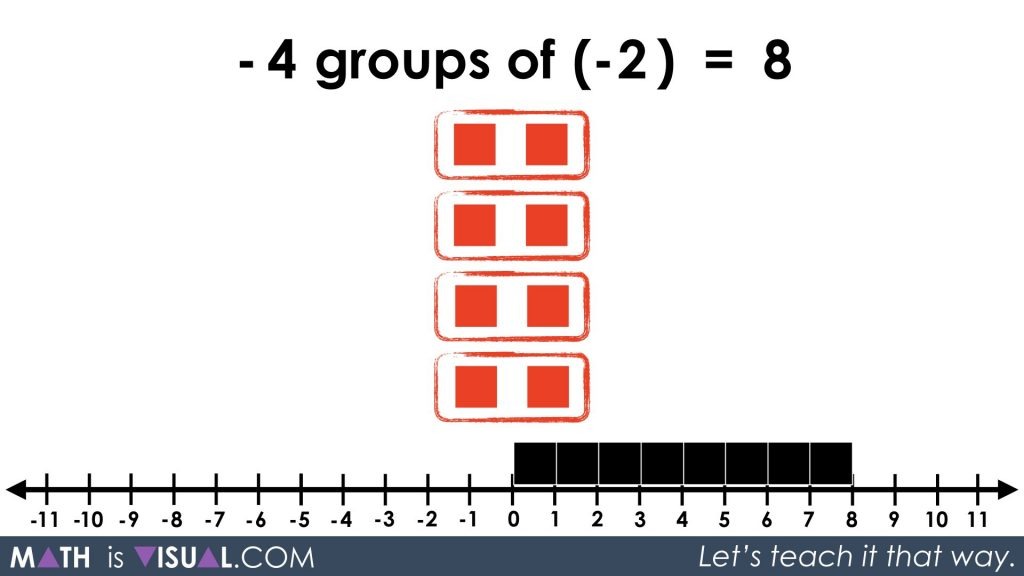
This is really hard to understand, but with all the work we did above multiplying positive by a positive and positives with negatives, hopefully the logic can follow.

A contextual idea we might consider is from language where double negatives result in a positive. Here is an example:

It is not going to not rain today.

Wow, that sounds ugly.

However, if we really think about this, both negatives cancel out here and that sentence suggests it will in fact rain today.

Something similar is taking place with our multiplying a negative by a negative.

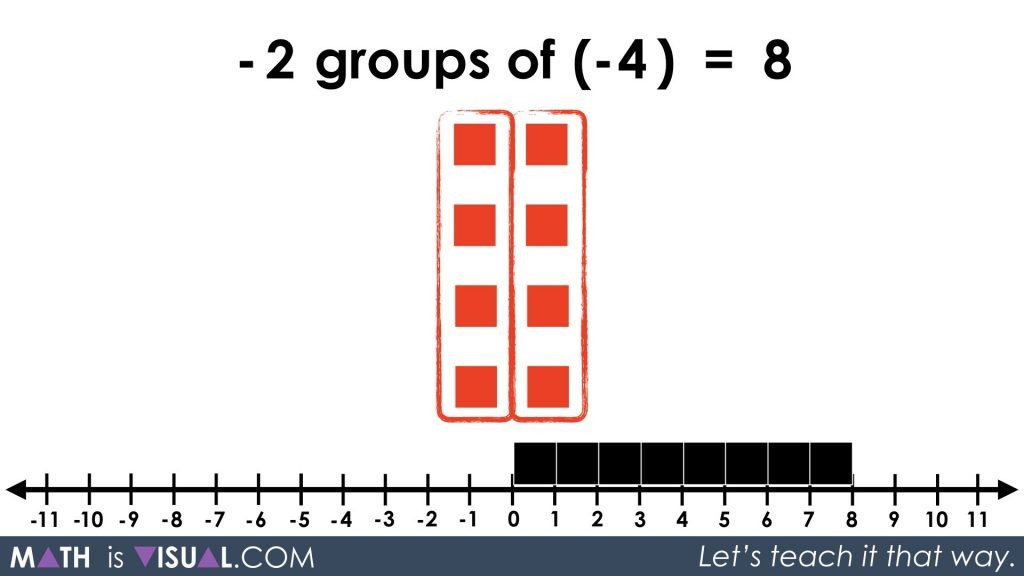
We can also show students that we can rearrange our groupings and come up with the same result:

Visual Prompts for Multiplying Integers

Finally, here are a few practice prompts you might consider using after exploring the beginning of this post: