Subtracting Positive and Negative Integers – Part 3

In this visualization video, we re-introduce the zero principle to subtracting positive and negative integers.

By showing black and red squares combining and disappearing as well as black and red squares re-appearing in an attempt to show that we can add more squares of one colour as long as we add the same amount of the other colour as well.

Following the introductory revisiting of the zero principle, we introduce the problem:

7 black squares take away 2 red squares

As you can imagine, this is problematic for students as there are no red squares to take away!

What must we do?

If we recall the introduction showing that a black and red square can combine to disappear and also can “re-appear” when we want them to, we could simply add 2 red squares (so we can take them away) and 2 black squares.

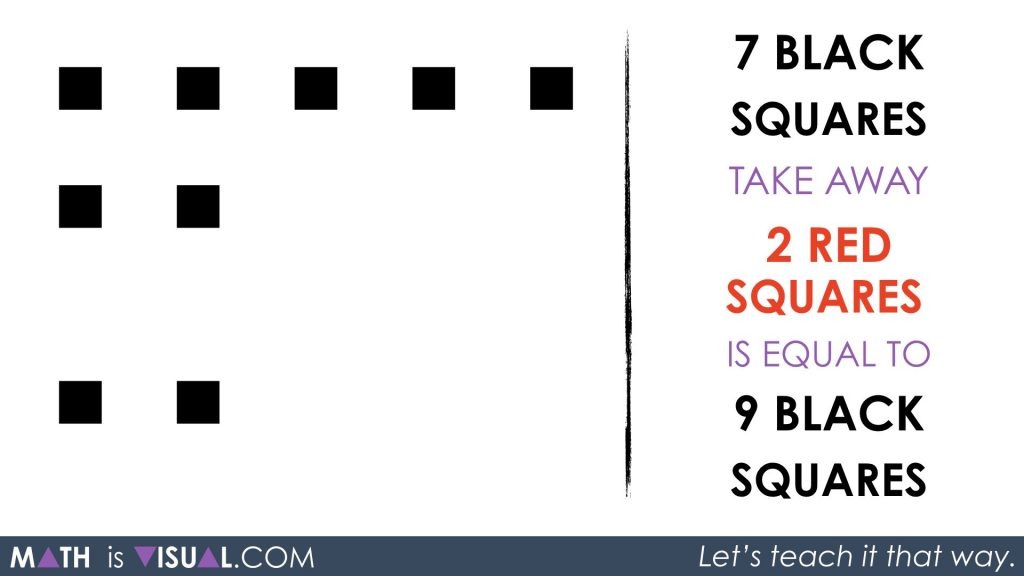
Now, we replace the words with the math symbolic representation as well as re-arrange the squares to look a bit more “pretty” and easier to subitize:

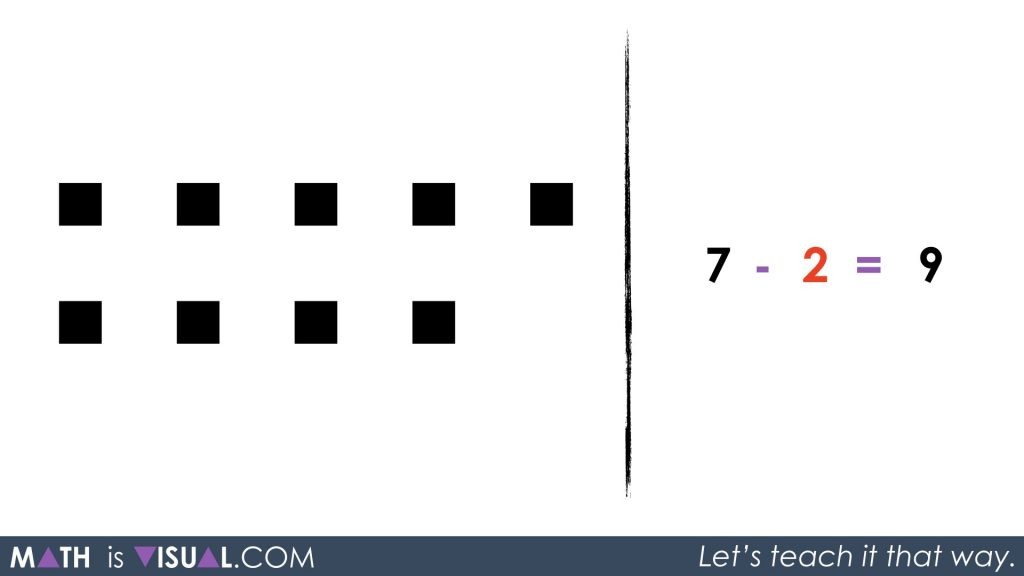
Math Is Visual Prompts

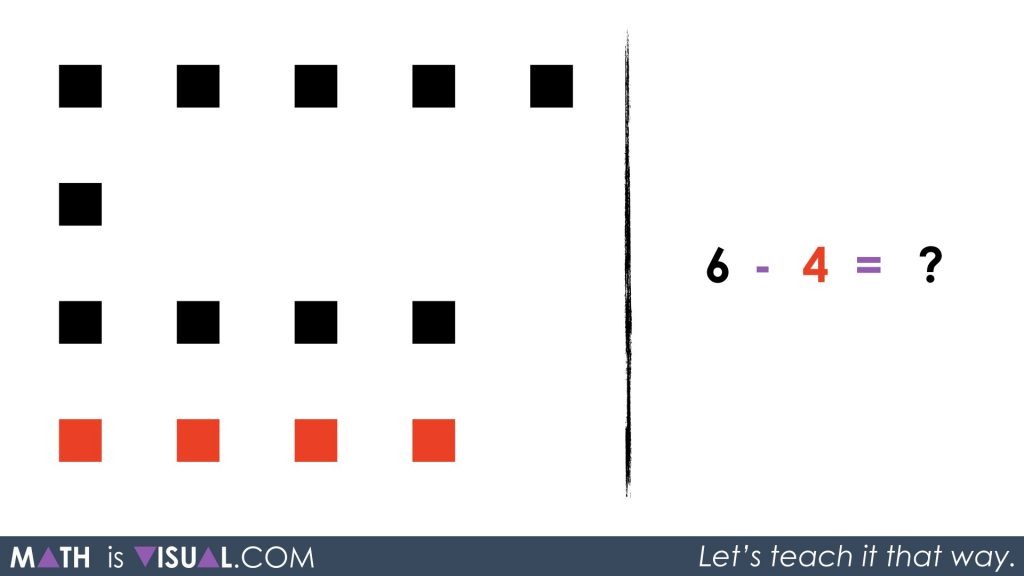
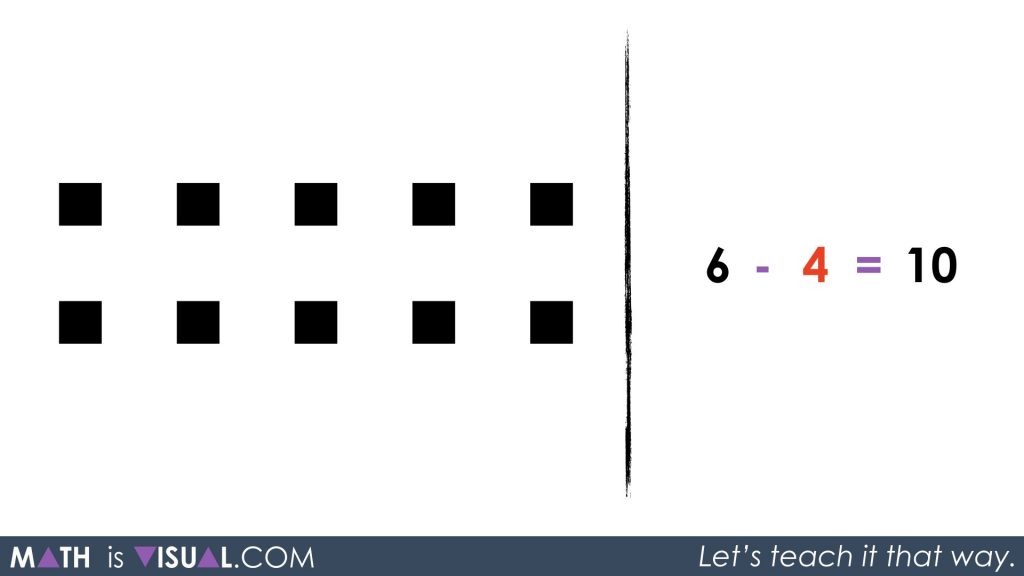
Students are then given the following symbolically to represent concretely and then symbolically, on their own:

6 black – 4 red = ?

Check out the animated video here:

You can also consider using the following visual prompt images below:

It might be worth reviewing the initial video to ensure that students are picking up on the “rules” of the zero principle. Here is the initial video again, to avoid having to scroll up:

Hopefully, students will recognize that by using the zero principle, we can make 4 red squares appear as long as we also make 4 black squares appear.

Then, students can “take away” or subtract the 4 red squares and will be left with 10 black.

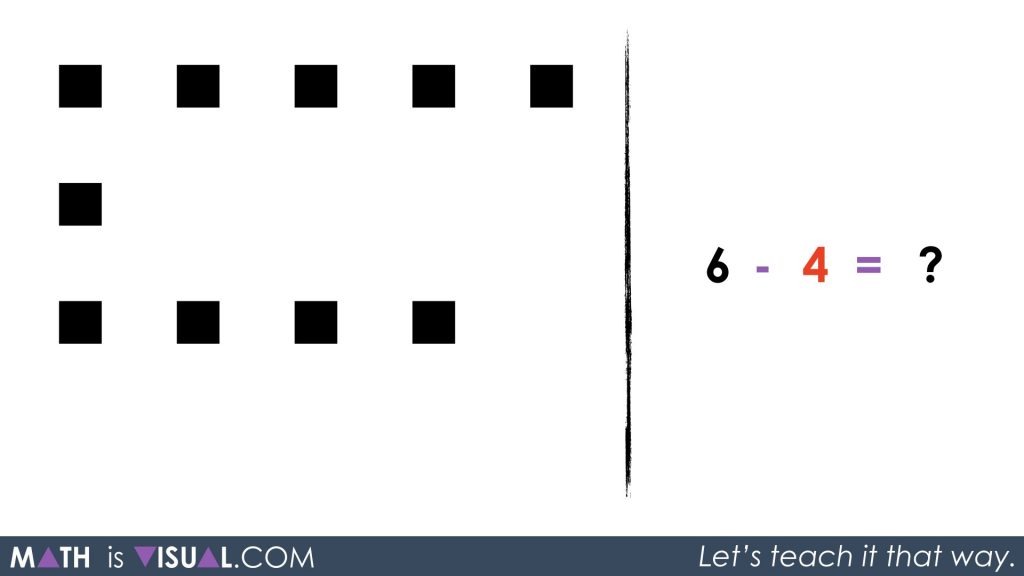
Rearranging the squares might make conceptually subitizing the total a bit easier.

Hope you and your students enjoy this exploration.

Math is visual. Let’s teach it that way!