How to Find the Circumference of a Circle Using Pi, π

In This Set of Math Visual Prompts…

Students will apply the relationship between circumference and diameter of a circle known as Pi to find the unknown circumference given the diameter of a circle.

Intentionality…

This set of visual number talk prompts is taken from the Number Talk section of Day 3 in the Make Math Moments Problem Based Unit called Going In Circles! The purpose of this Visual Number Talk is to reinforce key concepts and big ideas from this problem based math unit including:

• When exploring measurement relationships of any circle, there are three (3) standard measures that can be used to reveal more information about the circle:
  • Circumference: the perimeter of a circle.
  • Diameter: any straight line segment beginning and ending on the outer edge of a circle and passes through its centre.
  • Radius: any straight line segment beginning at the centre of a circle and ending on the outer edge of the circle.
• Knowing one of the standard measures of a circle provides information about all other measures;
• There is a multiplicative relationship between the length of the diameter and the circumference of a circle. In other words, as the diameter of a circle increases, the circumference increases multiplicatively (not additively);
• For all circles, the ratio of the circumference to the diameter is the same (approximately 22:7); and,
• For all circles, the rate of each unit of circumference length per unit of diameter length is the same (approximately 22/7 or 3.14) and is known as Pi, π.

Want to take a deeper dive into these concepts? Consider starting from the beginning of this 5-day problem based unit.

Preparing to Facilitate This Number Talk

Present the visual number talk prompt by playing the video, pausing where indicated throughout.

The prompts shared with students throughout the video is:

How many units will it take to wrap the circle?

Make an estimate.

Throughout the visual number talk prompts, students will be given an opportunity to build their multiplicative number flexibility by estimating the circumference of different circles beginning with a very small diameter that gradually increases from prompt to prompt. 

Through this work with the approximate 3.14 to 1 ratio between the circumference and the diameter of any circle, students will be encouraged to explore the double number line model or ratio table and apply the use of partial products made possible with the distributive property through the following string of related problems. 

It can be helpful to craft a context that students can leverage throughout this string. For example, using the Tile Circle context from Day 2 could be helpful where each problem is an expression beginning with the multiplicative comparison between the circumference and the diameter (Pi, π) and the diameter in square tiles. 

This number talk can be explored with an animated approach leveraging the visual number talk prompt videos below or in a low-tech fashion by orally sharing with students and writing on a vertical surface like a chalkboard or whiteboard. Regardless of which approach you choose, it is highly encouraged that the facilitator annotate student thinking on a vertical surface such as a chalkboard, whiteboard or projector so students feel their thinking in honoured and worth sharing. 

Five (5) additional visual math talk prompts are shared in the Teacher Guide from Day 3 of the Going In Circles problem based math unit.

Visual Math Talk Prompt #1

Begin playing the video to share the first visual number talk prompt and be ready to pause the video to allow for think time.

The prompt for visual number talk prompt #1 is:

How many units will it take to wrap the circle?

Make an estimate.

Of course, be sure to let students know that you want them to be estimating without the use of a calculator and you want them to craft a convincing argument for how they came up with their estimate. This might include the use of mathematical models such as visual models, symbolic models or even share their thinking orally. 

For some students who have participated in the first two days of this unit, they might recall that we learned the circumference of any circle is about 3 times longer than the diameter; a multiple known as Pi, π. Therefore, some students might be able to quickly estimate an answer of “about 6 units” for the circumference, while others might be able to come up with a more precise estimate given that they know they need approximately an additional 14 hundredths of the diameter. In this case, an additional 14 hundredths of each of the 2 units used to measure the diameter.

It can be helpful to highlight that since a circle with a diameter of 1 unit would have a circumference of approximately 3.14 units, doubling our diameter would also double our circumference. 

It can be helpful to highlight this on a double number line and/or in the ratio table. 

Finally, highlighting that we can write this algebraically as C = πd and multiplying the diameter by a rate of 3.14 circumference units per diameter unit can also be beneficial.

Therefore, 10 cheese slices ÷ 5 crackers results in a rate of 2 cheese slices per cracker.

Visual Math Talk Prompt #2

Continue playing the video for the next Visual Math Talk Prompt.

As students begin making their estimates, be sure to monitor which students are actually leveraging their understanding of Pi, π, which students are leveraging the π to 1 composed unit ratio relationship to scale in tandem (i.e.: doubling the diameter and doubling the circumference from prompt #1) and which students are leveraging rate reasoning to multiply Pi, π as a rate by the diameter.

Regardless of the method students choose, the goal is that all students share an estimate of between 12 and 13 units. 

After modelling student ratio reasoning via scaling in tandem on a double number line and/or ratio table, ensure that you also highlight rate reasoning via leveraging the circumference formula as well.

Visual Math Talk Prompt #3

Continue playing the video for the next Visual Math Talk Prompt.

Continue monitoring what strategy and mathematical model each student is leveraging as they work through this string. Can you encourage them to also show it using another approach?

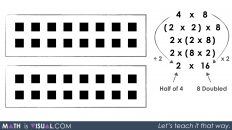
If some students are consistently using a more friendly 3 instead of 3.14 as an approximation for Pi, π, consider modelling the multiplication of 3.14 by 8 units using partial products on the number line and/or with an area model. 

For example, decomposing 3.14 into (3 + 0.14) allows for multiplying 3.14 by 8 units in two parts:

3.14 x 8 units
= (3 + 0.14) x 8 units
= (3 x 8 units) + (0.14 x 8 units)

This may or may not be more helpful for some students as multiplying 0.14 by 8 units might still be a challenge. However, we might leverage a doubling and halving strategy to help us make this calculation more friendly without the use of a calculator:

= (3 x 8 units) + (0.14 x 8 units)
= 24 units + (0.28 x 4 units)
= 24 units + (0.56 x 2 units)
= 24 units + (1.12 units)
= 25.12 units

Want to Explore These Concepts & Skills Further?

Five (5) additional number talk prompts are available in Day 3 of the Going In Circles problem based math unit that you can dive into now. 

Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.