In This Set of Math Visual Prompts…
Students will deepen their understanding and develop their skills related to circumference, radius/diameter and area of a circle.
Intentionality…
Through this purposeful practice, students will apply the concept of circumference and area of a circle to deepen understanding and begin building procedural fluency related to big ideas including the following:
- When exploring measurement relationships of any circle, there are three (3) standard measures that can be used to reveal more information about the circle:
- Circumference: the perimeter of a circle.
- Diameter: any straight line segment beginning and ending on the outer edge of a circle and passes through its centre.
- Radius: any straight line segment beginning at the centre of a circle and ending on the outer edge of the circle.
- Knowing one of the standard measures of a circle provides information about all other measures;
- There is a multiplicative relationship between the length of the diameter and the circumference of a circle. In other words, as the diameter of a circle increases, the circumference increases multiplicatively (not additively);
- For all circles, the ratio of the circumference to the diameter is the same (approximately 22:7); and,
- For all circles, the rate of each unit of circumference length per unit of diameter length is the same (approximately
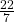or 3.14) and is known as Pi, π. - The area of a circle can be determined by decomposing and recomposing the figure into familiar polygons (i.e.: rectangles or parallelograms); and,
- For all circles, changing the diameter or radius will affect the area and circumference in predictable ways.
Preparing to Facilitate This Number Talk
Visual Math Talk Prompt #1
Begin playing the visual number talk prompt video and be ready to pause the video where indicated to allow for think time.
Share the following prompt both visually on the screen and verbally:
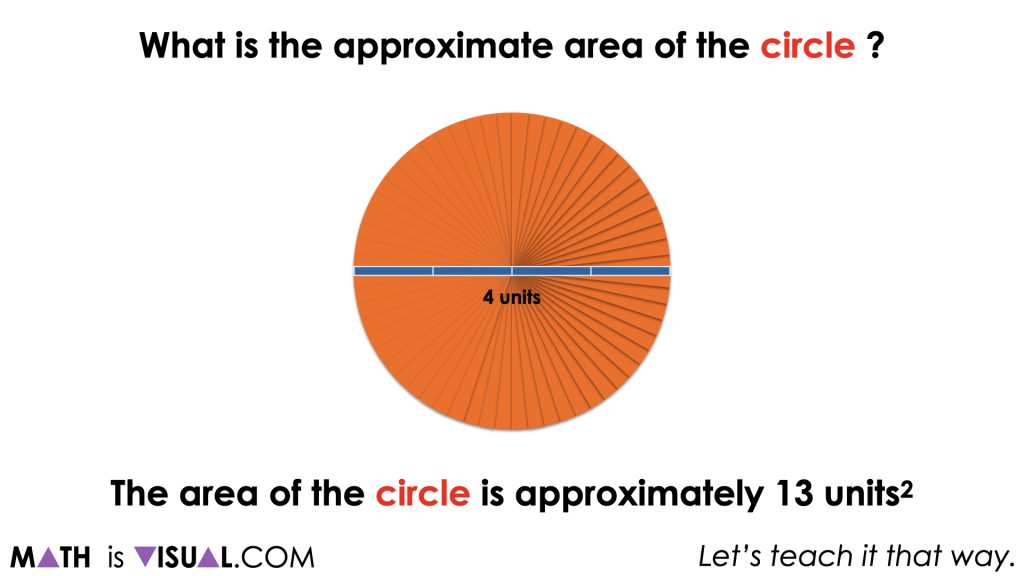
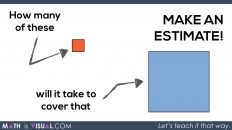
What is the approximate area of a circle with a diameter of 4 units?
Make an estimate.
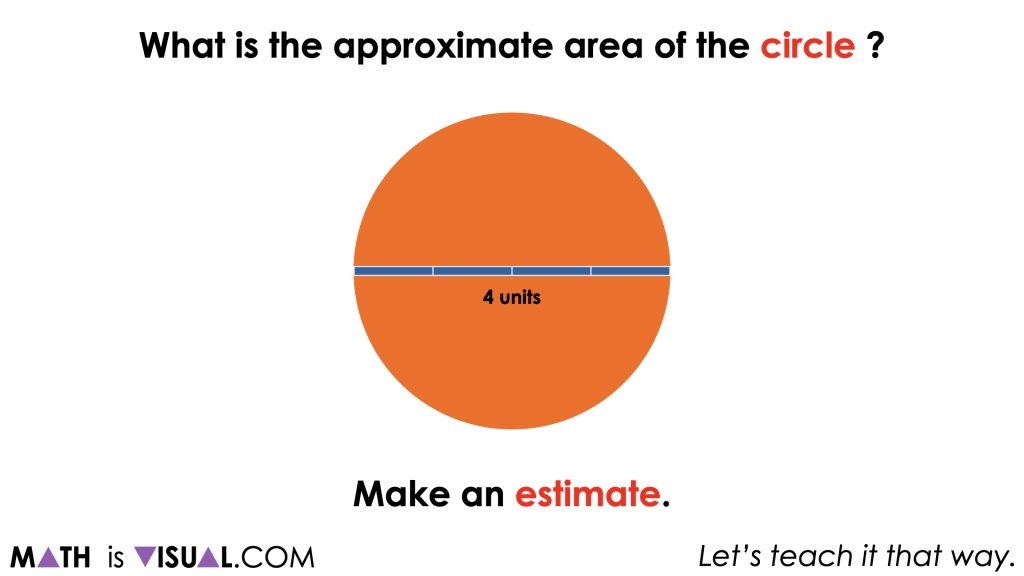
By this point in the unit, the hope is that all students have build fluency and flexibility with the relationship between the length of the circumference and the length of the diameter of any circle and therefore can quickly approximate the circumference to be “a little more than” 3 times the diameter, or about 13 units long.
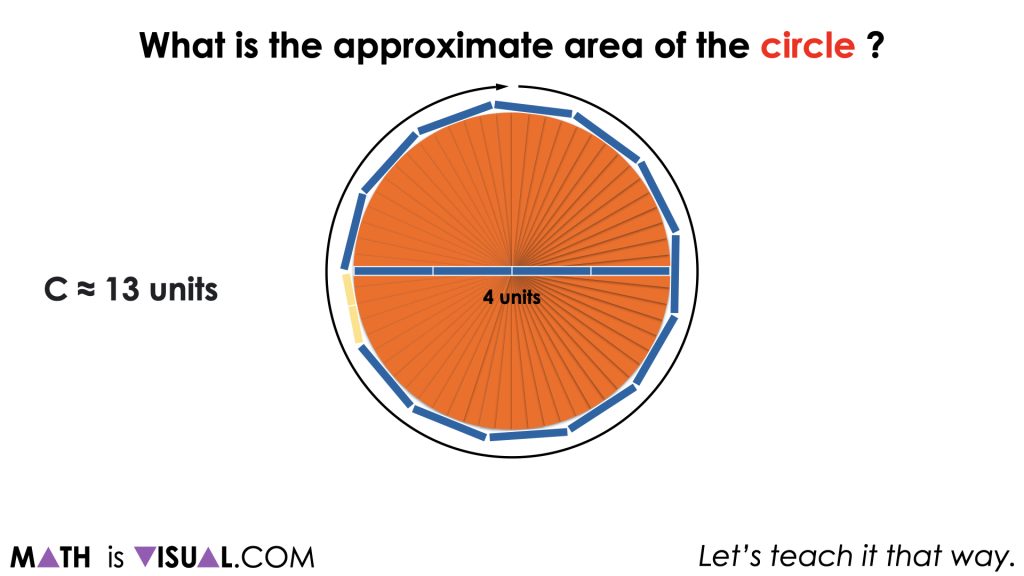
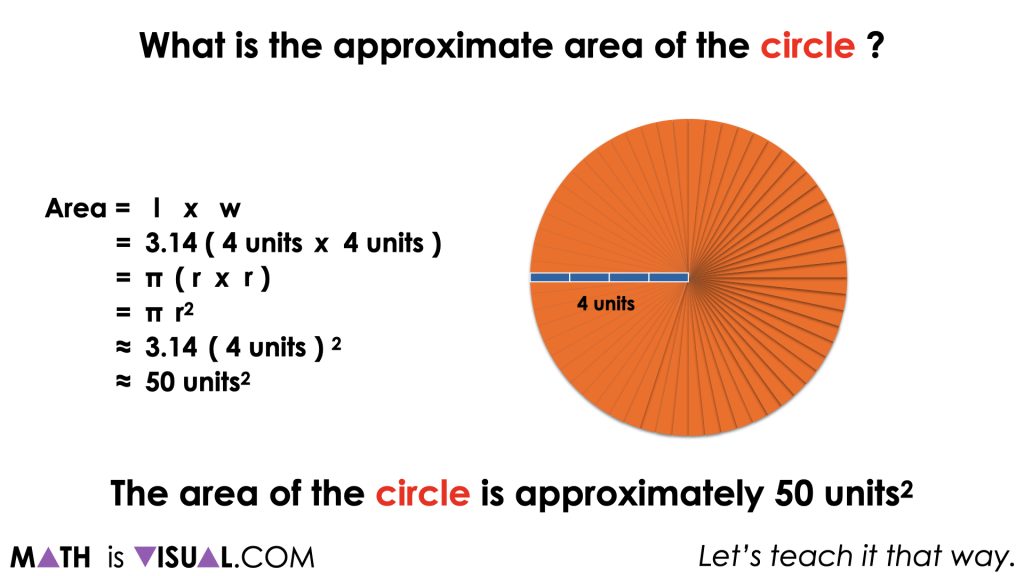
From here, it is likely that you will have some students who want to rush to the algorithm and simply plug in 4 units and π (or about 3.14) into the formula, A = π
, which is fine. However, encourage them to be convincing which will require them to model how the formula is derived by decomposing and recomposing the circle into a more friendly shape.
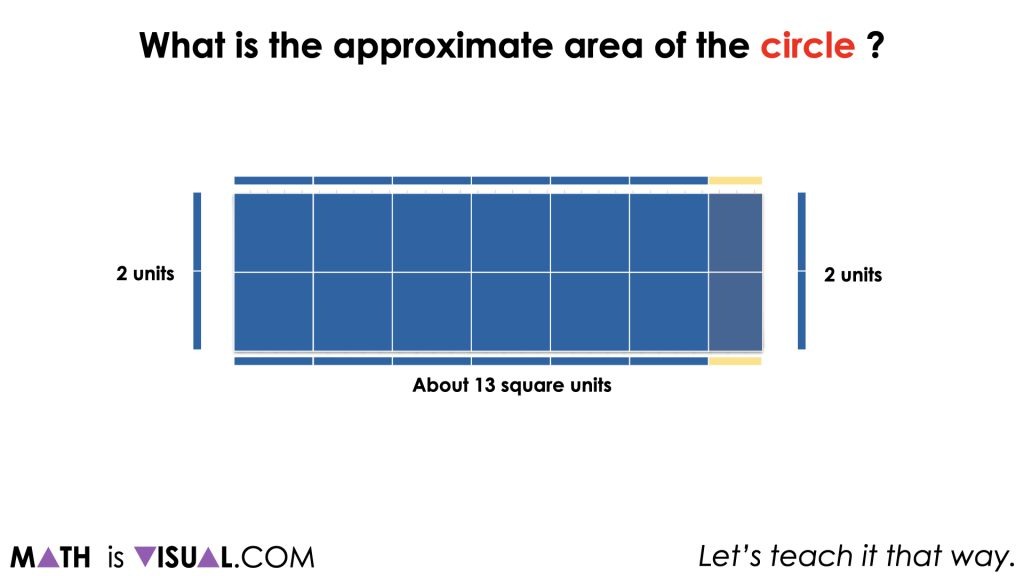
For others, they might still be at a place where they are spatially visualizing how many of the square units will cover the circle (or rectangle). Encouraging students to articulate how they are iterating the square units over the circle (or rectangle) is helpful to ensure that all students are connecting what finding the area truly represents and how it connects to the more abstract representation (i.e.: the formula).
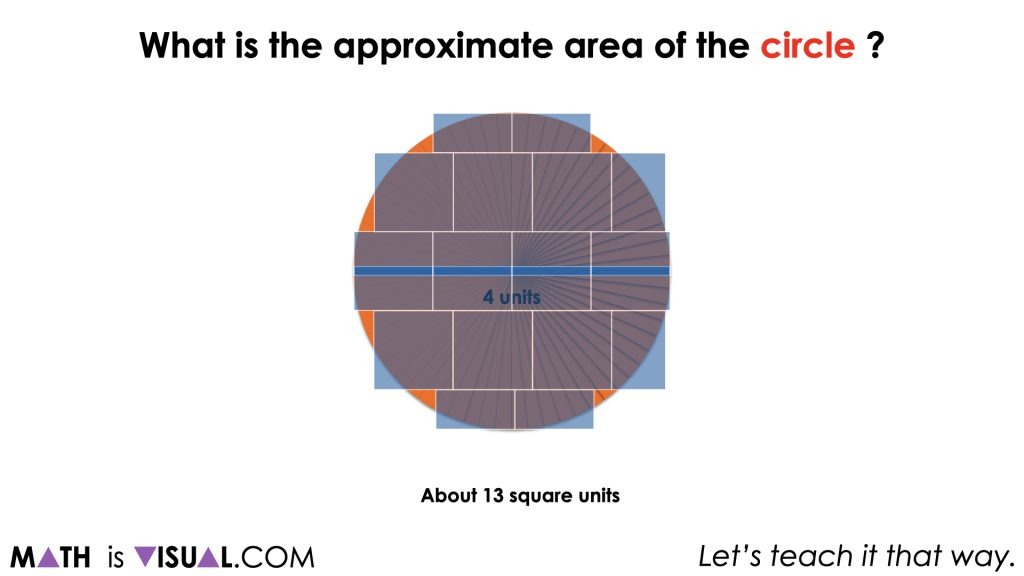
Whether students are spatially iterating the unit square over the circle, over the circle recomposed as a rectangle, or whether they are already using the formula, students should come up with a reasonable approximation of about 12 to 13 square units.
Visual Math Talk Prompt #2
Continue playing the video to move on to the next visual number talk prompt and pause when the prompt appears on the screen for think time:
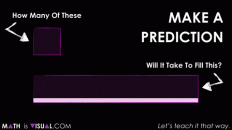
What is the approximate area of a circle with a radius of 4 units?
Make an estimate.
Remind students that the goal for this estimate is to get them visualizing what it means to determine the area of the circle. Some students might visualize square units iterated over the circle, however we want them to start envisioning what the decomposed circle will look like when it is recomposed into a rectangle.
Soon enough, students will begin to realize that the circle recomposed as a rectangle will have dimensions of the radius by half of the circumference. Therefore, before we can approximate with more precision than simply visually iterating square units all over the circle or rectangle, we must determine the circumference of the circle by approximately tripling the length of the diameter.
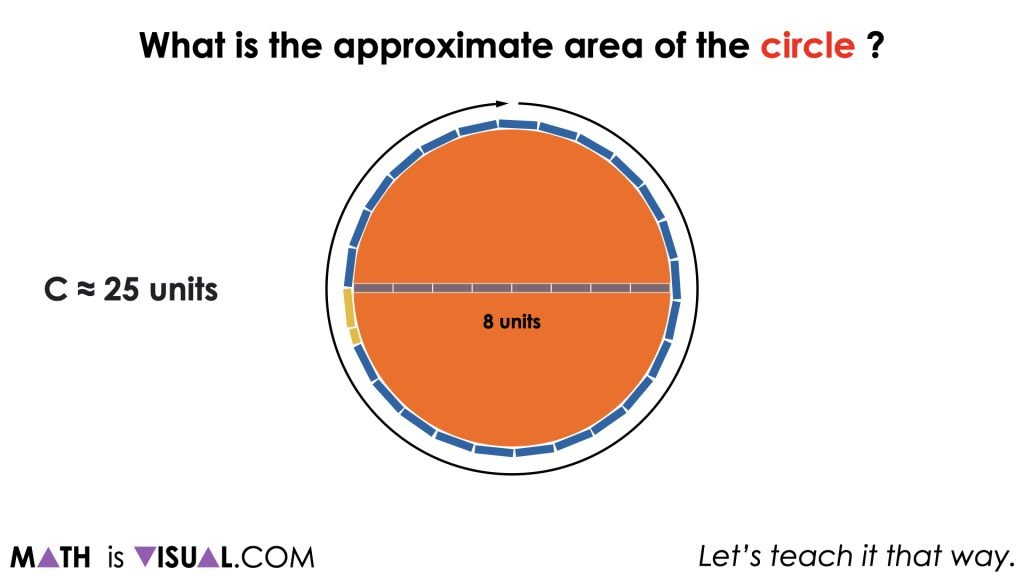
As we decompose the circle and recompose it into a rectangle, we end up with the familiar dimensions of the radius by half the circumference which can be easily used to approximate the area.
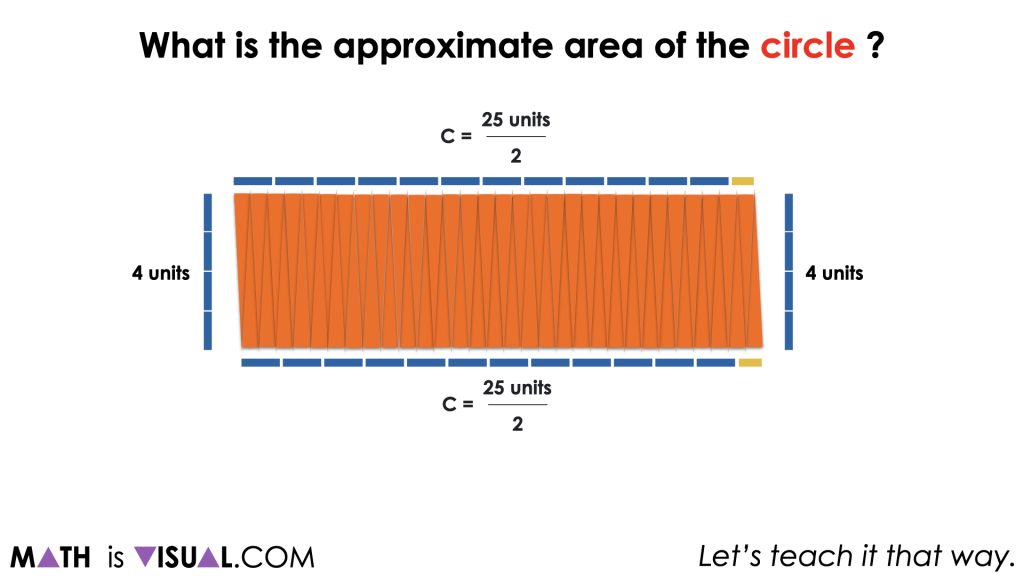
As the facilitator, we want to begin asking students to notice how the radius lives within the length of half the circumference. In particular, you might ask students to approximate how many radius lengths are in the length of half the circumference. They should notice that there are a little more than 3 radius lengths. From here, some students might realize that this is equivalent to π. If they do not, be sure to highlight this so students can begin to make a connection to the actual formula we are using to find the area of a circle, π.
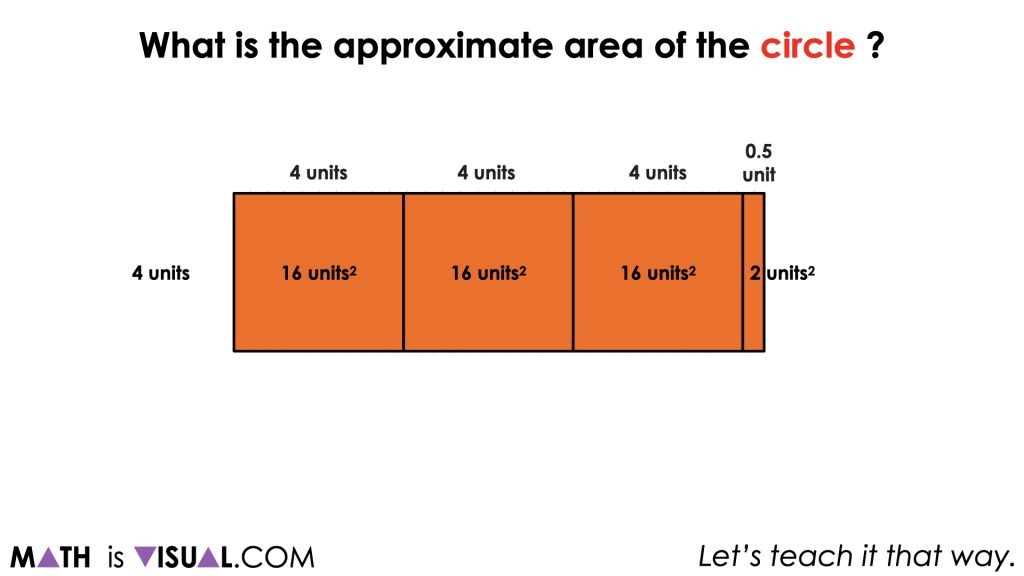
This will hopefully help all students begin to conceptually understand a formula for area of a circle – whether they were already using the formula to find area or whether they were still decomposing the circle into a rectangle.
Want to Explore These Concepts & Skills Further?
Three (3) additional number talk prompts are available in Day 6 of the Going In Circles problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 8-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.
Add comment