Integer Subtraction Using Number Lines and Symbolic Notation

Until the previous post on integer addition, we have primarily used colour to differentiate between positive and negative values. In the last video of the adding and subtracting integers series, we continue using the symbolic notation used to represent negative integers.

The video shown at the top of the post has the entire visual progression of integer addition using symbolic notation.

See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.

Visual Prompts: Question 1, Act 1

Watch the first 40 seconds of the video above before pausing and prompting your students or children to share their thinking for the following:

The goal is for students to begin making the connection between the black squares representing positive quantities and the red squares representing negative quantities. It should be noted that students can pick whatever colour they would like to represent positive and negative as long as they define them.

Since students should have already used the previous integer videos in this series, we hope that children can now see that the symbolic expression -7 – (-4) is the same as “7 red squares take away 4 red squares”.

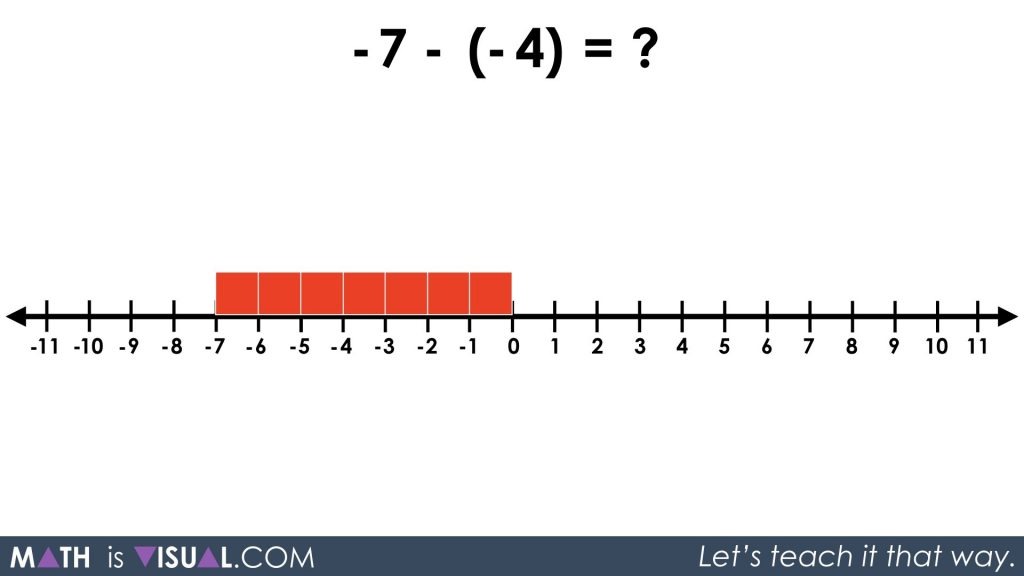
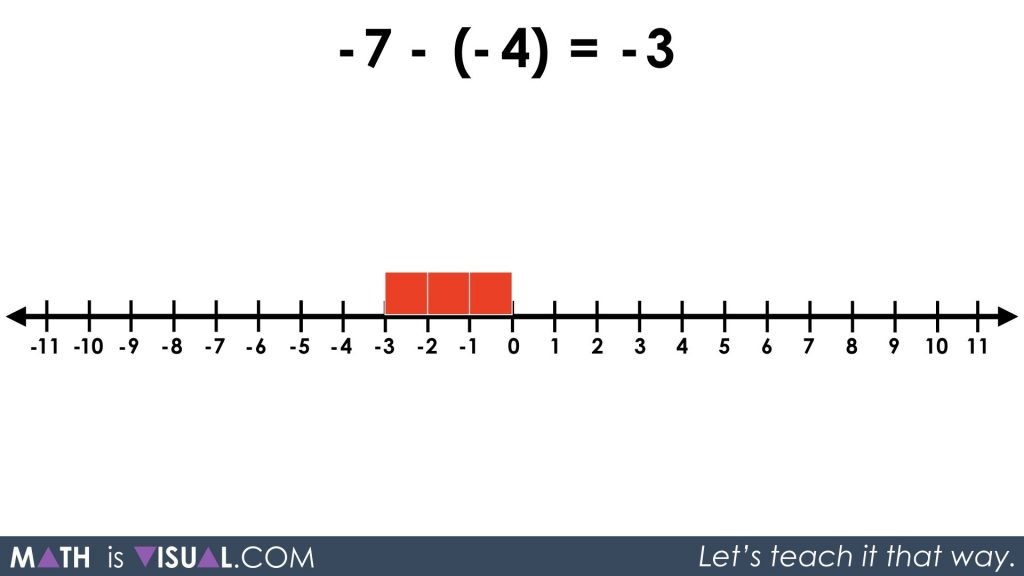
By laying the 7 red squares on the number line, students can visually subtract 4 red squares and see that there are 3 red squares or -3 remaining.

Then, students are asked to determine the result of 5 – (-4).

Since students have had the experience in previous posts to know that 5 – (-4) really means “5 black squares take away 4 red squares” and there are no red squares to remove, we must apply the zero principle to add 4 red squares and 4 black squares.

Now students can take away the -4 or the 4 red squares to leave us with a total of 9 black squares:

We can either count them up by using one-to-one correspondence or we can organize them on the number line to quickly see that the result is 9.

The last visual prompt in the video asks students to compute -6 – 1. We can interpret this expression as 6 negative (red) squares subtract 1 positive (black) square.

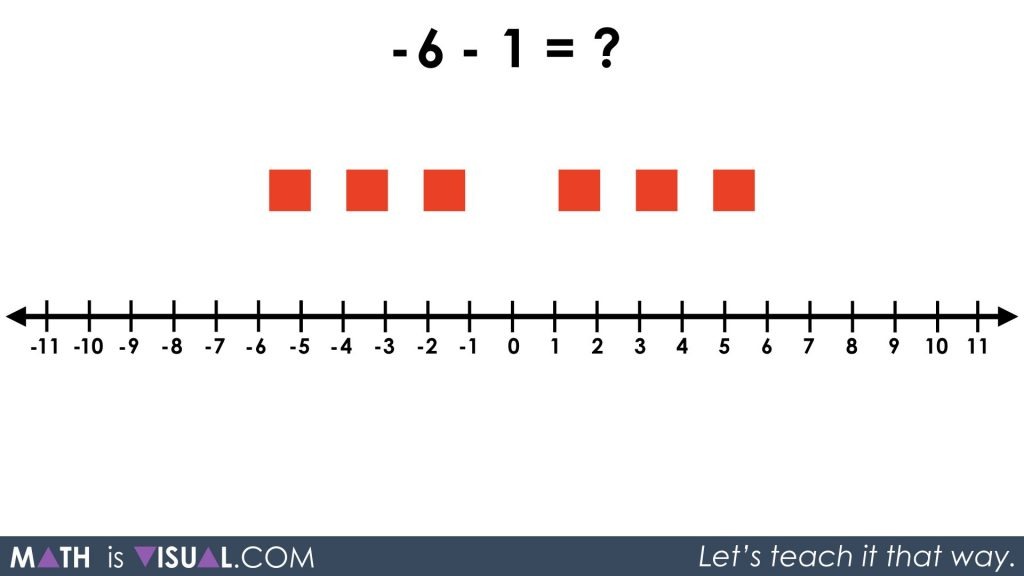
In the last question, we didn’t have any negative squares (red squares) to take away. This time, we don’t have any positive squares (or black squares) to take away. Again, we must apply the zero principle by adding a zero pair. Since 1 + (-1) = 0, or in other words putting a black square and a red square makes them disappear, we have not changed the expression by doing this.

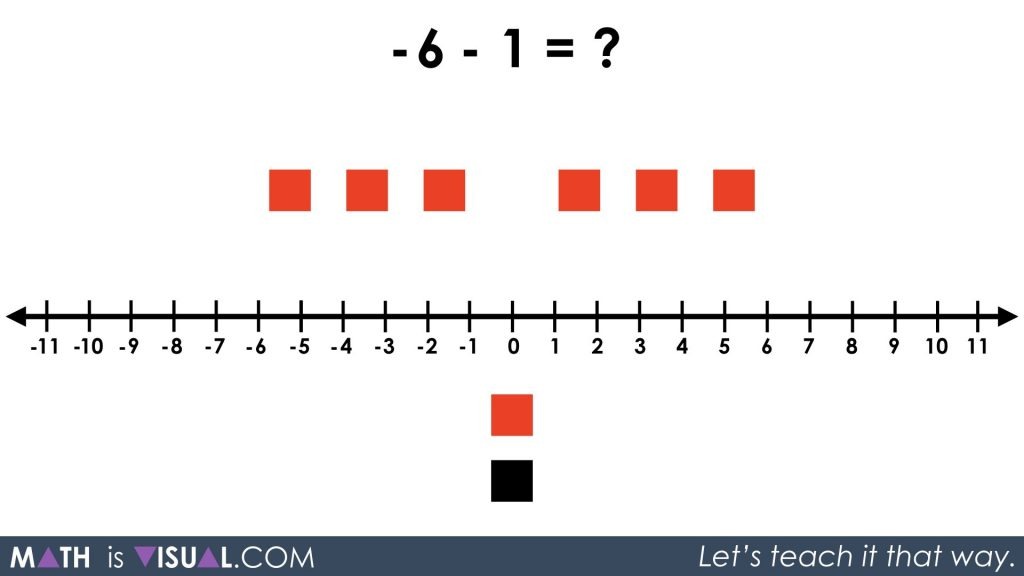
We can now go ahead and subtract the positive (black) square and we are left with -7 or 7 red squares.

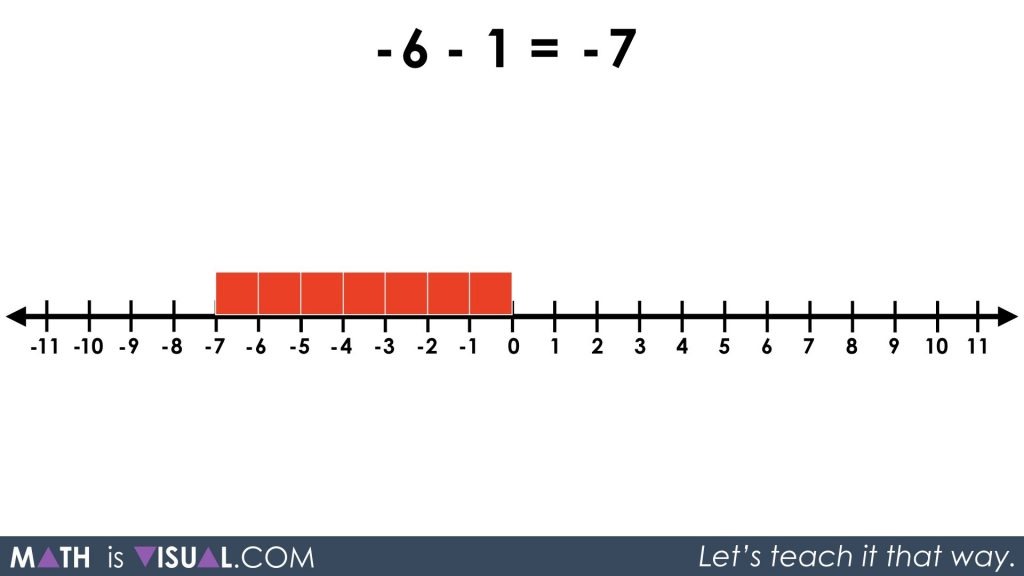
Something interesting about expressions involving integers is how we can interpret them. By looking at the spacing in the question above, it would appear that we have -6 subtract 1 (or -6 subtract +1). However, we could also arrive at the same result by thinking of that same expression as -6 + (-1) because positive and negative values are intrinsically related just as adding and subtracting are opposite operations.

Let’s take a closer look:

By simply adding -1 instead of subtracting +1, we avoid having to use the zero principle. The inverse relationship of positive and negative values has got us covered!

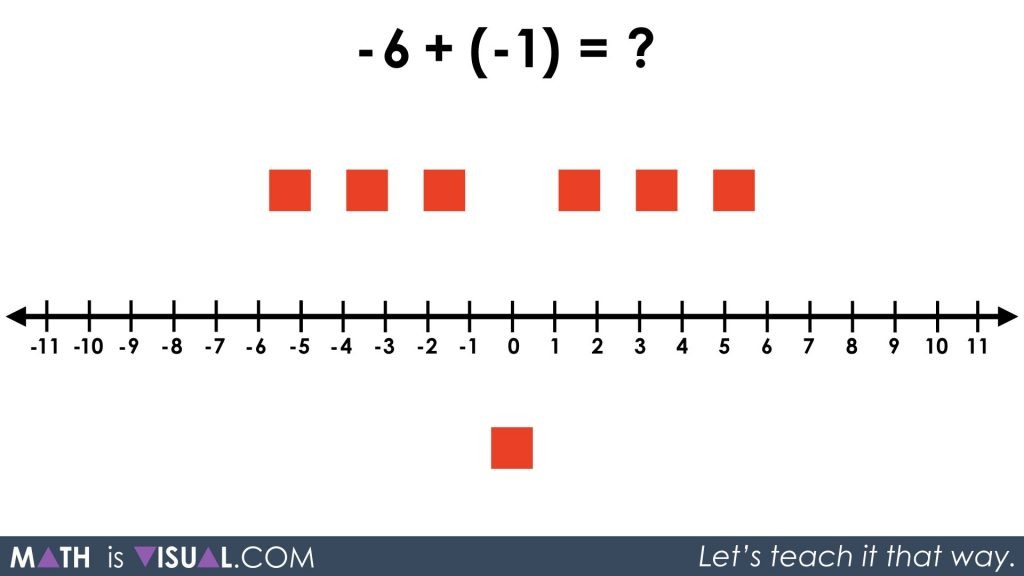
We still end up at the same result:

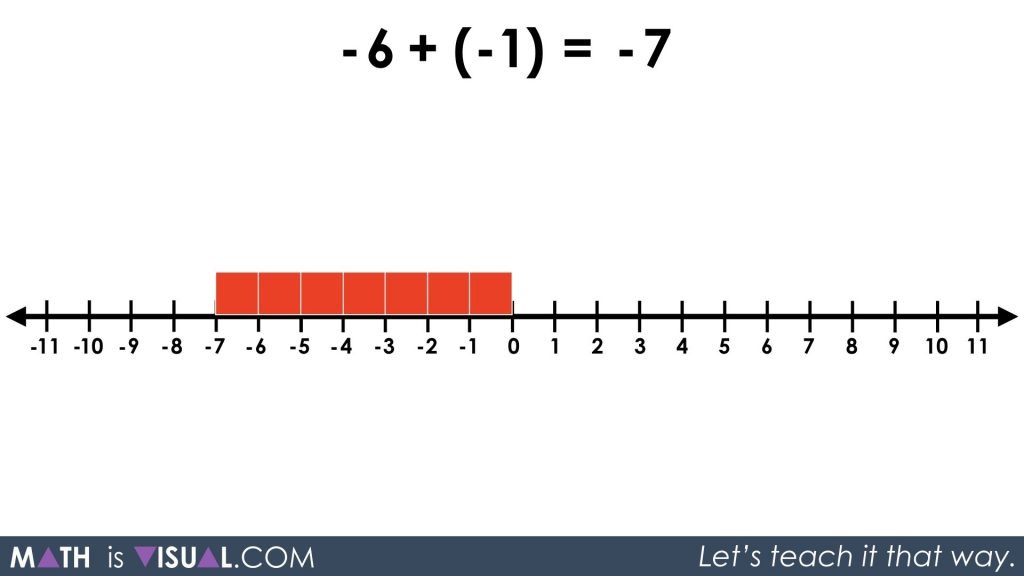
Pretty neat, eh?

Let me know in the comments how you used this activity!