Visualizing the Mean (Average) of a Dataset

In this Math Is Visual Prompt, students are given the opportunity to wrestle with the idea of the mean or average of a dataset visually.

I was taught that you find the mean or average of a dataset by adding up all of the values and dividing by the number of values. While that procedure will always work, I never understood the conceptual underpinnings of what I was actually doing.

Let’s visualize the mean of a dataset by using square tiles to “redistribute” the extra tiles in the larger groups to the groups with less tiles. We then find the mean or average.

Here we go!

Spark Curiosity: What Do You Notice? What Do You Wonder?

As I do in most every 3 act math task, I use the Annie Fetter “What do you notice? What do you wonder?” to spark curiosity while watching the first portion of this video.

Here’s an image of what students/children will be looking at when you are instructed to pause the video:

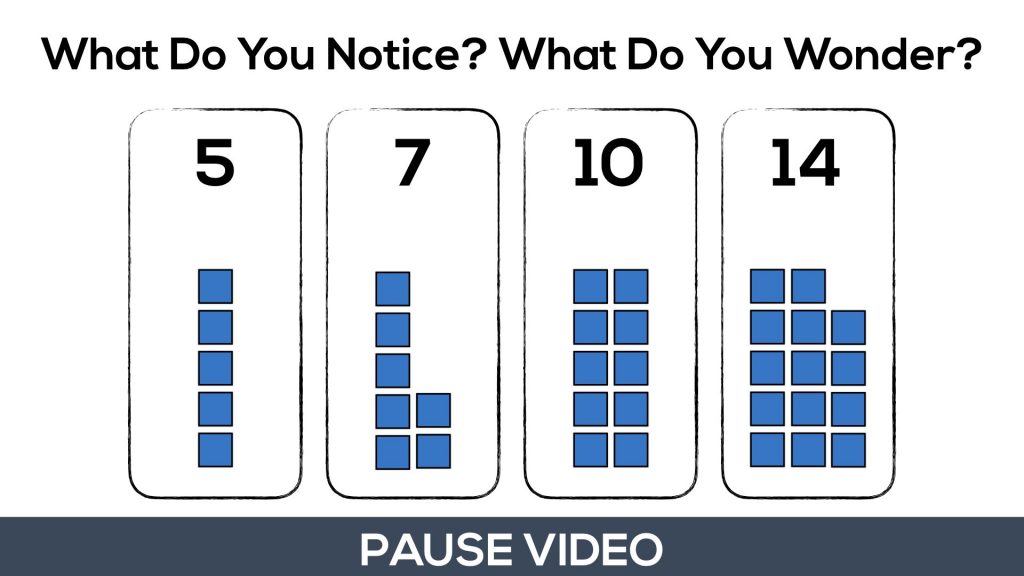
After students share what they notice and wonder, you can then show them the next portion of the video until you’re instructed to pause.

Here, students are asked to determine how many squares should each group have if they were shared fairly?

While students will not know what this idea is called yet, what they are being asked to find is the average or the mean of the dataset.

They will redistribute the tiles to find that each group will end up with 9 squares.

Therefore, the mean or average of the dataset is 9 square tiles.

How’d It Go?

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.

Dive into conceptual 3 act math tasks that engage students and also develop procedural fluency throughout.