Mean, Median and Mode

In This Set of Math Visual Prompts…

Students will determine a single value to represent a data set.  

Intentionality…

This set of visual math talk prompts is taken from the Math Talk section of Day 2 in the Make Math Moments Problem Based Unit called Olympics. The purpose of the Math Talk is to reinforce key concepts and big ideas from this problem based math unit including: 

• There are different types of data;
• Data is often characterized as continuous or discrete;
• Discrete data is often countable and can only take on certain values;
• A measure of central tendency for a data set summarizes all of its values with a single number;
• Mode is the number that appears most often in a data set;
• Mean is the great equalizer; it can be determined by redistributing the data evenly or through partitive division. 

Want to take a deeper dive into these concepts? Consider starting from the beginning of this 5-day problem based unit.

Preparing to Facilitate

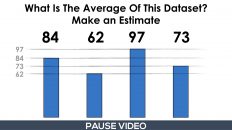
Present the following data set. Ask students to identify a single number to summarize all the values. Name the measure of central tendency used each time and ask students to justify their answer. 

12, 13, 18, 15, 17

Two (2) additional visual math prompts are shared in the Teacher Guide from Day 2 of the Olympics problem based math unit. 

The following Visual Math Talk Prompt intends to Spark Curiosity and lower the floor so all students can enter into each problem.

Visual Math Talk Prompt #1

Begin playing the video to share the first visual math talk prompt and be ready to pause the video to allow for think time.

In the video, students will see the number of points that a basketball player scored for the past 5 games this season:

12, 13, 18, 15, 17

Students are then prompted to:

Determine the mean, median and mode for this data set. 

Which measure of central tendency do you think best represents the number of points scored by this player over the last 5 games?

After pausing the Visual Math Talk Prompt video to give students an opportunity to think and work through this problem, students can then share their thinking including their models and strategies used to determine the mean, median and mode. 

While students who have experience calculating the mean by simply adding the values together and dividing by the number of values in the data set, others might choose to create a bar graph and “redistribute” the extra points scored in game 3 and 5 to games 1 and 2 to average out the number of points. 

This approach is worth highlighting because it truly demonstrates the big idea of the mean as the “great equalizer”.

For the median, rearranging the bars from least to greatest can allow us to easily find the median (or middle) value in the data set.

Finally, with the data set organized from least to greatest, we can easily identify the mode: the value occurring most often. In this case, since the number of points scored in each game was unique, there is no mode.

Want to Explore These Concepts & Skills Further?

Two (2) additional math talk prompts are available in Day 2 of the Olympics problem based math unit that you can dive into now. 

Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.