In This Set of Visual Number Talk Prompts…
Students will build their fluency and flexibility with the magnitude of number by plotting values on a number line, then extend this learning to measures of central tendency by determining the range, mean, median and mode.
Intentionality…
Students will engage in a string of related problems through a math talk to build on concepts introduced during Day 1 of the Piggy Bank unit. This set of visual number talk prompts should be completed without the use of a calculator. This math talk serves to develop a deeper understanding of the following big ideas:
- Fractions can be represented in a variety of ways;
- Fractions (and their decimal representation) represent values relative to a whole (for example, one whole dollar).
- Quantities represented as a decimal are fractions limited to base ten denominators (i.e.: tenths, hundredths, thousandths, etc.)
- Standard representation of coin values are expressed as decimal hundredths.
- Quantities can be represented using a variety of symbolic notations and maintain equivalence.
Preparing to Facilitate This Number Talk
The following visual math talk is a string of related problems that are crafted in a way to foster discussion and the construction of viable arguments. As such, they are open ended and have more than one possible response.
As the facilitator of the following visual math talk prompts, be prepared to notice and name the thinking students are using (i.e.: additive thinking or multiplicative thinking).
While you could simply share the first image with the prompt for students, introducing via the silent solution animations provided may be more helpful. Although each visual math talk prompt video models a possible strategy, we encourage you to represent student thinking by drawing on the board or on the screen rather than simply playing the video and ignoring the thinking of your students.
Visual Number Talk Prompt
Students will first be prompted to think about:
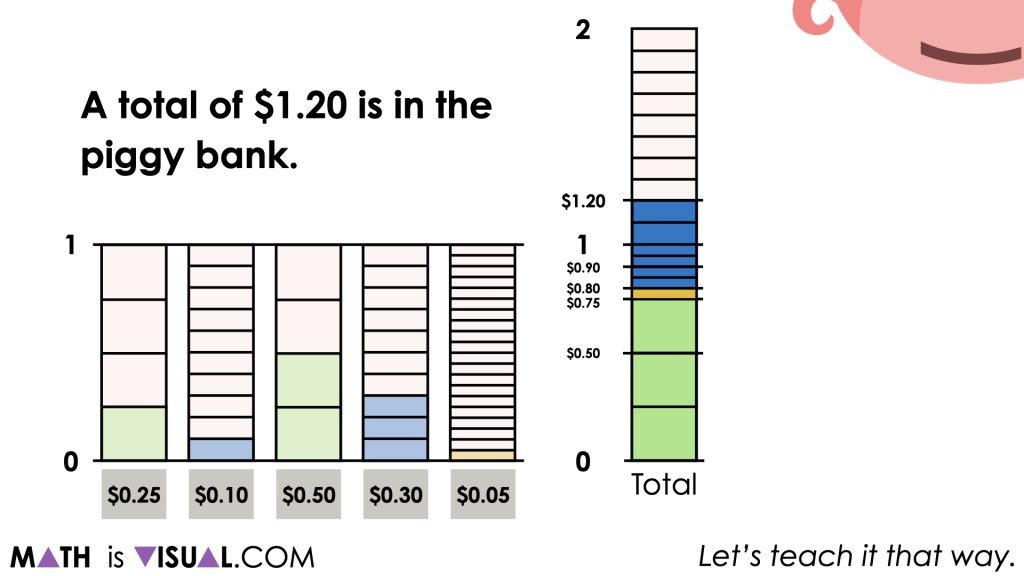
How much money was in the piggy?
How could you convince your neighbour?

Encourage students to turn to their elbow partners or group members and have an open discussion about how much was in the Piggy Bank and how they could convince someone.
While they may (or may not) require a model to justify, we will explicitly highlight with a tape diagram (or bar model) that representing decimal values are derived from fractional amounts. While money is often written to the nearest hundredth (or 2 decimal places), we can “think” of these decimal amounts with more friendly denominators (or sizes of each piece).
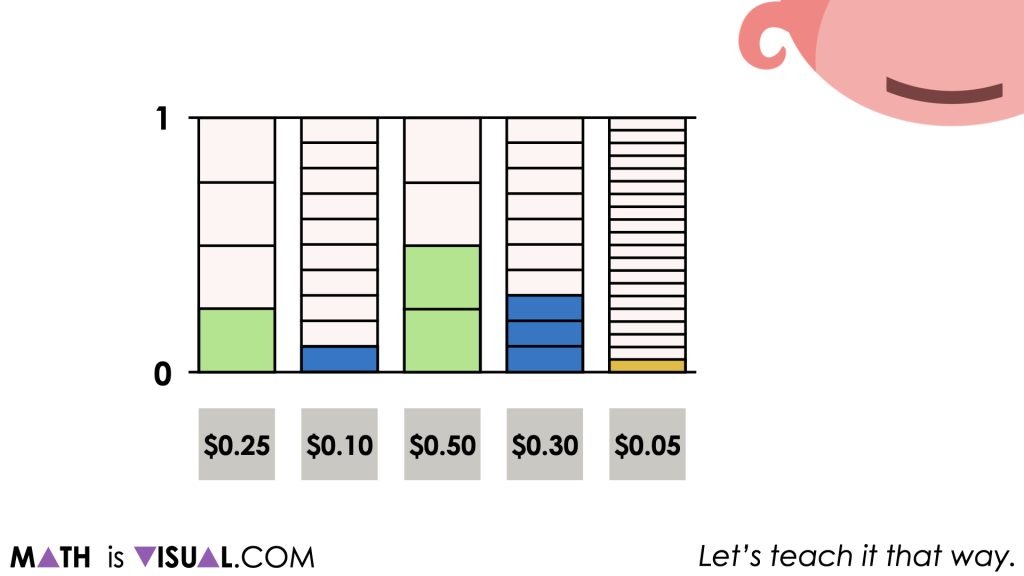
While some students may already have some automaticity for counting change (i.e.: knowing that 1 x $0.25 piece and 2 x $0.25 pieces is equivalent to 3 x $0.25 pieces or $0.75, we can help them make the connection that what they have done is added “3 fourths” or “3 quarters” as a means to highlight fraction and decimal equivalence.
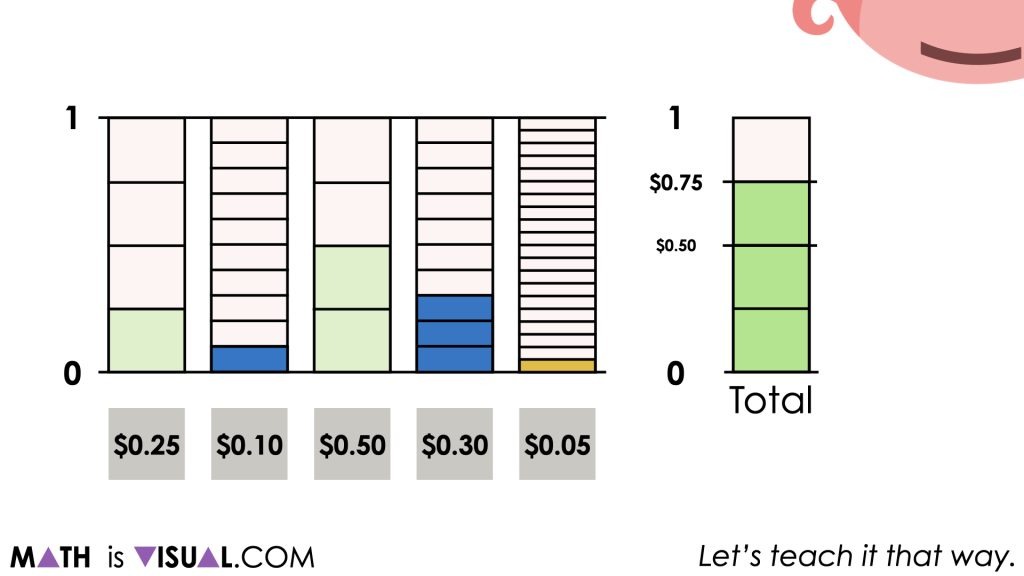
Although some students may have already found the total amount of money from the Piggy Bank, consider asking students which coins they might add to the total next?
Students may have done this in their head or by using their known facts (i.e.: knowing that $0.75 + $0.10 = $0.85), it is helpful to model their thinking either by sharing the visuals from the video or actually facilitating their approach using a tape diagram or bar model.
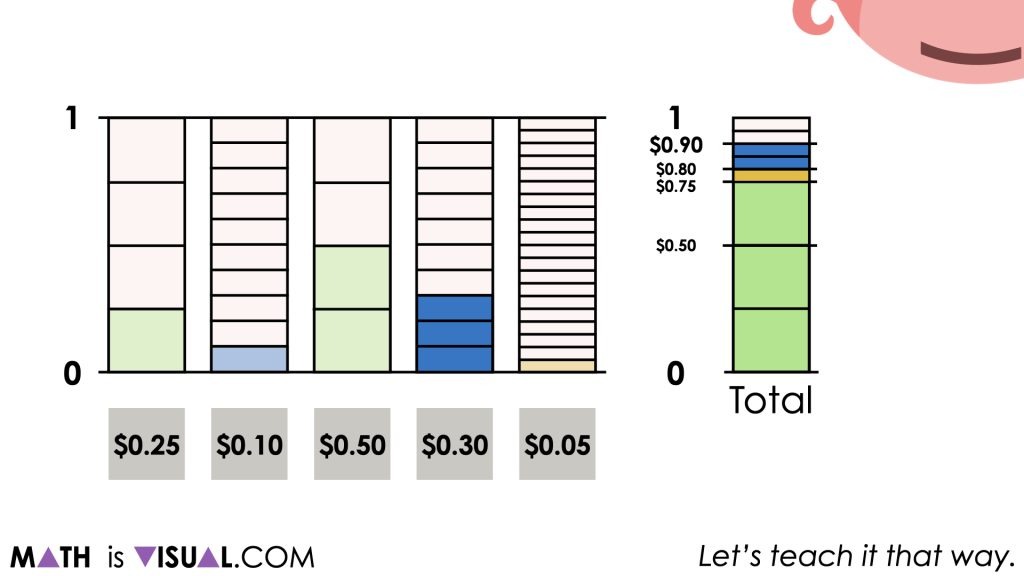
Regardless of how students go about finding the total amount of money from the Piggy Bank, our goal here is to highlight fraction and decimal equivalence as well as introducing them to a mathematical model that has linear and area characteristics that might be helpful for more difficult sums of money (or other fraction and decimal addition situations).
Want to Explore These Concepts & Skills Further?
Three (3) additional number talk prompts are available in Day 2 of the Piggy Bank problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.

![Planting Flowers [Day 2] - Revealing a Rate Through Partitive Division MIV Featured GIF](https://mathisvisual.com/wp-content/uploads/2021/07/Planting-Flowers-Day-2-MIV-Featured-GIF-232x130.gif)
Add comment