Visual Patterns

In This Set of Visual Number Talk Prompts…

Students will extend growing linear visual patterns, make near and far predictions and describe the pattern in words. 

Intentionality…

Students will engage in a visual math talk using visual patterns as a means develop a deeper understanding of the following big ideas: 

• Patterns can be extended because they are repetitive by nature.
• Pattern rules are generalizations about a pattern, and they can be described in words.
• One common use of linear patterns is predicting future events.
• A pattern can be extended to make a prediction. 
• For far predictions, calculations are required for efficiency. 
• In a growing pattern, the values increase.
• In a linear pattern, the values increase at the same rate.
• The rate can be determined by finding the difference between the value of two terms. 
• Graphical representations of linear growing patterns appear as straight lines.
• The initial value in a linear pattern is the constant.
• When the initial value is not zero, the relationship between the two variables is not proportional.

String of Related Problems

Present the following visual pattern one at a time.  Ask students to describe the pattern rule in words, including the initial value. In order to determine the initial value, students are encouraged to determine the value of term 0.

Ask students to predict the value of the 8th term and the 14th term. Students are encouraged to justify their thinking. Look for opportunities to build efficiency. For example, once students have determined the rate, and the initial value, rather than counting on or repeated addition, can students leverage this information to perform a calculation? 

For example: In the first pattern, the rate is 3, and the initial value is 1. Students can multiply the term number by 3, and add 1. Term 5 multiplied by 3 is 15, plus 1 is 16.

Visual Number Talk Prompt

Students prompt:

Use manipulatives or draw what you think might come next.

After giving students enough time to create (using square tiles, unifix cubes, etc.) or draw what might come next for Day 3, ask them to share their thinking with their neighbour before sharing out to the class. 

Before resuming the video to reveal what the figure for Day 3 looks like, be sure to celebrate the different possibilities shared encouraging them to explain their thinking. It is important to also explicitly explain that while all of the figures shared are all possible, we are going to explore a specific pattern that has a Day 3 figure that looks like this.

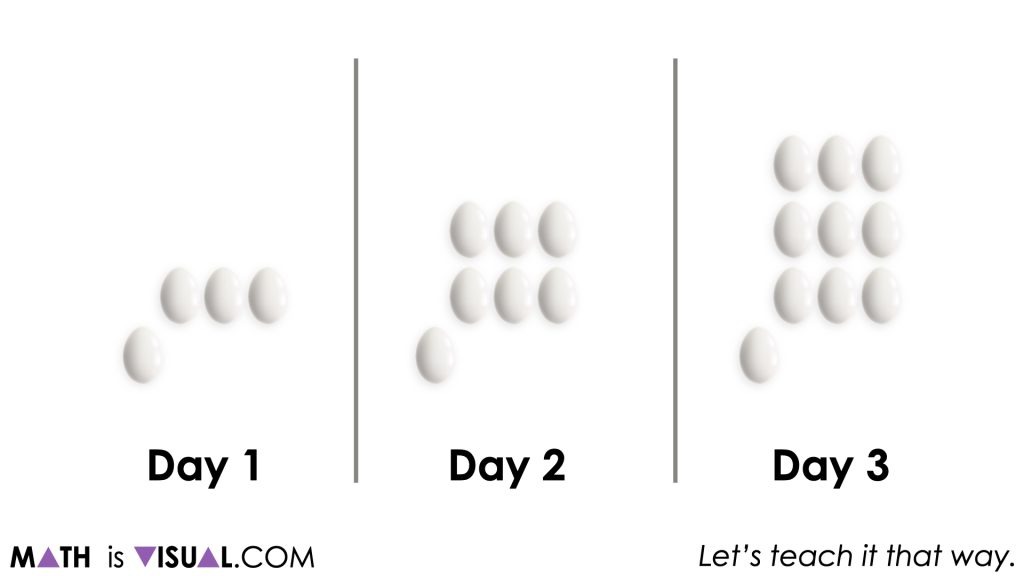
If any students in the room had successfully anticipated the figure for Day 3, be sure to celebrate and ask students to recall the thinking that those students had shared previously to help them predict what they think might come next for Day 4. 

Student Prompt:

What might come next for Day 4?

Create a figure using manipulatives or by drawing.

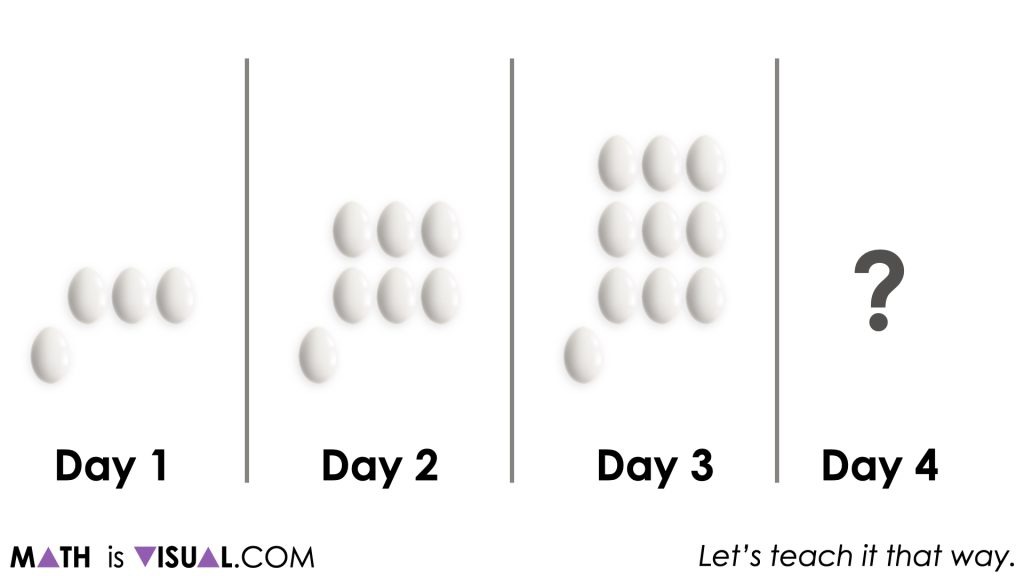
Similarly, give students an opportunity to share their thinking with each other. Pay close attention to which students are already noticing a linear growing visual pattern forming and encourage them to continue to verbalize how they see the pattern growing prior to revealing the next figure.

Although you may have already encouraged some students to verbalize how they see the visual pattern growing, be sure to explicitly have all students now:

Describe the pattern rule in words.

It can be helpful to frame this request using a script such as the following:

Pretend that you are on the phone with another student who isn’t present today and cannot see the pattern we are all viewing right now. How would you communicate how they should create each of the first four days in the pattern?

At this point, we hope that students are able to articulate the growing visual pattern as something similar to:

Begin with 1 and increase by 3 each time.

Be prepared for some students to say something like:

Begin with 4 and increase by 3 each time.

However, the true initial value of this linear growing pattern is actually 1 and not 4 since the true “beginning” of this pattern is on Day 0, with 3 less than Day 1.

At this point, we can challenge students to use their visual pattern rule to:

What will Day 8 look like? 

What will Day 14 look like?

Describe how you could construct each figure without simply giving the total number of eggs in each figure.

At this point, the goal is that students are able to articulate this visual pattern growing at a rate of 3 eggs per day after beginning with a single egg. 

Some students might articulate Day 8 as something like:

8 rows of 3 eggs forming a rectangle with a single egg off of the bottom left corner of the rectangle.

Of course, writing out an algebraic expression for this pattern (i.e.: 1 + 3d) or an algebraic equation (i.e.: N = 1 + 3d) can be helpful. 

Want to Explore These Concepts & Skills Further?

Three (3) additional number talk prompts are available in Day 2 of the Bird Migration problem based math unit that you can dive into now. 

Why not start from the beginning of this contextual 8-day unit of real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.