Developing an understanding of magnitude is so important for students to build number sense, yet many students can find this to be a challenge.
One of the biggest problems with magnitude is our inability to relate large quantities to other quantities and visualize them spatially on a number line.
What do I mean by large quantities? Well, that depends on the learner.
For a student in Kindergarten, large quantities might mean numbers greater than 19.
For a student in middle school, that might mean numbers larger than 10,000.
What numbers do you struggle to visually relate and compare to one another? In this Math Is Visual Prompt, we’re going to borrow an idea that Mark Chubb shared on Twitter a while back:
Where does 1 billion go?#mtbos pic.twitter.com/srA8umAFsx
— Mark Chubb (@MarkChubb3) November 29, 2016
In this Math Is Visual Prompt, students are challenged to determine where 1 billion goes on a number line from 0 to 1,000,000,000,000 with some animations building off of what Graham Fletcher had done in one of his talks recently.
It’s harder than it looks!
As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and visually after consolidating in the classroom through student work.
Let’s get started…
Sparking Curiosity
In the first portion of the animation video, you give students some time to think about where 1 billion should go on the number line from zero to 1 trillion:

Then, I suggest following Graham Fletcher’s lead and getting kids to stand up (or maybe use a “thumbs up”) and then they can sit down (or “thumbs down”) to represent the point at which they believe the dot is at the 1 billion mark of the number line.

Have students convince their neighbours.
Do you agree with your neighbour? Why or why not?
The Reveal
Many students (and adults) are surprised when they realize that the dot is almost touching the hashmark where zero is on the far left of the number line!

That is because 1 billion is 1 one-thousandth of 1 trillion!
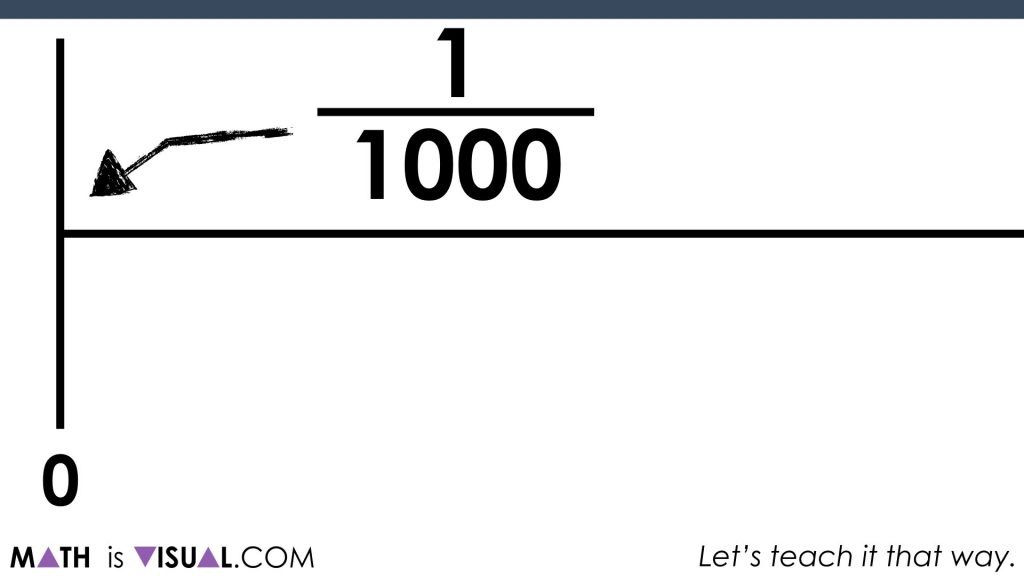
Pretty neat!
The best part of this idea is trying to think about what is the “zero to 1 trillion” number line for YOUR students or children at home?
Is it 0 to 20 for a pre-schooler/kindergartener?
Is it 0 to 10,000 for a middle schooler?
Where about does their understanding of magnitude break down? Let’s work on where they are at and push them a little further each day.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.


I know it’s summer and we are on holidays, but this is when I do all my research/reading lol. This was done in my grade 7 class and I had 1 student divide the line equally into 3 segments and she put 1 billion 2/3 of the way. Her reasoning: she divided the line into 3 sections – one for a million, the 2nd for a billion, and the third being a trillion. She did this quite quickly and was able to justify her answer. Do you think there is a next step for her or do you think she just already ‘gets it’?
Hi Michelle,
If 1 million was half of 1 billion and 1 billion was 2 thirds of 1 trillion, then she’d be rocking. However, the true relationship is that 1 million is 1 thousandth of a billion and 1 billion is 1 thousandth of 1 trillion.
So rather than partitioning the line into thirds, she’d need to partition the line into 1 million parts…
As for next steps, I would ask questions around how she “knows” that her number line is correct and how she could convince you.
Then, if she’s still confident that her number line is accurate, I might ask questions like:
“when I look at your number line, it appears that 1 million is half of 1 billion and 1 million is 1 third of 1 trillion… is that accurate?”
If she’s still confident here, then I might ask:
“it also looks like if this (pointing at the 1 third partition hashmark) is 1 million, then this (pointing at the 2 third partition hashmark) would be 2 million. Are you saying that 2 million is equivalent to 1 billion?”
This type of purposeful questioning is what I have been trying to work on in my own teaching practice to help me be less of an answer / advice giver and more of a curious questioner.
Awesome – thanks for replying