In this series of Math Is Visual Prompts, students are given the opportunity to begin moving from counting sets (i.e.: individual objects like candies, toy cars, bugs, etc.) to the very early stages of linear measurement through the use of “number paths” on their developmental trajectory towards the eventual use of the much more abstract number line.
As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and after consolidating in the classroom through student work.
Let’s get started…
Introducing The Number Path
Note that a number path looks an awful lot like a number line, however you’ll notice that each “square” is labelled explicitly instead of at the “end” of each unit (on each ‘tick’). This is to promote students explicitly counting each square to make the thinking much more accessible for early counters.
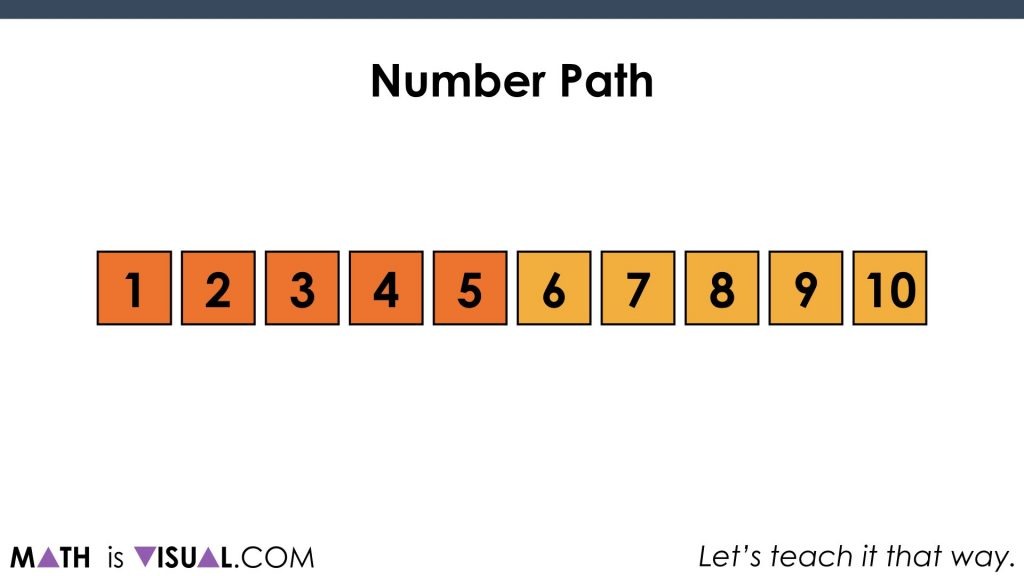
While this is slightly more abstract than counting say actual dinosaurs or donuts, it is much less abstract than looking at a line with ticks on it.
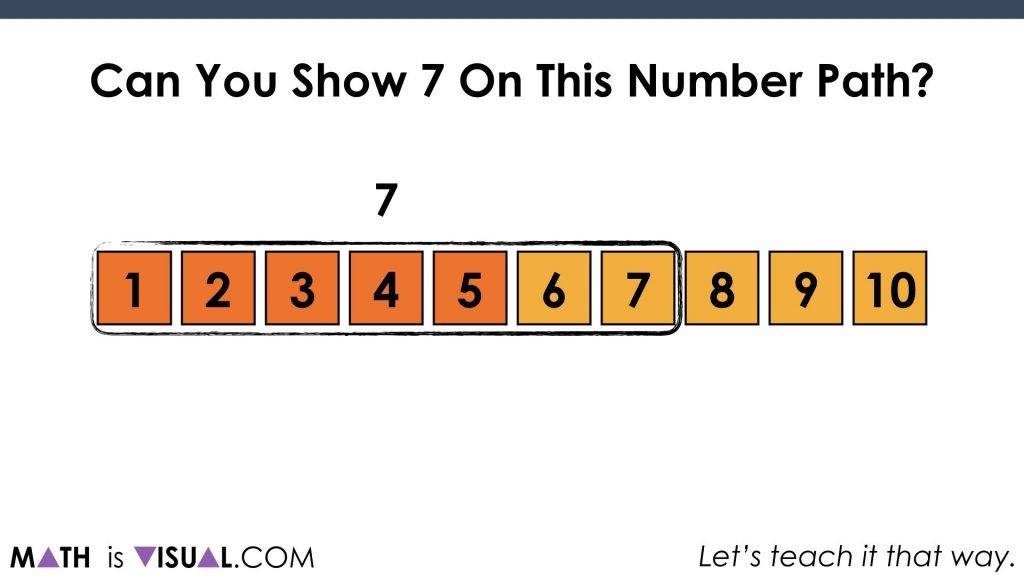
Show Me…
We then ask students to “show 4 on the number path”. What we are looking for is students showing that 4 includes 4 squares and not just the last square. This builds on the idea of cardinality.

We then ask to show 7 with the number path:
Composing Numbers Through Early Addition
Then, we start asking students to show a number and then add some.
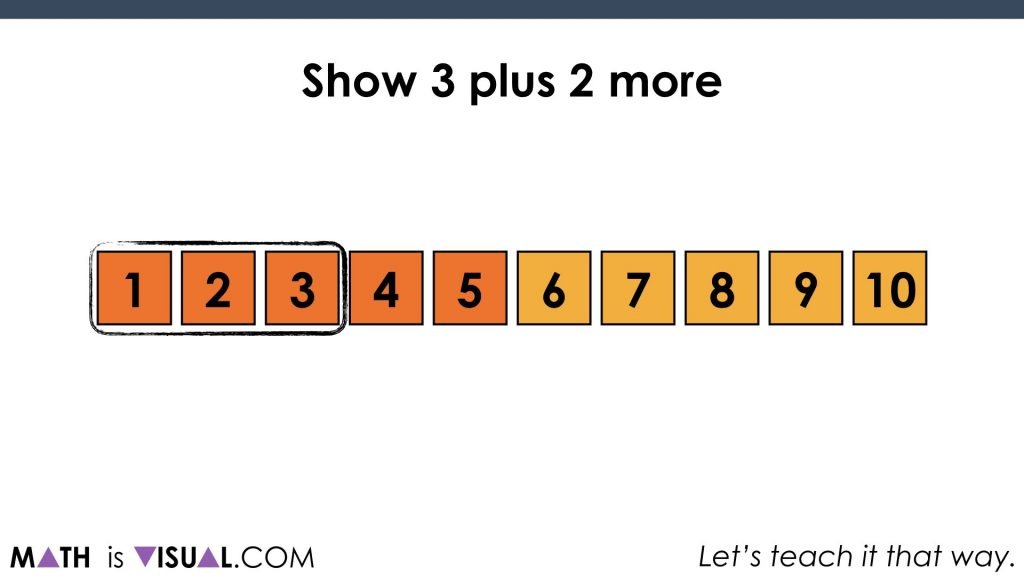
After adding two more, we get these two groups of 3 and 2 on the number path:

Finally, even a student who is still counting all can come up with the newly composed quantity of 5:

Something to note here is also the fact that there is this idea of hierarchical inclusion lingering plus the idea that when you put together a quantity of 3 and another quantity of 2, you get 5. You can also highlight that the quantity of 5 can be decomposed into a group of 3 and 2.
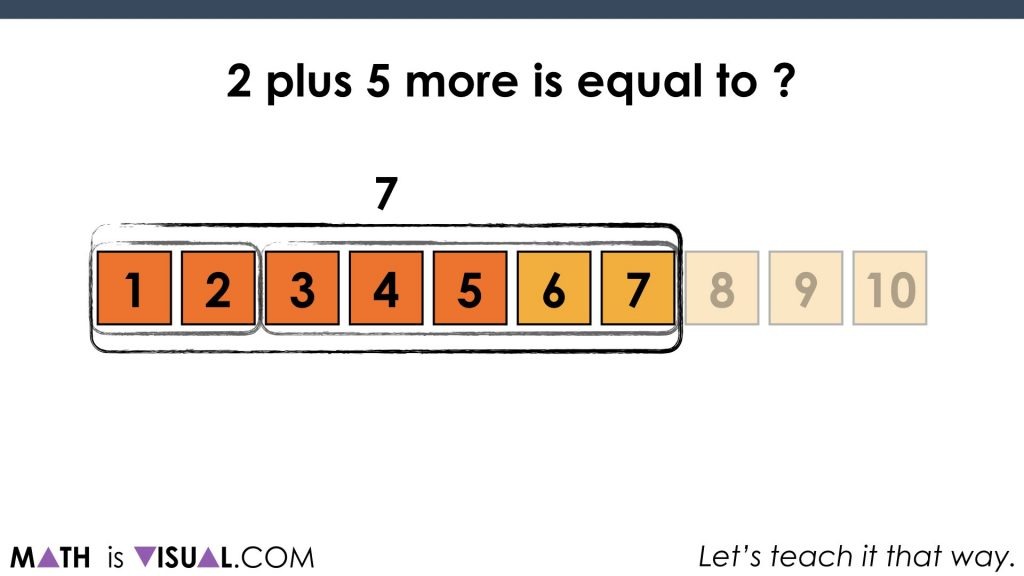
We then do this again for 2 plus 5 more:
Decomposing Numbers Through Early Subtraction
We then do something similar for early subtraction and decomposing numbers such as 8 remove 5:
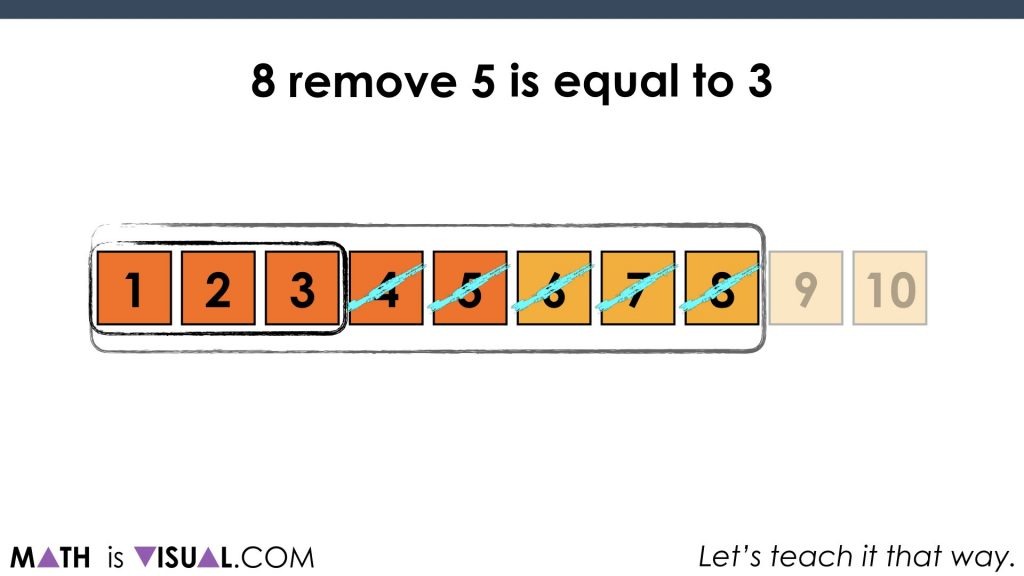
as well as 9 remove 3:
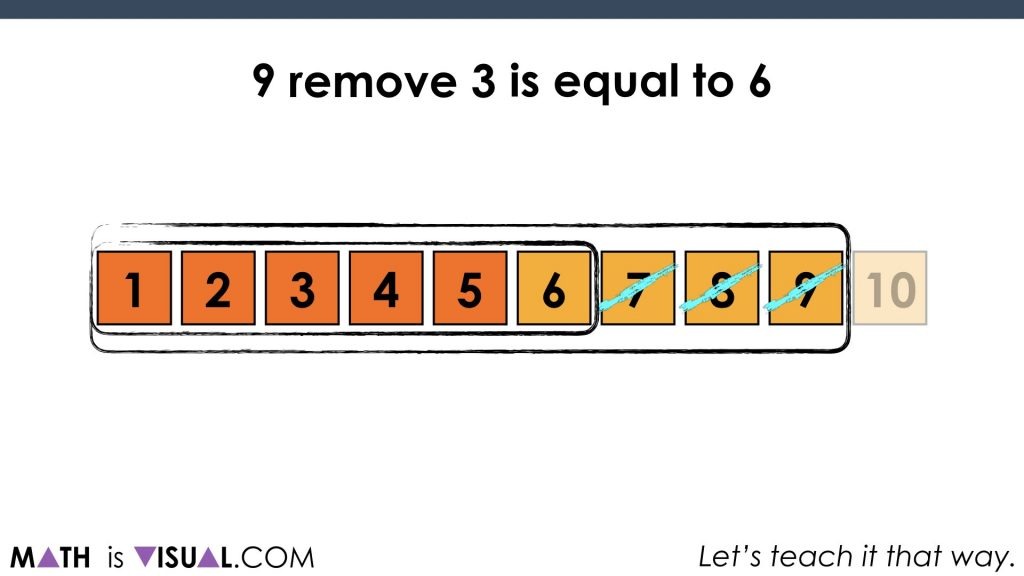
So there you have it. We are well on our way to start thinking mathematically with linear models through the use of a very concrete and countable approach we call the number path.
How’d It Go?
Thanks for watching and reading!
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.
[…] we must introduce the number path. There is another activity here that might be beneficial if students have not experienced a number path as of […]
[…] let’s start with the number path like we did in a recent set of Math Is Visual prompts and connect this idea concretely to a number line by building concrete number […]
Really like the idea of the number PATH compared with the number line. Far more impact for both composing and decomposing. Was interested though to see you remove three from eight, etc from the RIGHT side of the path. My brain was thinking remove the 5 (larger number) to leave the 3 of the 8 group. But fully get the LOGIC to that now, especially after seeing the second example. Great video; great ideas! Thank you so much.