Unitizing and Repeated Subtraction

As you know from the variety of topics and grade bands covered on the Math Is Visual website, visualizing mathematics is really important; first concretely, then pictorially, and finally, symbolically. 

While I stress the importance of mathematical models for thinking and representing mathematics, it is common for educators to promote emerging certain mathematical models before students are developmentally ready. 

In this series of Math Is Visual prompts, we will use concrete number lines, visual (drawn) number lines, and even share how a student might use an array using cubes to solve a challenging standardized test problem involving unitizing and repeated subtraction.

Remember that you can use any set of Math Is Visual prompts as lesson starters, math talks, number talks, or number routines in the classroom or at home with your kids!

As always, do not pre-teach how to solve problems similar to this one. Allow students to investigate by pausing where indicated and to defend their strategies using mathematical models of their choosing.

The silent solution visuals provided after the prompts may be used as a consolidation only AFTER students are given the opportunity to work with these ideas concretely and visually and after consolidating in the classroom through the use of student generated solutions.

Let’s get started…

Sparking Curiosity

Let’s take some time to Spark Curiosity using the Make Math Moments “Curiosity Path” as we always do.

In this case, we will start with a super low-floor prompt asking students to determine “how many?” of the blue cubes on the screen.

The visual prompts give time between each for students to think and describe to a neighbour.

Then, we begin sharing “units” of 10 on the screen and we ask students to once again determine:

How many?

Pause where the visual prompt video indicates and give students some time to convince their neighbours.

The units of 10 are intentionally selected to encourage students to skip count by 10s.

We then stop and ask students:

How many groups of 5 cubes can you make (with 70 cubes)?

Again, be sure to give students an appropriate amount of thinking time and allow them to convince neighbours and the whole group.

We’ll then extend this thinking and ask students to determine:

How many cubes would be left after removing 6 groups of 5 cubes?

Again, pausing the video for students to engage in their own thinking and to construct an approach using a strategy and mathematical model that serves them best. 

After giving students an opportunity to share their own generated solution strategies and models, you might consider connecting some of their thinking to the following approaches.

Here, we show a concrete number line where we make our 6 groups of 5 cubes and then count the remaining cubes. 

… some students might make jumps on a number line or double number line:

And other students might make various jumps using different units of 5, 10, or maybe one big jump by a unit of 30:

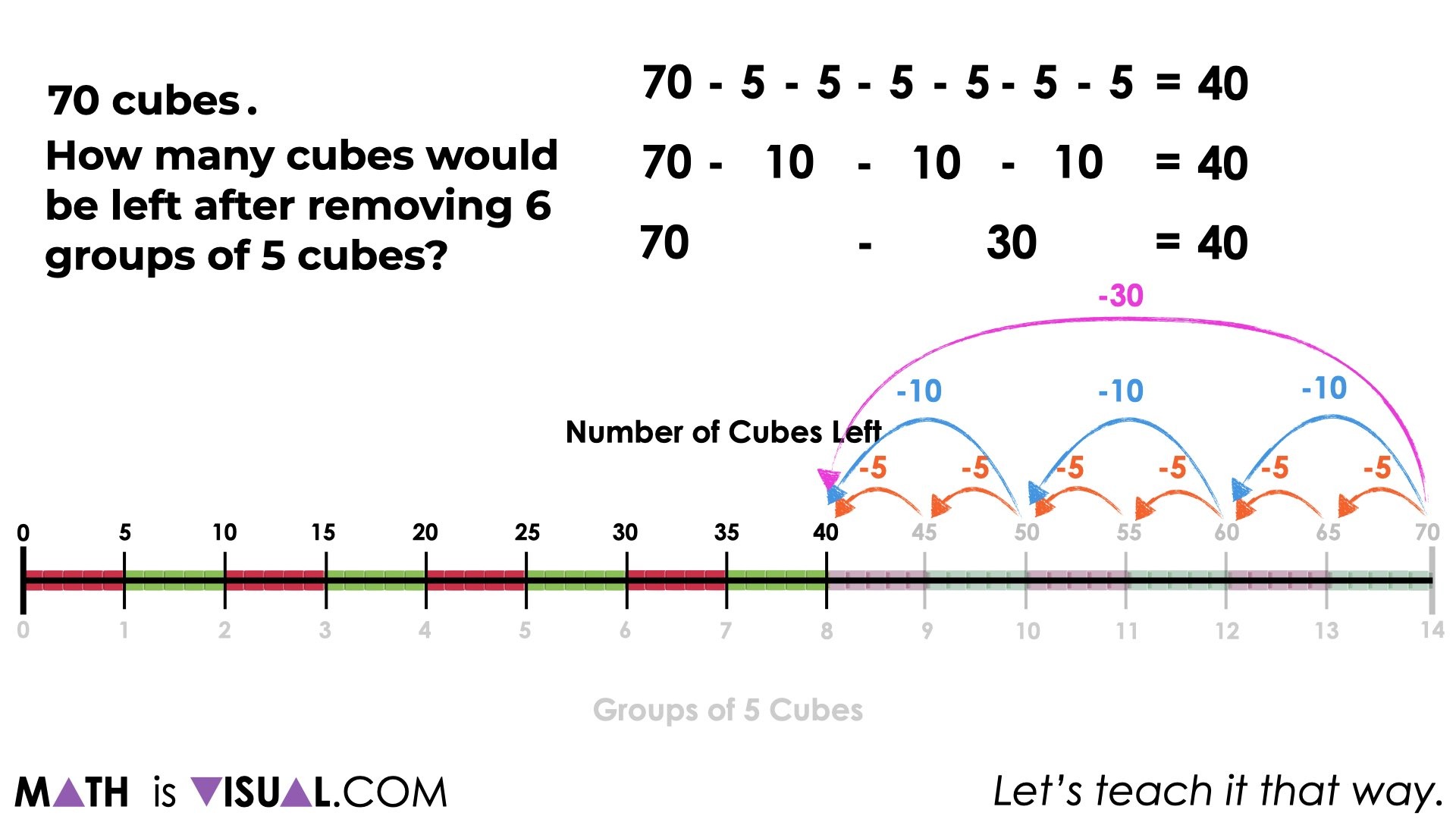
Some students might simply use symbolic notation because they have the known facts to help them. If this is the case, you might want to ask students to describe how they know or how they could convince you to ensure that they aren’t soley relying on memorization without understanding. However, if you are confident the student has the understanding (i.e.: has shown you this understanding before) then this may be unnecessary.

Some students might use an array model: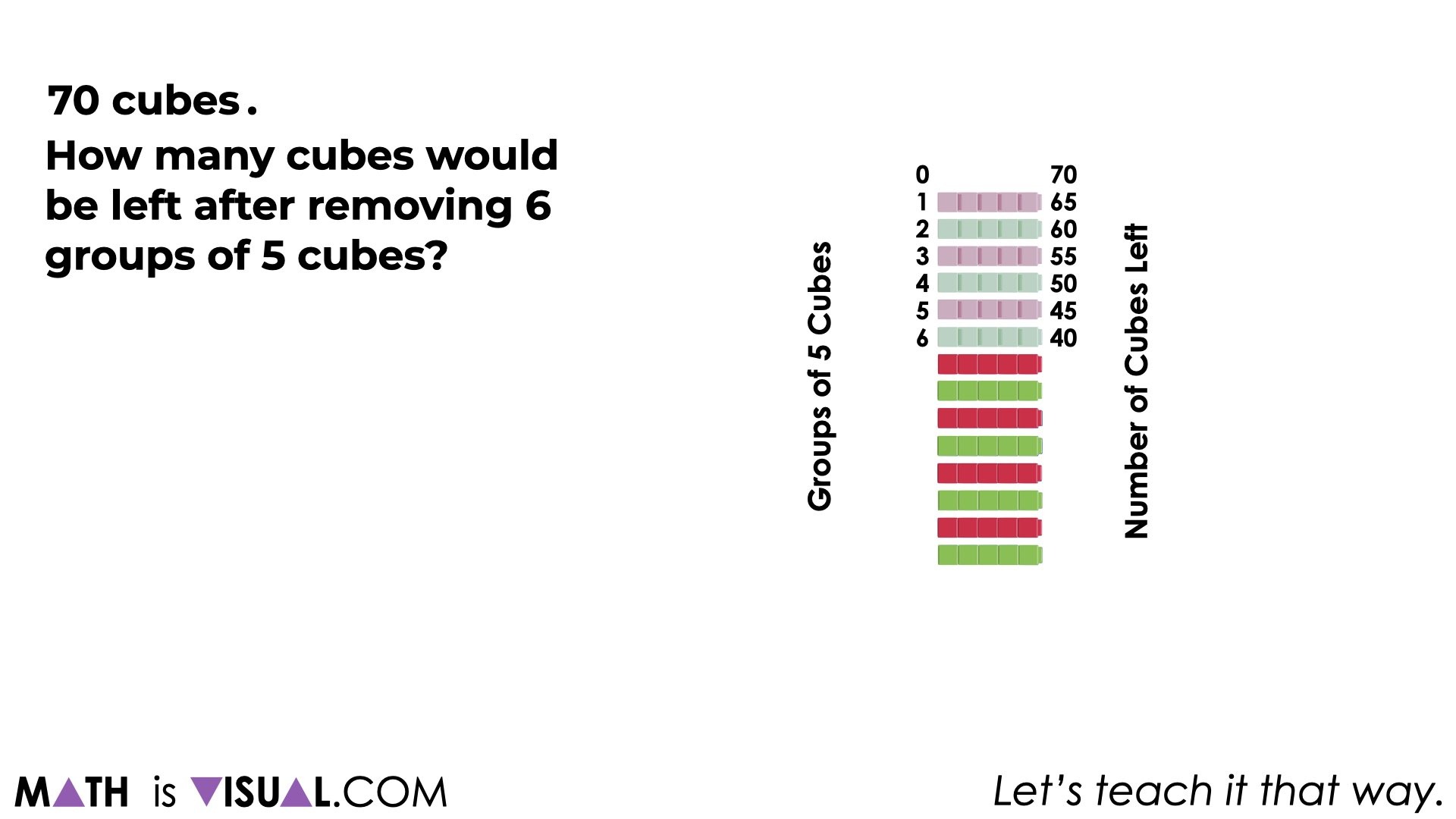

While this task might seem pretty low-floor, I hope you recognize that the final prompt is actually a pretty cognitively demanding task for many students. This task was inspired by an EQAO Assessment of Mathematics question from the Grade 3 Standardized Test in Ontario that most students performed very poorly on.

Here it is:

Lucy has 70 beads.

She uses 5 beads to make each necklace.

How many beads does Lucy has left after she makes 6 necklaces?

While we want to help students build the understanding, skills, and confidence to solve word problems like the one above, we must remember to do so gradually. 

So, start concrete and work your way to visual mathematical models prior to pushing word problems and symbolic notation before they are ready. 

====

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.

Be sure to dive into our problem based math lessons that Spark Curiosity and Fuel Sense Making through the use of visuals.