Understanding Area of a Circle Conceptually

In this series of Math Is Visual Prompts, students are given the opportunity to wrestle with the idea of area – in particular the area of a circle – through a “Would You Rather” situation.

This particular series of Visual Prompts were extended to be used as the 4th day in our Make Math Moments circle measurement problem based unit called Going In Circles! In the 8-day unit, you’ll emerge the idea of Pi, bump-into the formula for circumference of a circle, extend this thinking to area of a circle and engage in math talks and purposeful practice throughout.

As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and after consolidating in the classroom through student work.

Let’s get started…

Spark Curiosity: Would You Rather…

Ask students “Would You Rather two 12 inch medium pizzas or one 18 inch large pizza?” to spark curiosity and pause where indicated in this video.

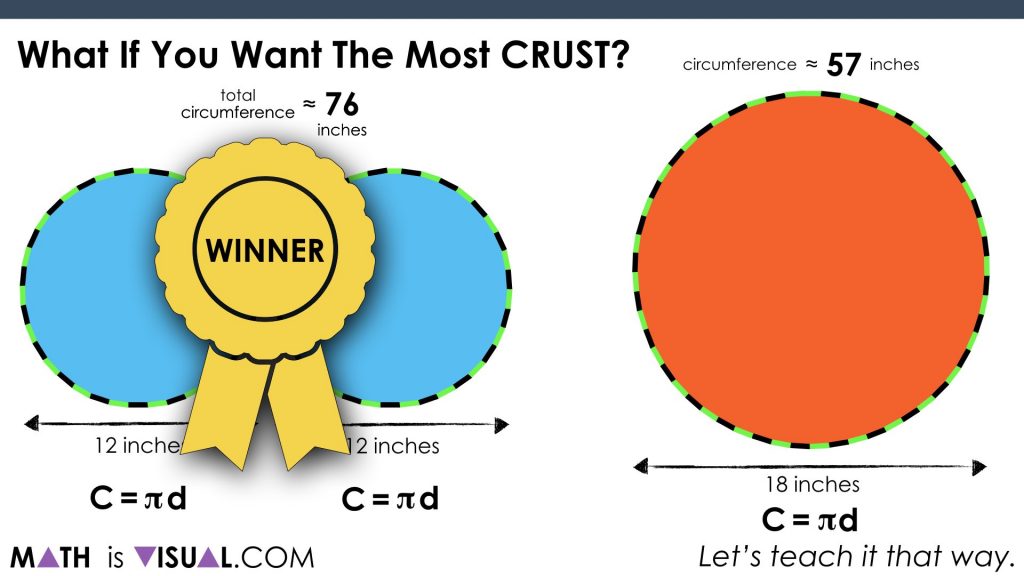
What If You Want The Most Crust?

After they all share out, challenge them to think about whether they want to change their answer if you were looking for the situation with the most crust:

At this point, we want them to start digging in. Be sure to ask them to convince their neighbours as we want to move beyond just gut shot guesses.

This is a great opportunity for students to “play” with the idea of circumference as it relates to the diameter of a circle. As they may (or may not) be aware, the ratio of the circumference to the diameter is approximately 3.14:1.

Yes, it is π:1!

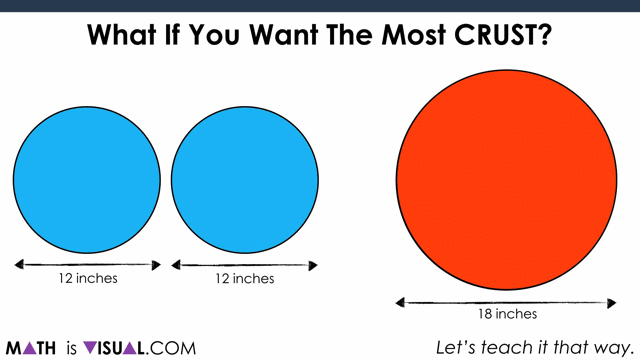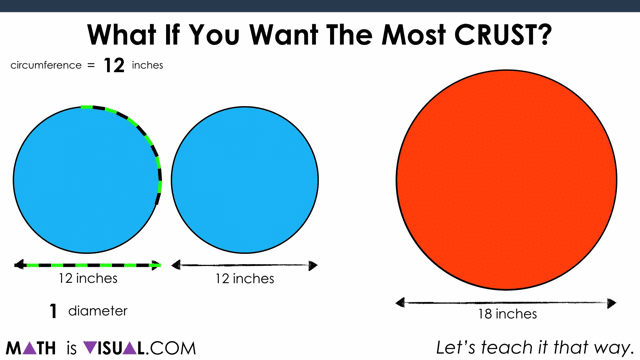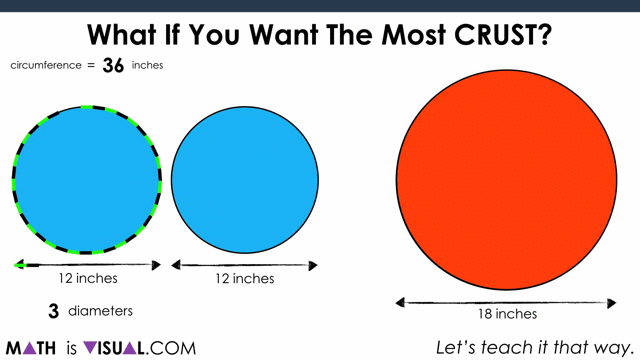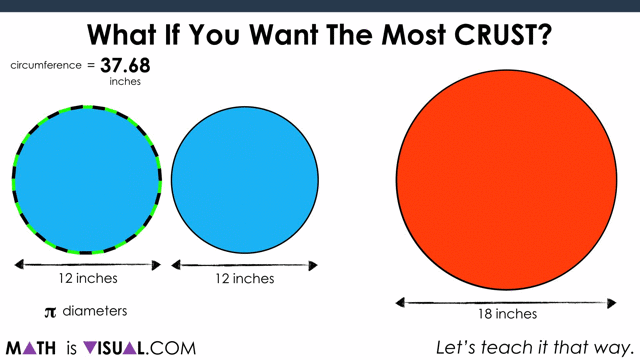
As you see in the video, the winner in this case is the 2 medium pizzas.

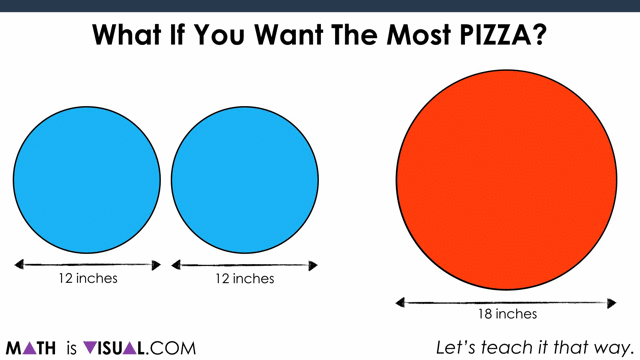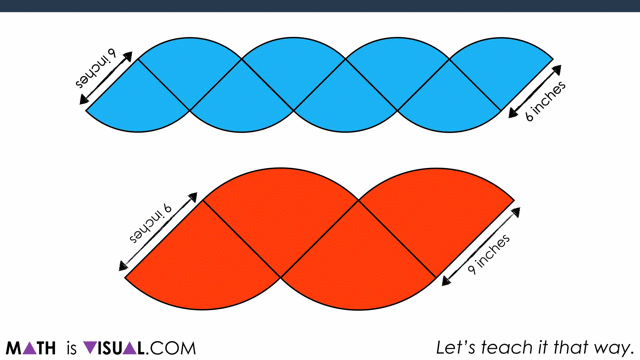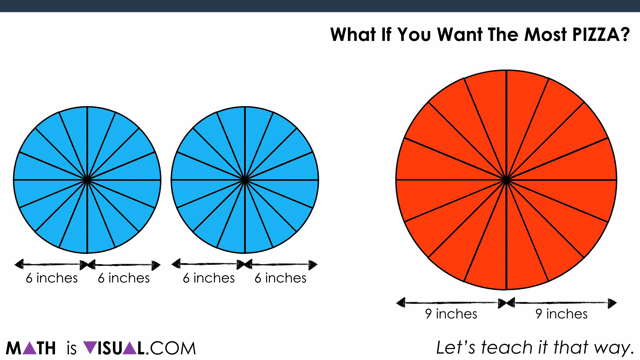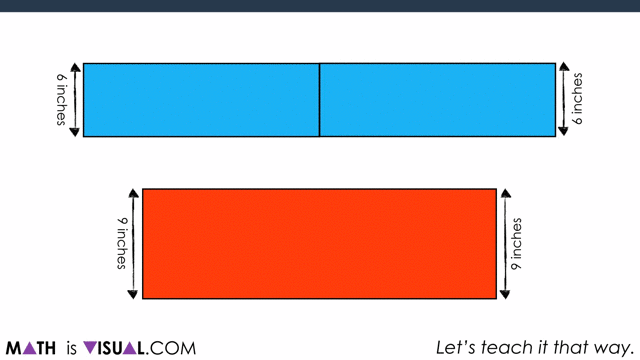
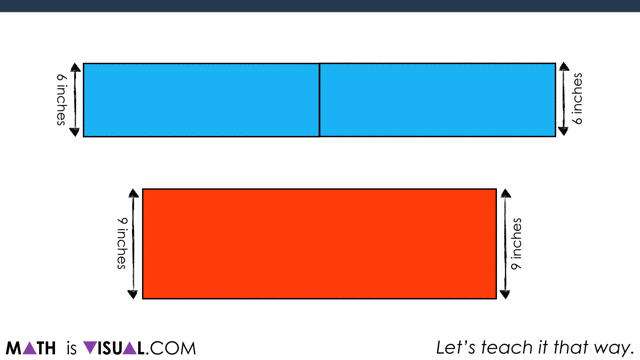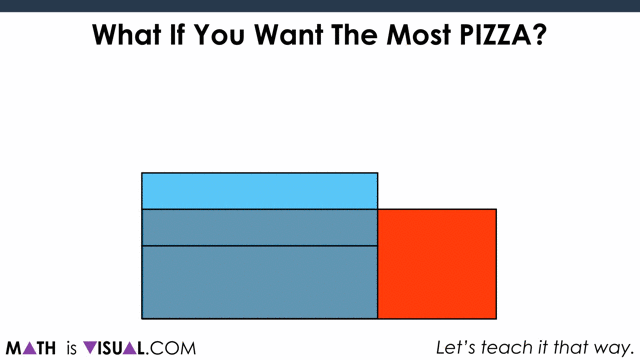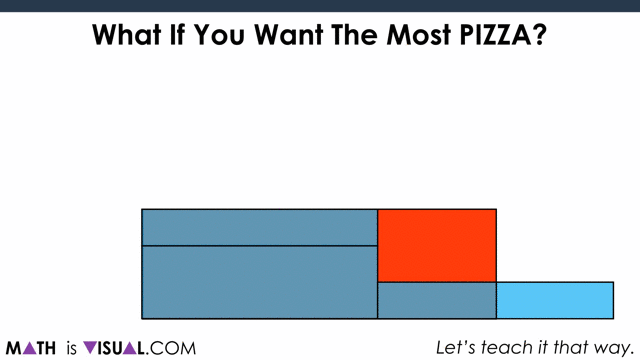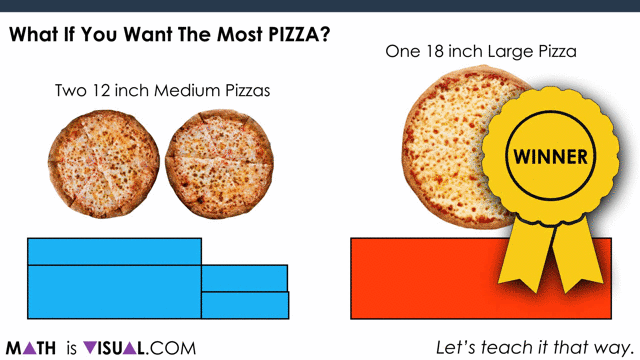
What If You Want The Most Pizza?

Next, let’s ask students if they would still stick with 2 mediums if they want the most pizza.

Again, have them convince their neighbours.

When consolidating, you can use two versions. One is purely spatial involving partitioning by creating a parallelogram out of the circles and then “covering it up“:

Now, to show covering it up:

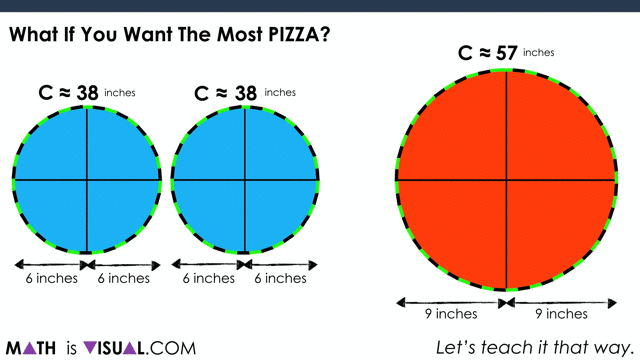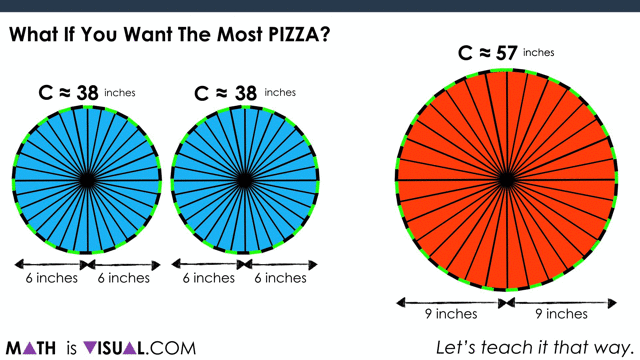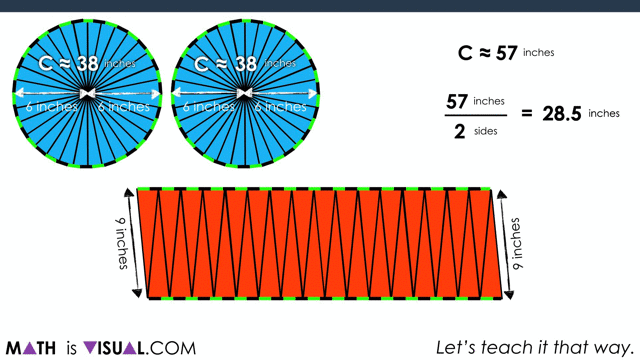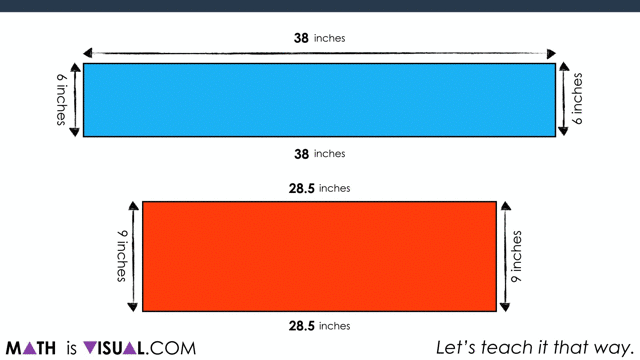
Students can also do this using measurements, noting that half of the circumference of each circle ends up being the “length” of the resulting parallelogram.

In the video, you also see some number sense strategies being used to promote number fluency.

For example, we decompose the slide length of 38 inches to 10 + 10 + 10 + 8 to make multiplication easier without resorting to a standard algorithm or a calculator:

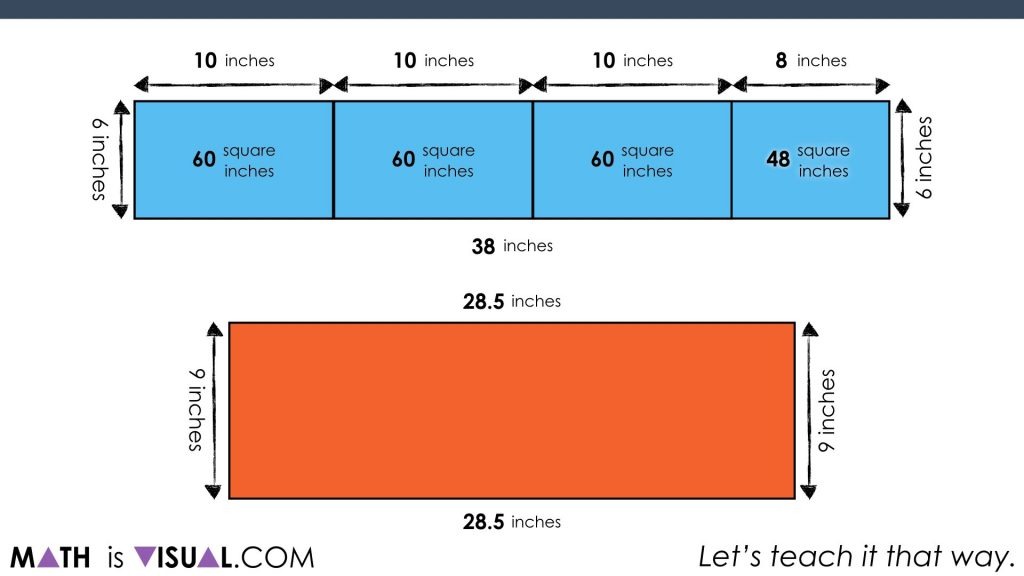
We also use a compensation strategy for the rectangle of the large pizza by multiplying 28.5 inches by 10 inches (instead of 9) and then subtract 1 group of 28.5 inches afterwards:

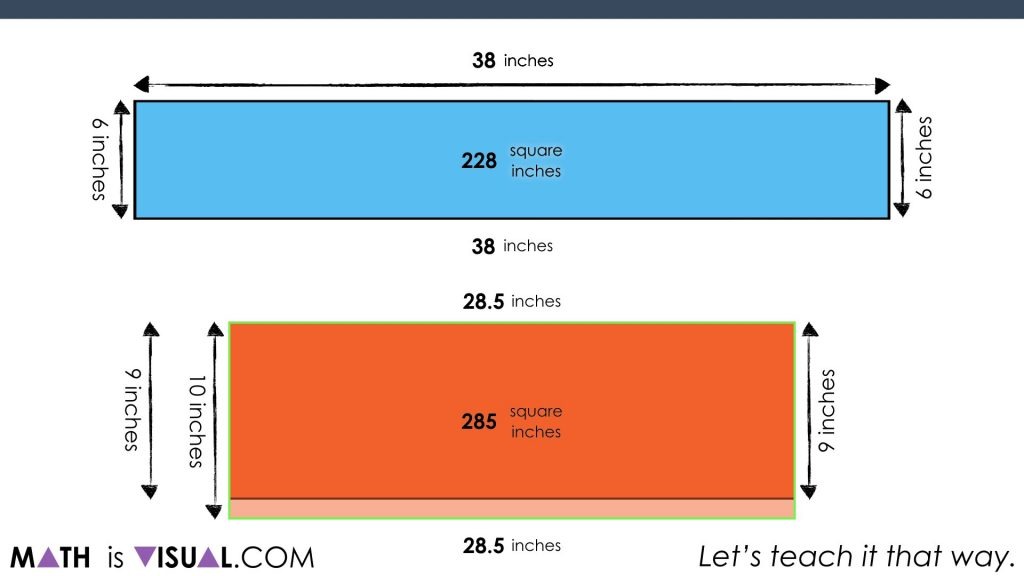
As you can see, in the end, the large pizza is the winner:

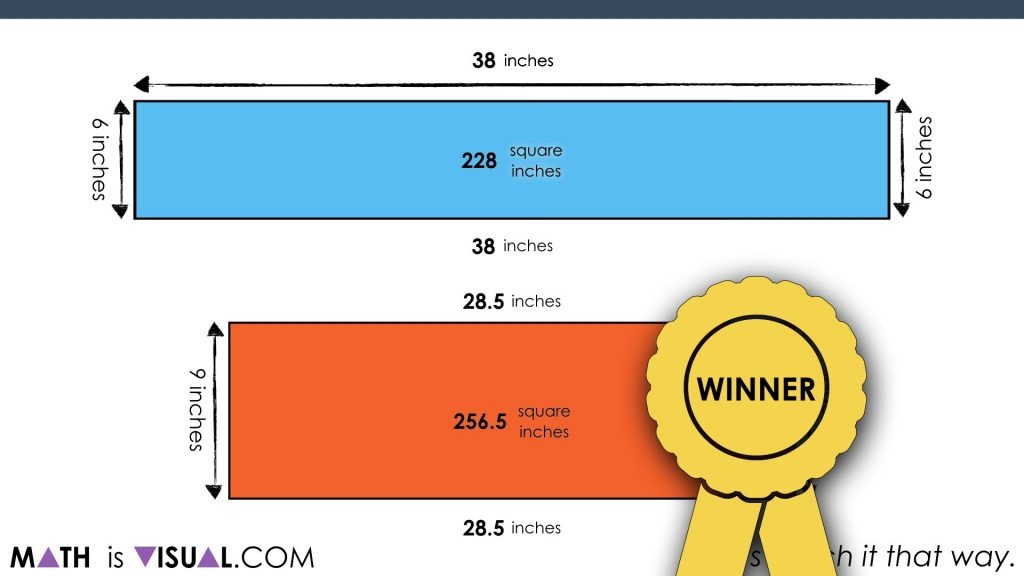
Go ahead, have some FUN with your students as we learn the area of a circle. Remember, it’s all about the rectangle in the end!

How’d It Go?

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.

Dive into fun math lessons that focus on concepts first with a goal of also developing procedural fluency throughout.