Visualizing The Area of a Triangle Formula

July 20, 2022

19,290 views

4 min read

Build an understanding of the area relationship between triangles and rectangles through this set of Area of a Triangle Number Talk Prompts.

In This Set of Visual Number Talk Prompts…

Students will emerge the formula for the area of a triangle by taking half of the area of a rectangle.

Intentionality…

This visual math talk and purposeful practice serve to develop a deeper understanding of the following big ideas.

The area of a rectangle can be determined by multiplying the length of its base by the length of its height;
The area of a rectangle is used to determine the area formulas for other polygons;
Using “base” and “height” rather than “length” and “width” can support student understanding when determining the area formulas for triangles and all quadrilaterals;
A parallelogram is any quadrilateral with two sets of parallel sides;
A rectangle is a parallelogram;
The relationships between rectangles, parallelograms, and triangles can be used to determine area formulas;
Any triangle can be doubled to create a parallelogram;
Congruent shapes have the same size and shape, but not necessarily the same orientation.

Visual Number Talk Prompt

Begin playing the visual number talk prompt video and then be ready to ask students:

Calculate the area of each triangle in square metres.

Craft a convincing argument without the use of a calculator.

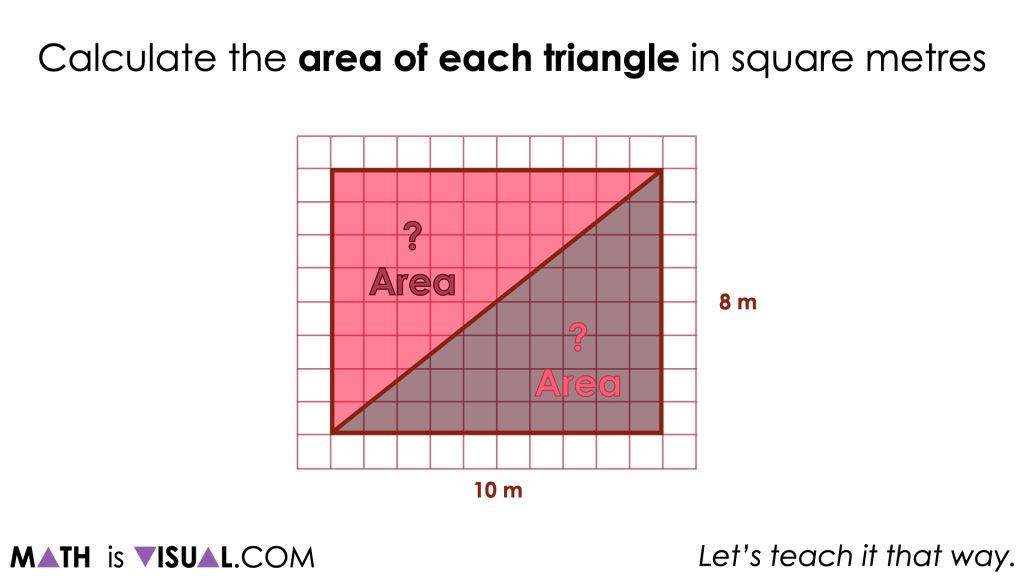
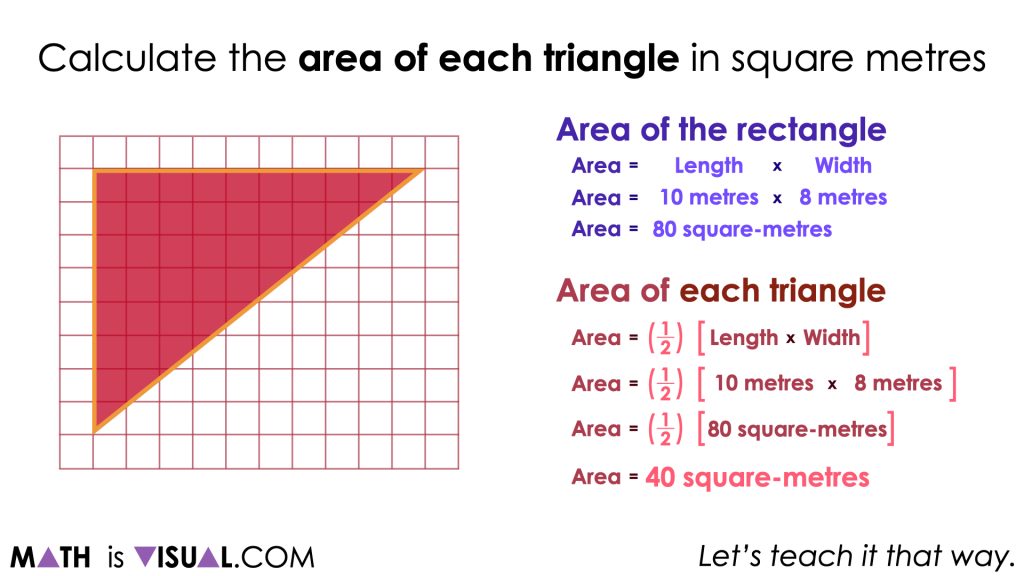
$area of the triangle$

As you may immediately notice, we have given students two congruent triangles and have conveniently arranged them such that together, they create a rectangle. This is intentional to ensure that all students explicitly see that every rectangle can be partitioned diagonally into two congruent triangles. From this visual math talk prompt, we hope to reiterate that partitioning any rectangle diagonally into two congruent triangles will result in each triangle having half of the area of the rectangle.

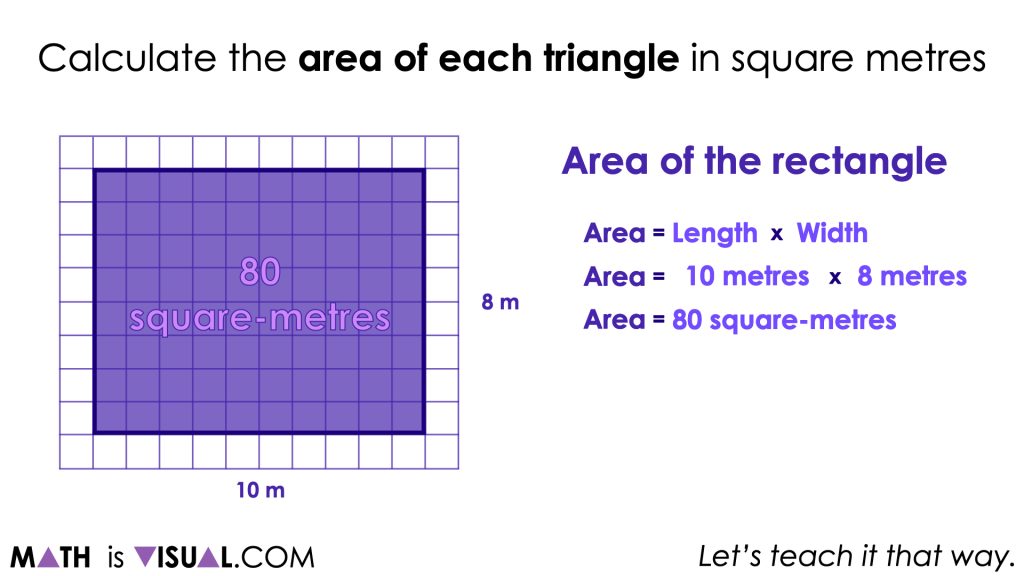
$area of the triangle$

Therefore, it may feel intuitive to some students to first find the area of the rectangle and simply half that quantity to determine the area of each of the resulting triangles.

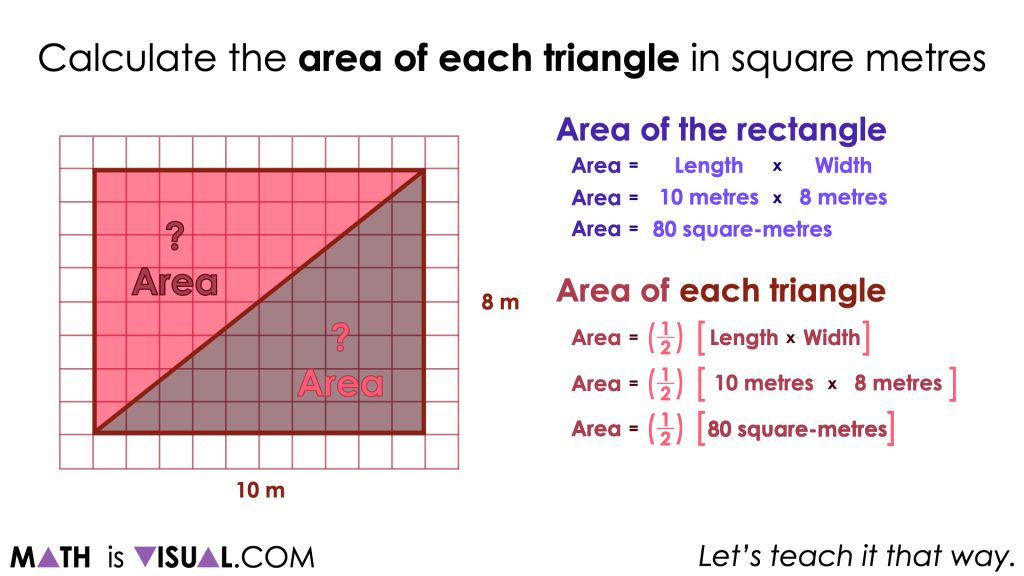
$area of the triangle$

While some students may perform the operation of taking half of the area of the rectangle (or dividing the area by 2), it is likely that many will not naturally write their thinking down symbolically as you see on the right of the screen. The goal here is not necessarily to ensure that all students “copy down” the formula, but rather so they can make a connection between the intuitive actions they had completed to find the area of the triangles to the symbolic representation of that same thinking.

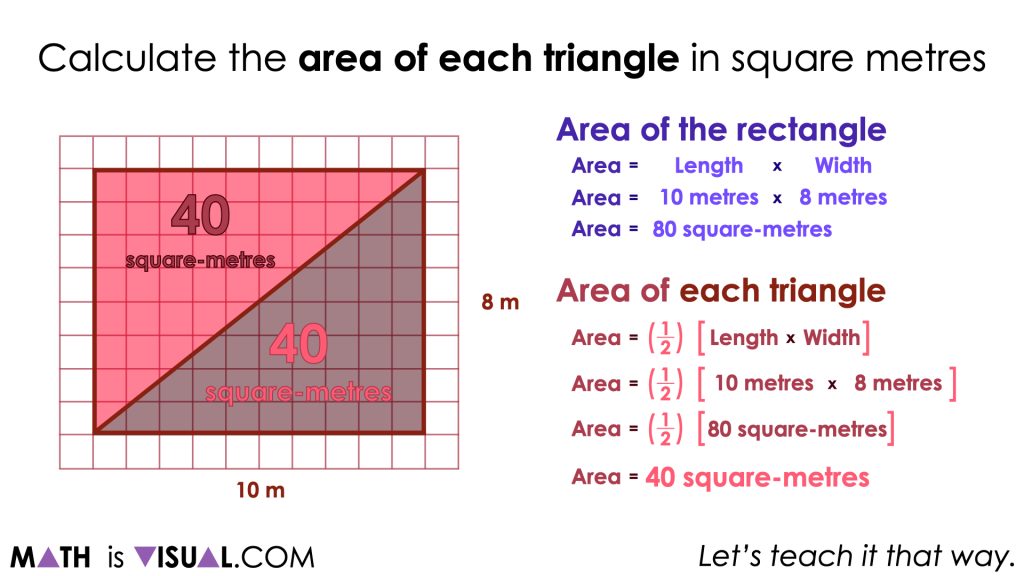
$area of the triangle$

It is important to explicitly highlight that the two triangles that were created by partitioning the rectangle diagonally result in congruent triangles as this may not be obvious to all students immediately.

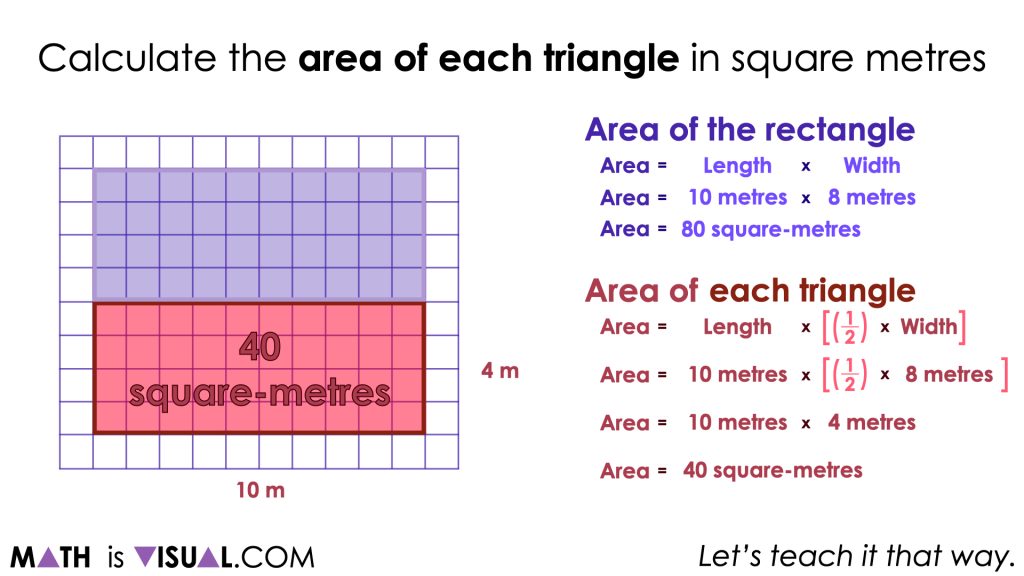
$area of the triangle$

It could also be helpful to show students that despite taking half of the area of the rectangle (or dividing the area by 2) revealing the area of each congruent triangle, the same operation can be done to determine the area of other congruent shapes that result when partitioning the original rectangle in half. For example, horizontally partitioning the rectangle into halves allows us to complete the same mathematical operation to reveal the same area.

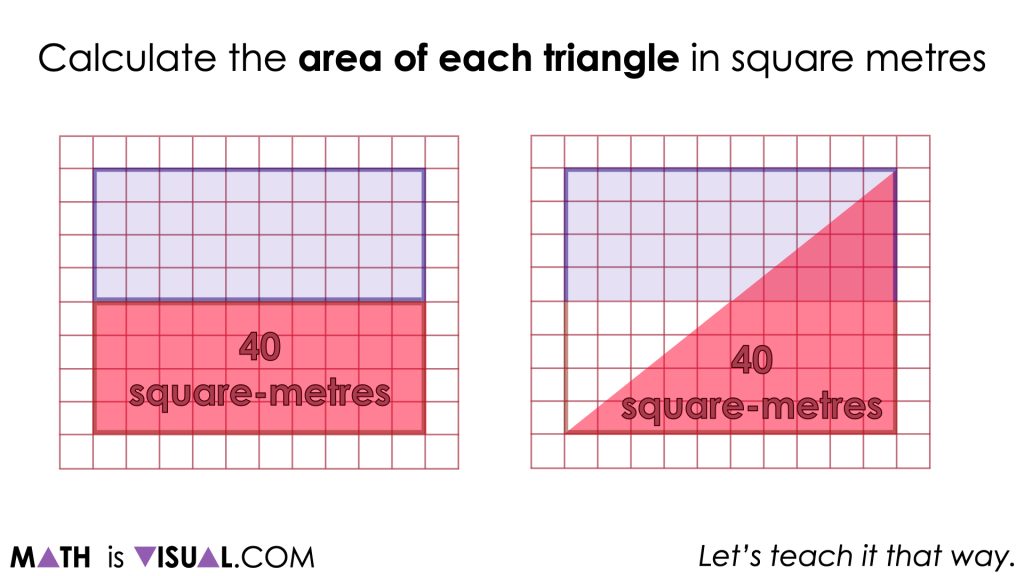
$area of the triangle$

This idea helps to highlight the fact that representing mathematical thinking of area symbolically can strip away information about how the units of area are arranged (i.e.: as a rectangle, a triangle, or some other shape).

$area of the triangle$