In This Set of Visual Number Talk Prompts…
Students will emerge the formula for the area of a parallelogram by decomposing and recomposing into a rectangle with the same area.
Intentionality…
The math talk serves to develop a deeper understanding of the following big ideas.
- The area of a rectangle can be determined by multiplying the length of its base by the length of its height;
- The area of a rectangle is used to determine the area formulas for other polygons;
- Using “base” and “height” rather than “length” and “width” can support student understanding when determining the area formulas for triangles and all quadrilaterals;
- A parallelogram is any quadrilateral with two sets of parallel sides;
- A rectangle is a parallelogram;
- Any triangle can be doubled to create a parallelogram;
- Congruent shapes have the same size and shape, but not necessarily the same orientation;
- Any parallelogram can be decomposed and recomposed to build a rectangle with the same area.
Visual Number Talk Prompt
After a grid and a parallelogram appear on the screen, pause the video and share the following prompt:
Identify the base and height of the parallelogram and calculate the area in square-units.
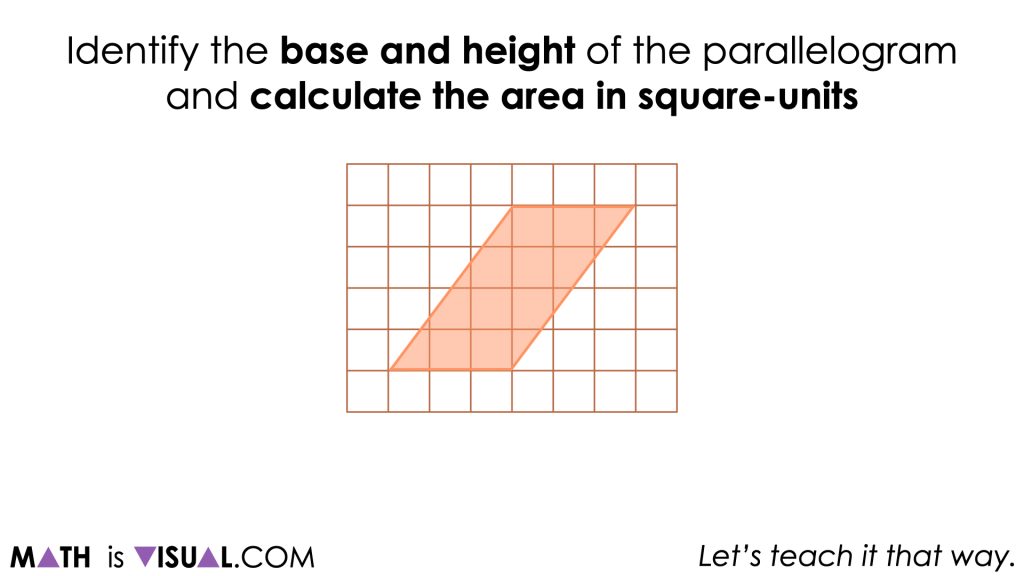
As we explore these visual prompts, we want students to begin visualizing the decomposition of each parallelogram and recomposition into a rectangle to drive home the connection between the area of a parallelogram and the area of a rectangle.
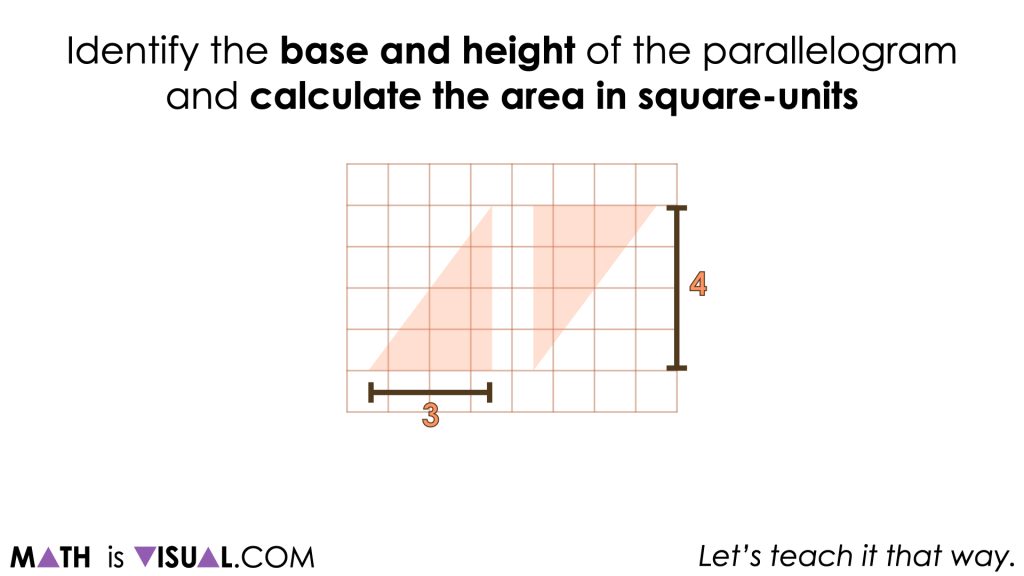
As students engage in this work, they will be able to quickly identify the base and height of a parallelogram and visualize both measures as the length and width of a rectangle with an equivalent area.
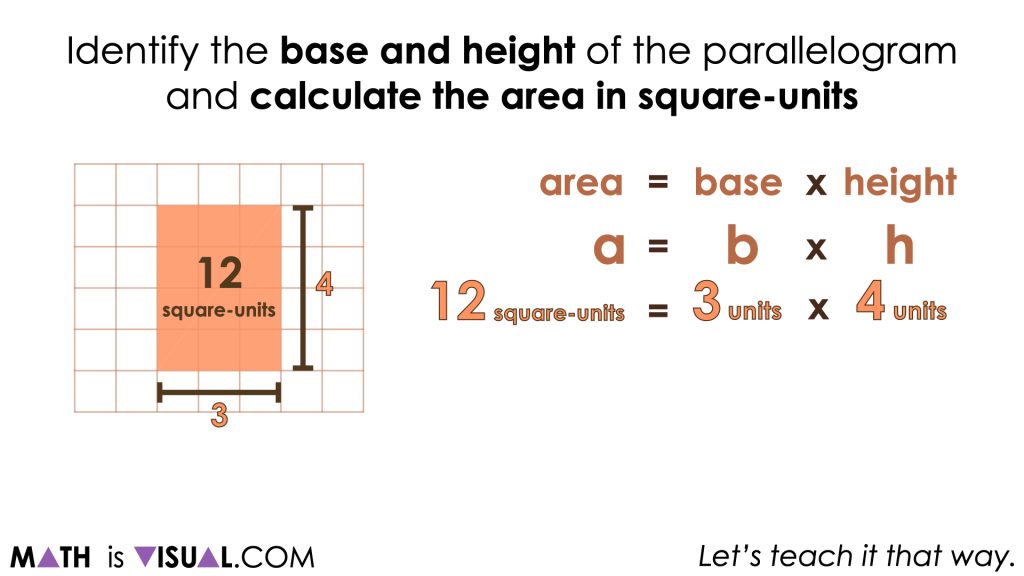
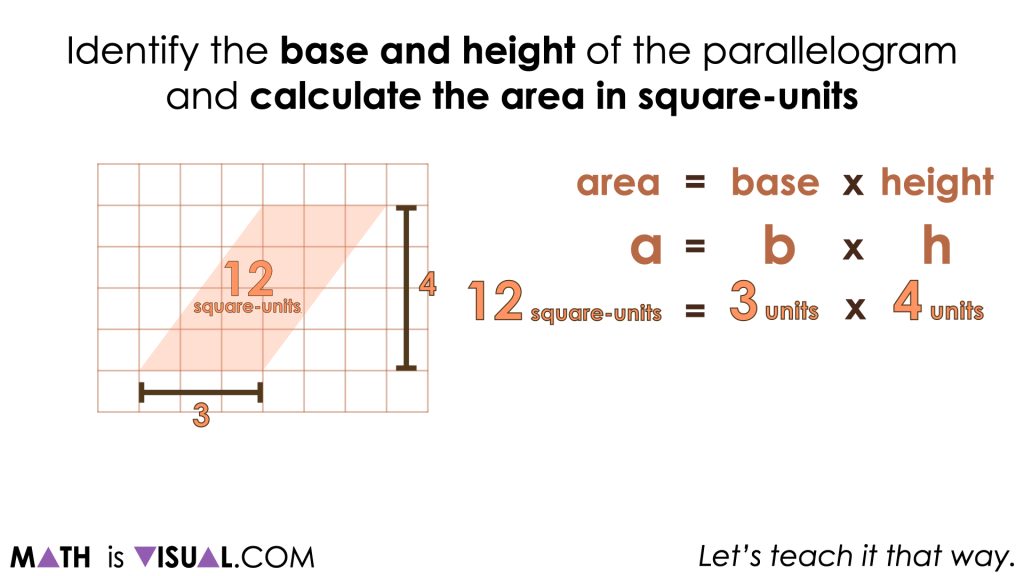
Repeatedly finding the area of a rectangle and seeing this quantity of square units as equivalent to the area covered by a parallelogram with the same dimensions is important to strengthen the conceptual understanding of students and allow them to work towards building procedural fluency.
Want to Explore These Concepts & Skills Further?
Three (3) additional number talk prompts are available in Day 4 of the Covering Ground problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.

Add comment