In this series of Math Is Visual Prompts, students are given the opportunity to wrestle with the idea of area – in particular the area of a circle – through a “Would You Rather” situation.
This particular series of Visual Prompts were extended to be used as the 4th day in our Make Math Moments circle measurement problem based unit called Going In Circles! In the 8-day unit, you’ll emerge the idea of Pi, bump-into the formula for circumference of a circle, extend this thinking to area of a circle and engage in math talks and purposeful practice throughout.
As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and after consolidating in the classroom through student work.
Let’s get started…
Spark Curiosity: Would You Rather…
Ask students “Would You Rather two 12 inch medium pizzas or one 18 inch large pizza?” to spark curiosity and pause where indicated in this video.

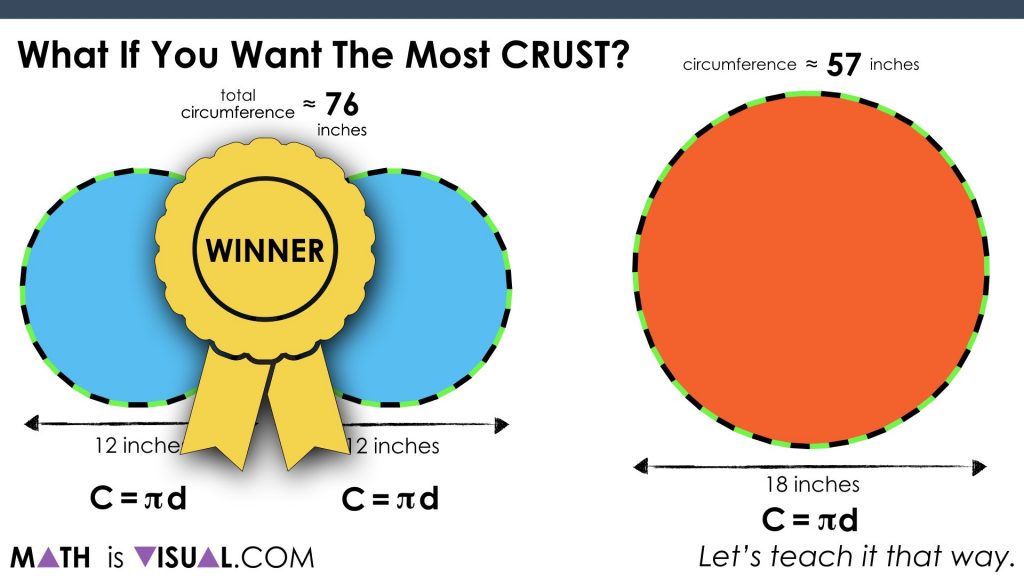
What If You Want The Most Crust?
After they all share out, challenge them to think about whether they want to change their answer if you were looking for the situation with the most crust:

At this point, we want them to start digging in. Be sure to ask them to convince their neighbours as we want to move beyond just gut shot guesses.
This is a great opportunity for students to “play” with the idea of circumference as it relates to the diameter of a circle. As they may (or may not) be aware, the ratio of the circumference to the diameter is approximately 3.14:1.
Yes, it is π:1!
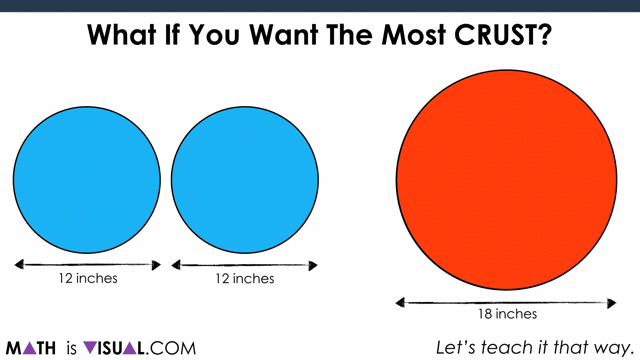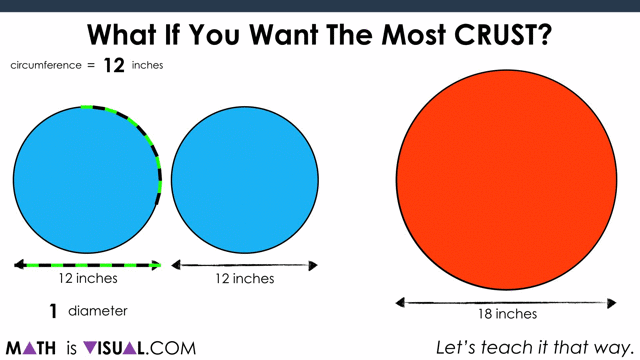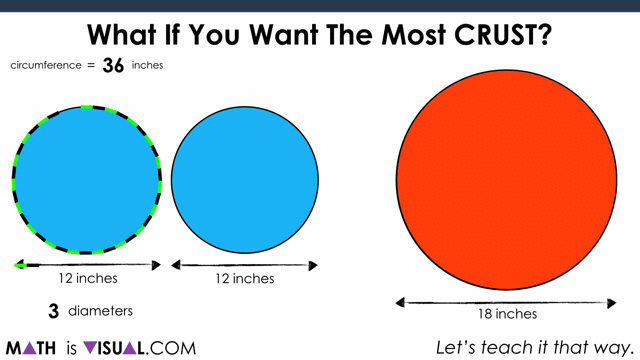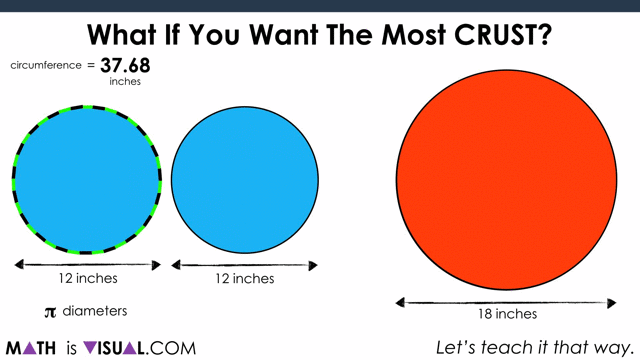
As you see in the video, the winner in this case is the 2 medium pizzas.
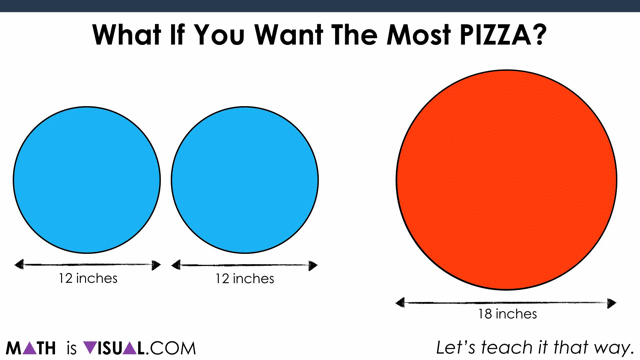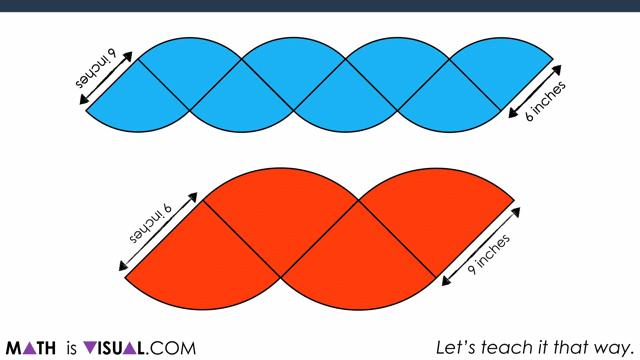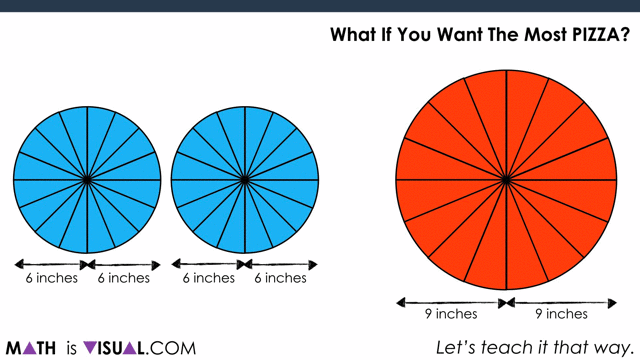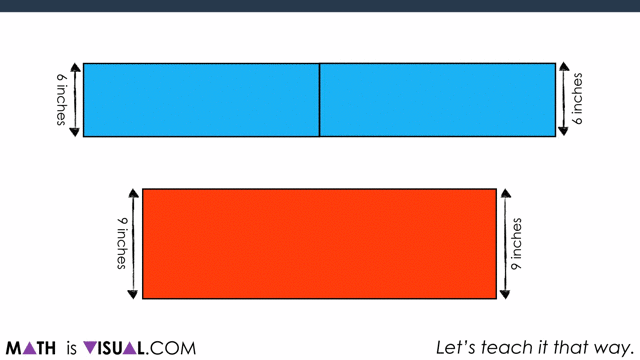
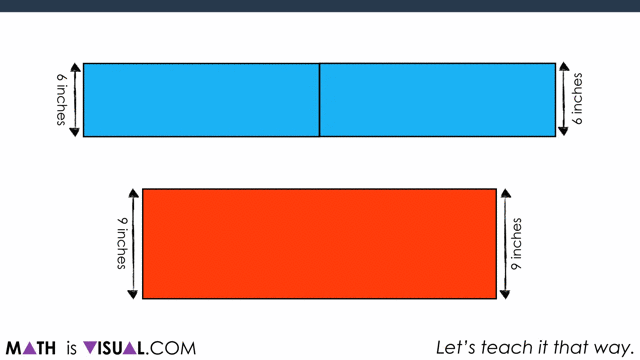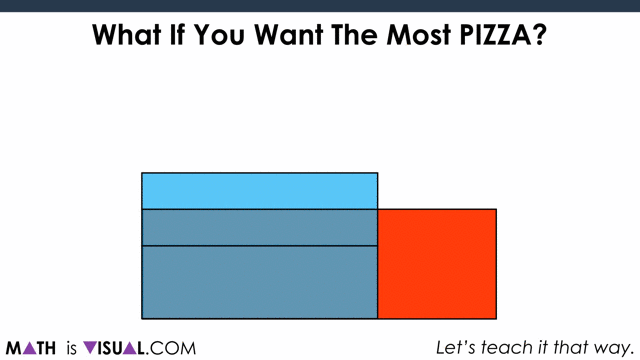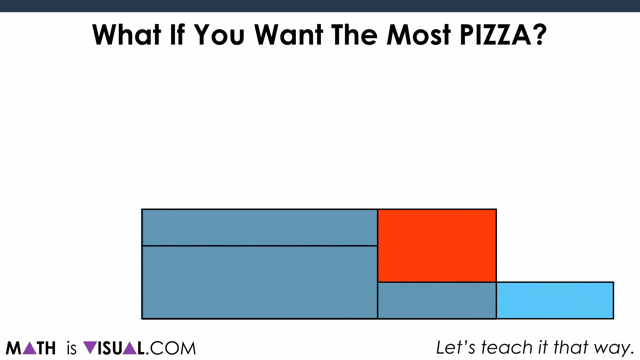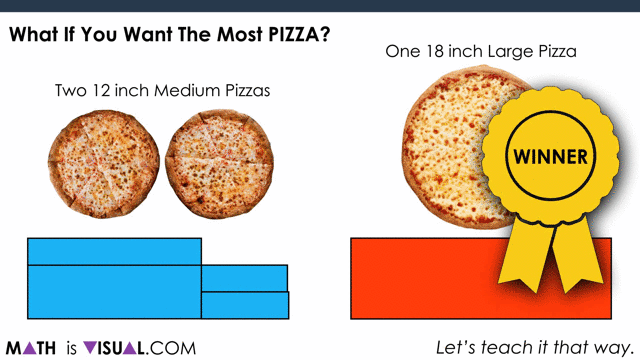
What If You Want The Most Pizza?
Next, let’s ask students if they would still stick with 2 mediums if they want the most pizza.

Again, have them convince their neighbours.
When consolidating, you can use two versions. One is purely spatial involving partitioning by creating a parallelogram out of the circles and then “covering it up“:
Now, to show covering it up:
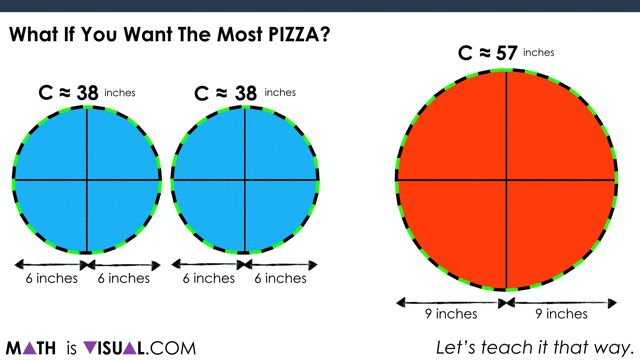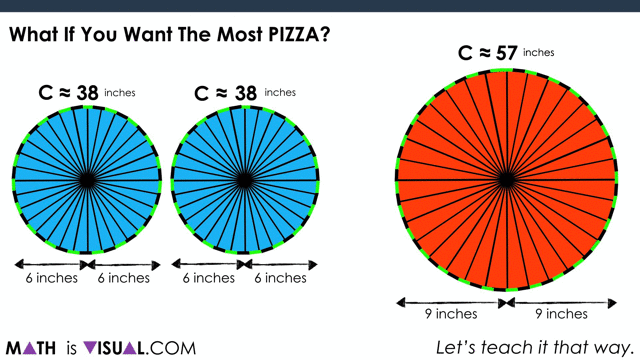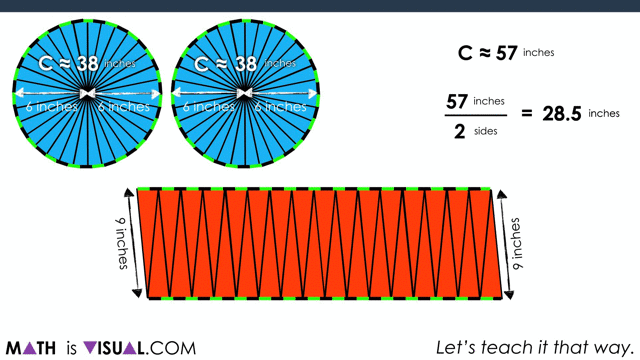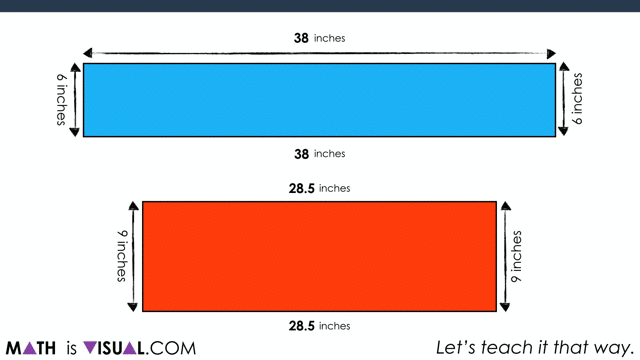
Students can also do this using measurements, noting that half of the circumference of each circle ends up being the “length” of the resulting parallelogram.
In the video, you also see some number sense strategies being used to promote number fluency.
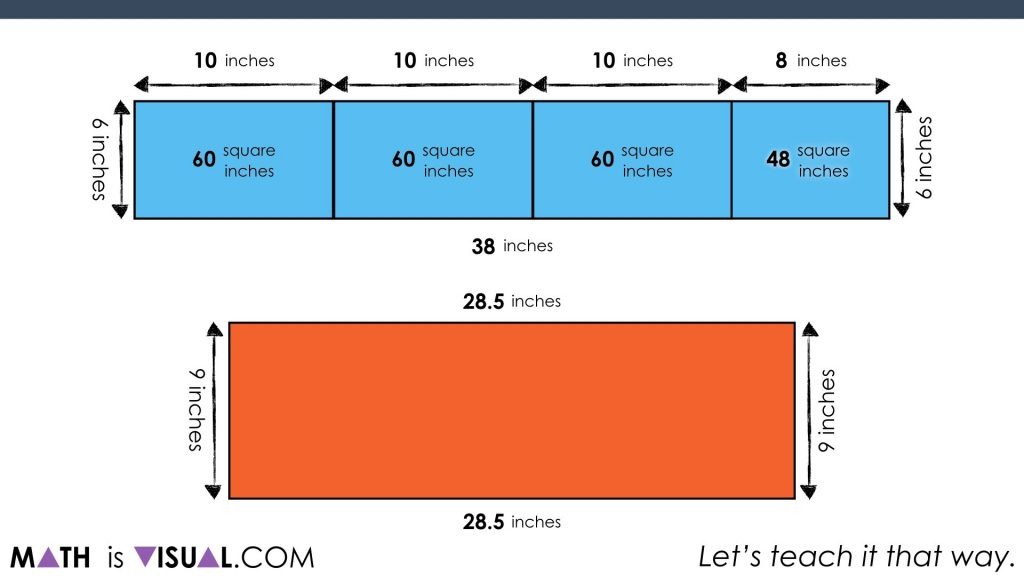
For example, we decompose the slide length of 38 inches to 10 + 10 + 10 + 8 to make multiplication easier without resorting to a standard algorithm or a calculator:
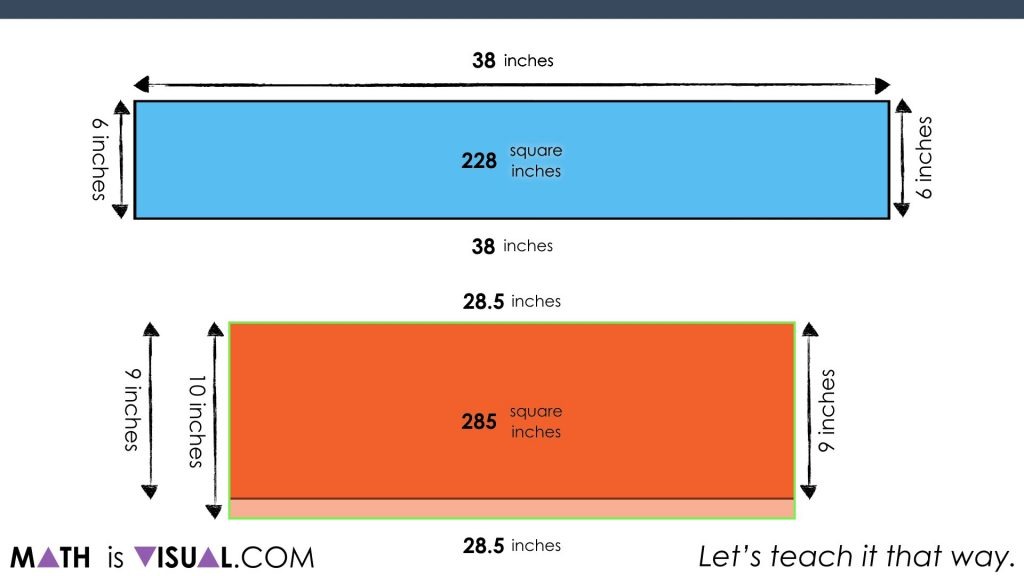
We also use a compensation strategy for the rectangle of the large pizza by multiplying 28.5 inches by 10 inches (instead of 9) and then subtract 1 group of 28.5 inches afterwards:
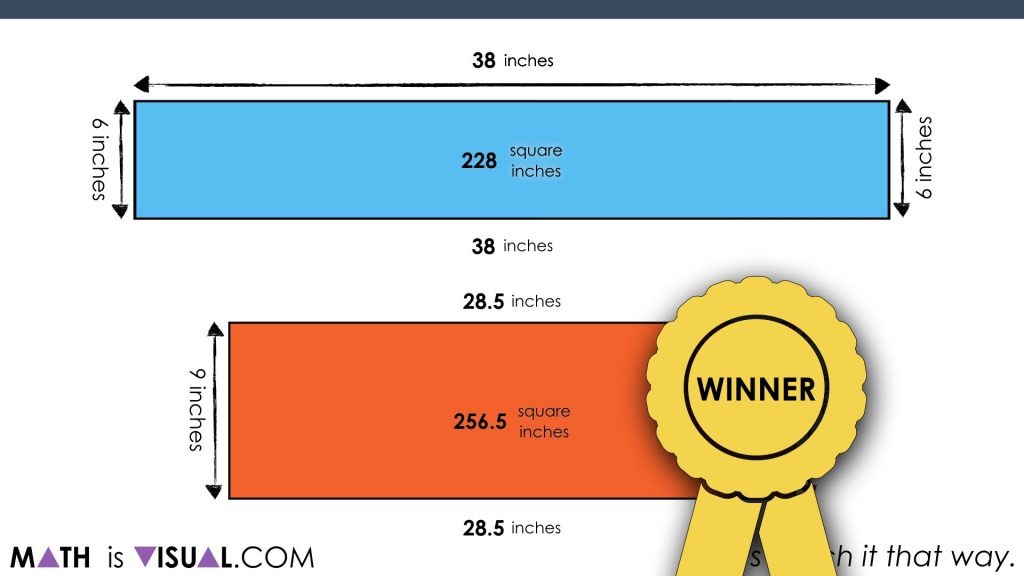
As you can see, in the end, the large pizza is the winner:
Go ahead, have some FUN with your students as we learn the area of a circle. Remember, it’s all about the rectangle in the end!
How’d It Go?
Thanks for watching and reading!
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.
Dive into fun math lessons that focus on concepts first with a goal of also developing procedural fluency throughout.
Is there sound for this video and my computer is just not picking it up? Love the video…….
Hi Robyn! All videos are “silent solution” videos where the facilitator is using the videos to allow learners to notice and wonder. You then get the opportunity to ask the purposeful questions. Never fear, your speakers work! 🙂
You could just calculate the area of the circles instead of all the convoluted shape manipulation.
Of course! Which would require you to use a formula, which was created through the manipulation of circles to more simple shapes like a parallelogram or rectangle!
Awesome visualizations Kyle. These videos are very precious for the students’ to see and then develop their own formule. Thanks
Thanks for stopping by and sharing your feedback! Hoping to keep on creating new visuals to help folks in their journey to conceptualizing mathematics!
These are terrific. Is there a way to watch without the ads popping up?
That’s odd. There shouldn’t be any ads on these videos?
Very interesting and helpful, I now understand why my kids are using/learning visual strategies instead of formulas at school. I could see the details, but not the big picture. Now I think I do, thank you very much for that. I’m looking forward to exploring your site with them.
So happy you stopped by! Let us know how it goes when you’re using the site with students!
As a teacher of Mathematics, I really appreciate these visuals. Only wish page wasn’t so crowded with ads.
Hi Sharlene!
Thanks for stopping by!
Can you help me understand which ads you’re referring to? On the video or on the page? We don’t have any ads on the page and I don’t think on the videos either?
Thank you, this is great and I don’t see ads. What do you suggest is the best way for us to show/share the visuals with our students? The answers are just below the pictures and I don’t want them to see these as I scroll through.
I’d encourage you to use the video at the top and pause throughout… the written text below is more facilitator moves.
Does that make sense?
Thanks Kyle. I used this today with my year 9 Mathematics class (first year of secondary school) and they were well engaged (mostly because it was pizza!). Some had not brought calculators to class, so the number sense strategies were very useful. There was a bit of questionning around the “exact” value of pi that is not likely to be resolved until year 13 Calculus when we derive the formula for area of a circle from integration of the circle relation.
[…] Kitchen Lab: Discuss: “What do you need to know in order to decide which pizza choice would give you the most pizza instead of the most crust?” *Invite them to investigate their solutions: “Let’s investigate!” * If you need extended examples, use the Math is Visual link. […]
This is ahead of my Grade 5 learners who are struggling even at this level. But I KNOW pizza would definitely grab their attention! I shall be saving these great visual lessons for them. Plus, these give.me “ideas” that I could perhaps use for other Maths concepts at their current level. Thank you for brilliant work, Kyle…and for be willing to share this with us and our learners.