In This Set of Visual Number Talk Prompts…
Students will explore modelling multiplication and solving multiplication problems using the array model. .
Intentionality…
Students will engage in a string of related problems through a math talk to develop a deeper understanding of the following big ideas
- Multiplication can involve determining the total quantity given the number of equal groups and the size of each group;
- The order of the numbers in a multiplication sentence does not matter (commutative property);
- The strategy of doubling and halving is possible due to the associative property of multiplication;
- The distributive property of multiplication supports the strategy of partial products (where one or both factors can be decomposed over addition or over subtraction).
String of Related Problems
Present the following multiplication sentences one at a time. Encourage students to describe a context that could be represented by each sentence. For example, the arrangement of windows on the front of a building.
These particular factors were selected to encourage partial products as a strategy for multiplying two digit by two-digit numbers using the array model.
Consider using a digital tool where the quantities within the array are concrete and countable when modeling student thinking.
10 x 10
10 x 6
3 x 10
3 x 6
13 x 16
Consider watching this silent solution animation to help you prepare to facilitate this math talk utilizing an array. In this video, you will see how the multiplication sentence 13 x 16 can be decomposed using the array model.
Visual Number Talk Prompt
Students Prompt:
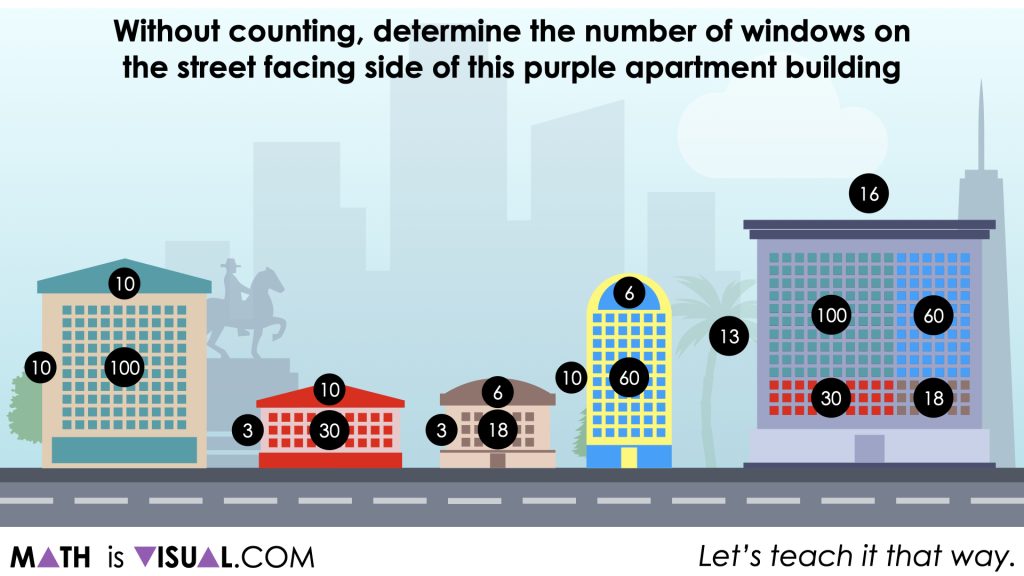
Without counting, determine the number of windows on
the street facing side of each apartment building.
On each of the buildings, students are given the number of rows and columns of windows and they are all (likely) known facts for students.
The goal is for students to calculate the partial products or the number of windows in “parts” of a much larger apartment building that is not a known multiplication fact.

While students may not immediately notice, if they instinctively begin to decompose the factors into smaller, more accessible quantities for multiplying, they may recognize that the number of windows on the first four (4) apartment buildings is actually equivalent to the total number of windows on the larger building.

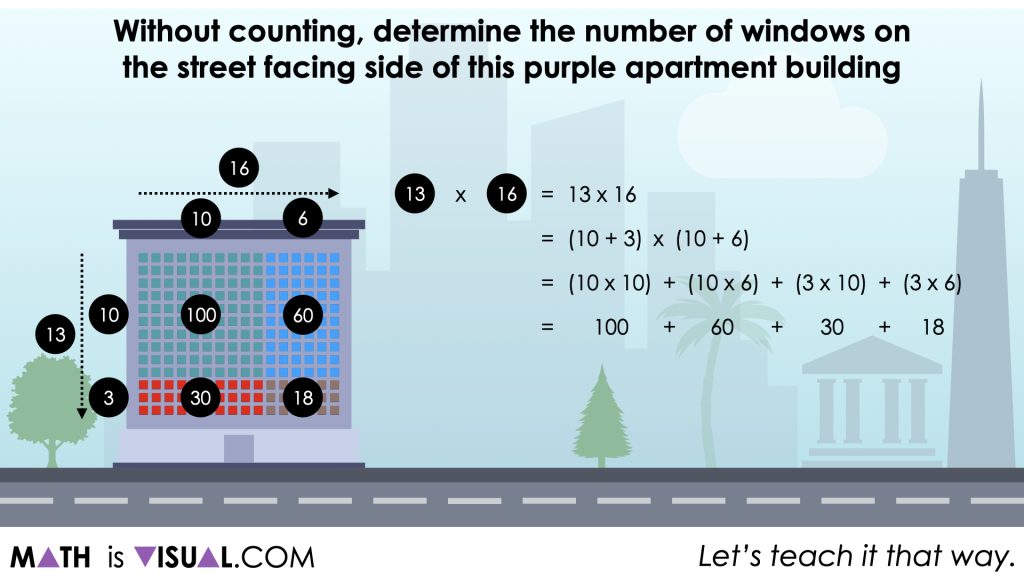
For example, if students decompose 13 rows into (10 + 3) rows and 16 columns into (10 + 6) columns, the resulting partial products will be:
10 x 10
10 x 6
3 x 10
3 x 6
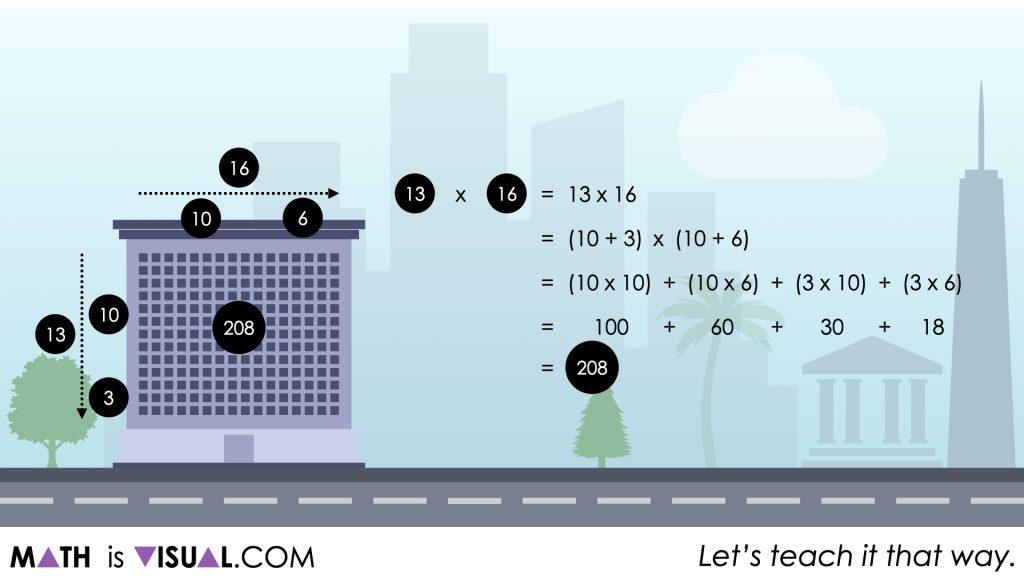
These smaller rectangular arrays can be recomposed to cover the large 13 x 16 array that represents all of the windows on the street facing side of the purple building.
Although it might not be obvious initially, it is important to note that the standard algorithm for multiplication is essentially leveraging the same partial products strategy that works due to the distributive property of multiplication.
Despite the fact that we are sharing this strategy in a horizontal fashion, the traditional “stacking” method for multiplying 2-digit by 2-digit numbers results in the exact same partial products.
It is also worth noting that this method that emerges quite naturally when students are leveraging an array model to multiply unfriendly numbers is often taught later in middle school and algebra 1 courses as “FOIL” in order to multiply binomials.
Consider reading about the Progression of Multiplication to get a more thorough sense of how the distributive property, partial products and the standard algorithm are connected.
Want to Explore These Concepts & Skills Further?
Two additional number talk prompts are available in Day 4 of the Stack ‘Em Up problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.



Add comment