In This Set of Visual Number Talk Prompts…
Students will explore modelling multiplication and solving multiplication problems using the array model. .
Intentionality…
Students will engage in a string of related problems through a math talk to develop a deeper understanding of the following big ideas:
- Multiplication can involve determining the total quantity given the number of equal groups and the size of each group;
- The order of the numbers in a multiplication sentence does not matter (commutative property);
- The strategy of doubling and halving is possible due to the associative property of multiplication;
- The distributive property of multiplication supports the strategy of partial products (where one or both factors can be decomposed over addition or over subtraction).
String of Related Problems
Present the following multiplication sentences one at a time. Encourage students to describe a context that could be represented by each sentence. For example, bottles in shelved cases of orange juice.
These particular factors were selected to emerge doubling and halving as a multiplication strategy.
All four multiplication sentences of this string are a set. It would be helpful to model student thinking using an array. Consider using a digital tool where the quantities within the array are concrete and countable.
8 x 14
4 x 28
2 x 56
1 x 112
Consider watching this silent solution animation to help you prepare to facilitate this math talk utilizing an array and open array.
Visual Number Talk Prompt
Students Prompt:
How many bottles are there?
Craft a convincing argument without the use of a calculator.
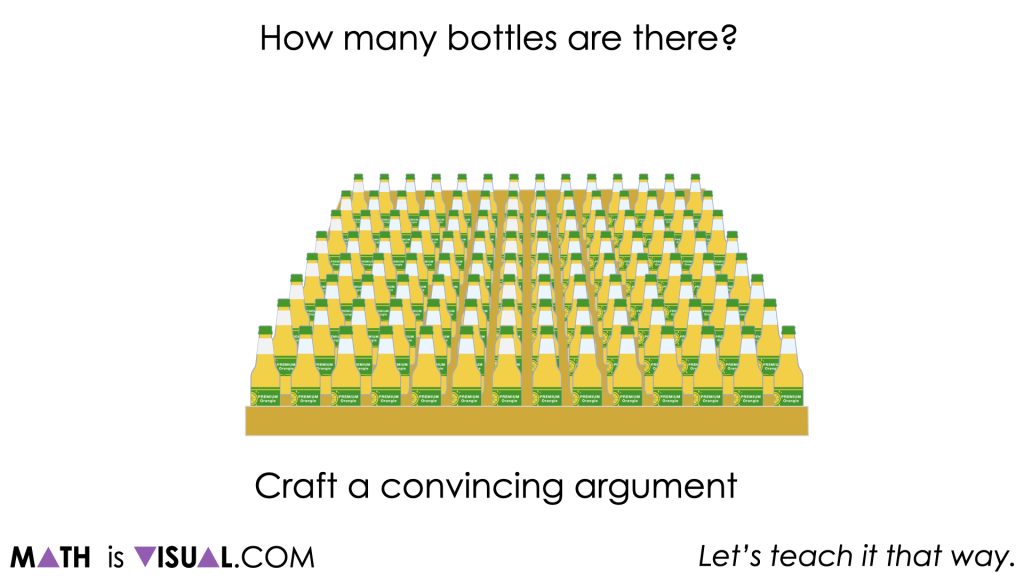
Similar to Day 1 of the Stack ‘Em Up problem based unit, students will be presented with a crate of drink bottles organized in an 8 x 14 multiplication array and will be tasked to determine how many bottles there are in total.
Since we are aiming to build fluency and flexibility multiplying one- and two-digit numbers we are going to ensure students are not leveraging the calculator as a tool.
As the facilitator, we are going to do our best to work from an array or open array (or area model) to highlight the strategies students are using to multiply these two factors.
Some students may choose to employ a doubling and halving strategy such as halving the 8 rows and doubling the 14 columns which employs use of the identity property (i.e.: any quantity multiplied by 1 keeps its identity or remains unchanged) and our understanding of fraction equivalence (i.e.: 1 = 1 whole = 2 halves = 2 one-halves) and the associative property to reassociate one-half with the 8 rows and 2 with the 14 columns.
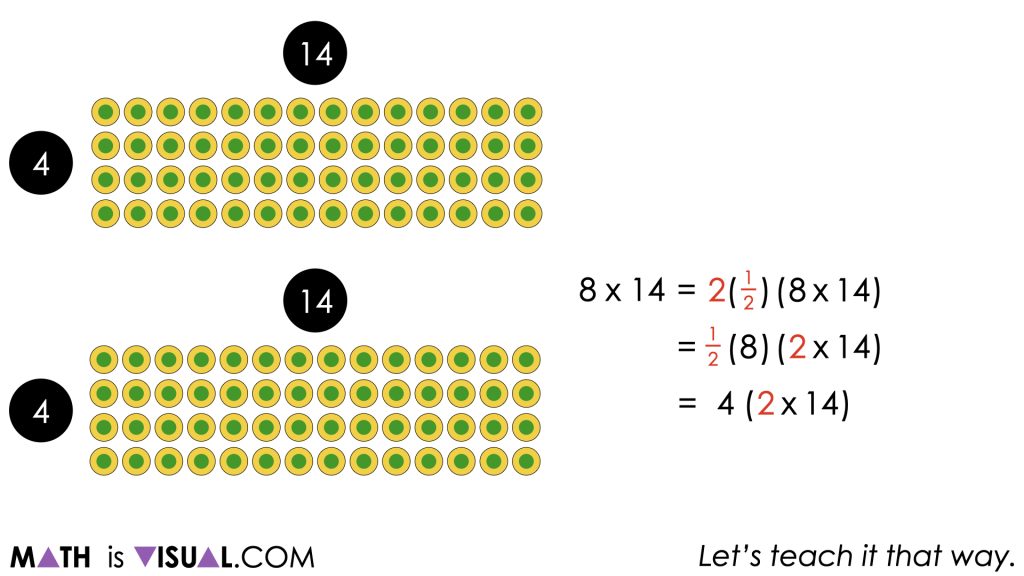
This use of the associative and commutative properties allows us to see that 8 rows of 14 columns is equivalent to 4 rows of 28 columns.
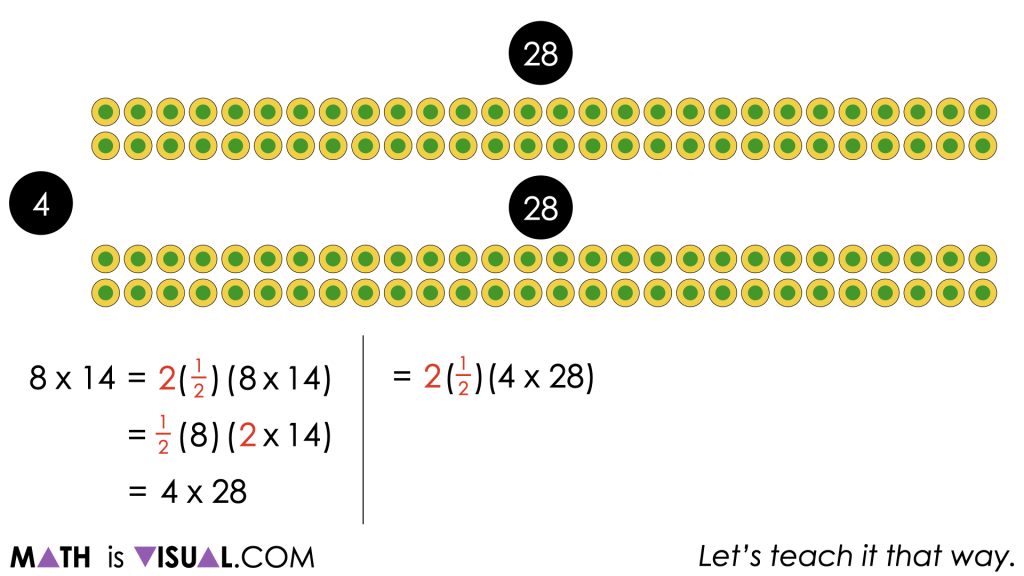
Of course, these visuals can support your facilitation of this visual number talk, but it would be most effective if the facilitator draws the models both as arrays or area models and represents symbolically as the thinking emerges.
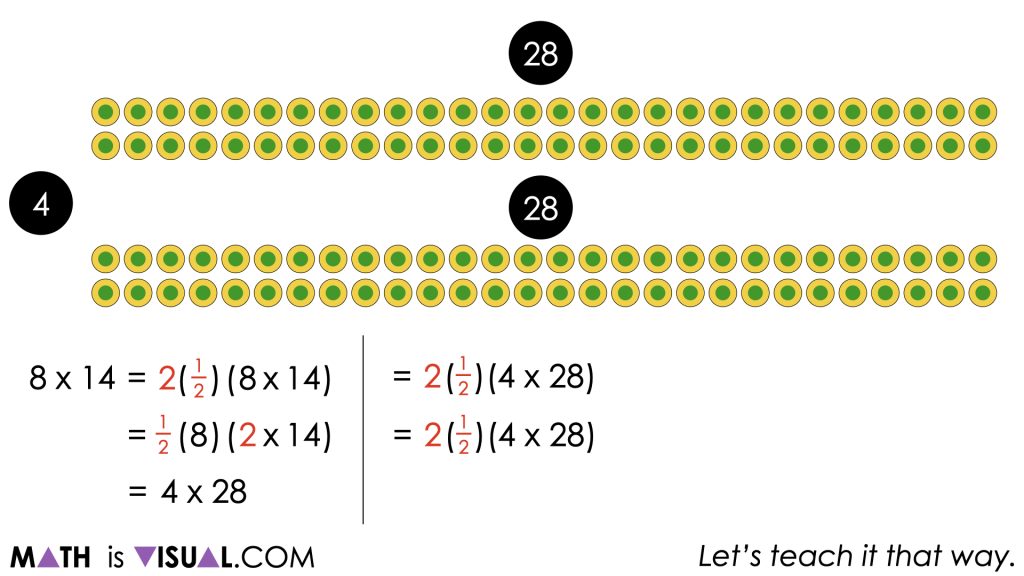
It is important for you to also determine how far symbolically you believe is beneficial for students given their current entry point. The symbolic representation here is more helpful for educators to understand what is actually happening through the use of the identity, commutative and associative properties.
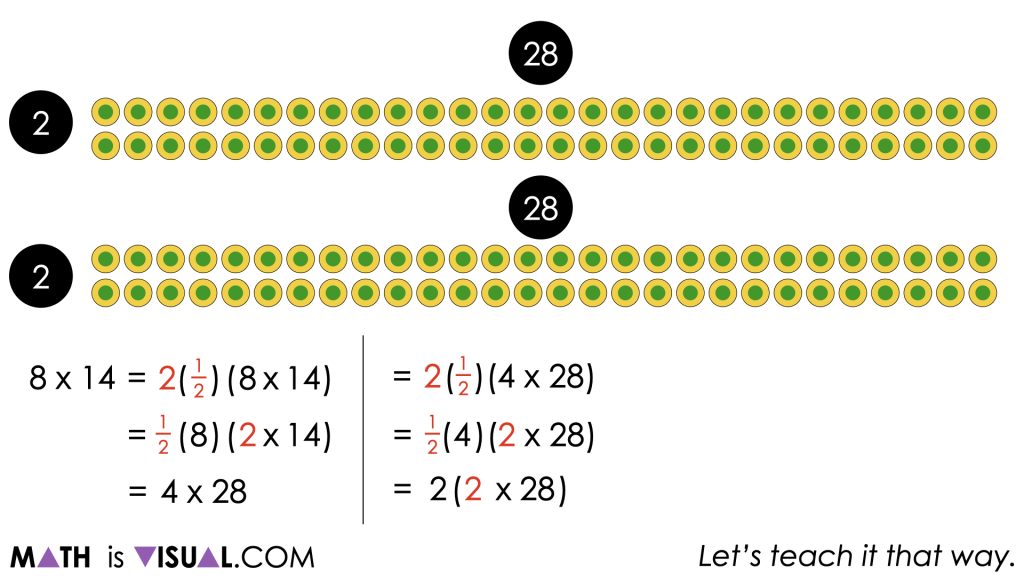
A student who is using a doubling and halving strategy can continue to use this strategy to make one of the factors smaller and smaller and one of the factors larger and larger until they are comfortable determining the product.
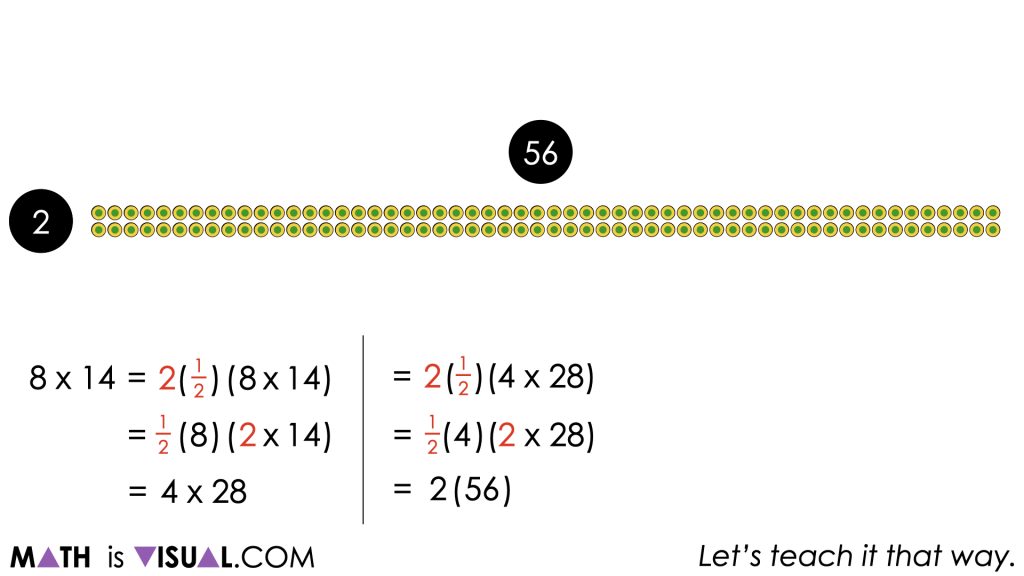
A student who continues to utilize this strategy will eventually arrive at a 1 by 112 array which results in a total of 112 bottles.

It should be noted that some students may choose to leverage the distributive property instead by breaking down 8 x 14 into 8(10 + 4) or some other variation that decomposes the factors down into more manageable chunks. This approach should also be modelled with an array and/or area model.
Want to Explore These Concepts & Skills Further?
An additional number talk prompt is available in Day 2 of the Stack ‘Em Up problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.

Add comment