Understanding Area of a Triangle Conceptually

In this Math Is Visual Prompt, students are given the opportunity to wrestle with the idea of area – in particular the area of a triangle – through a concrete and visual set of curious experiences. In order to maximize the concreteness of this activity, my suggestion is for square tiles or linking cubes to be out and available and have students try to make their estimates using the concrete materials. Also, using paper cut out triangles to decompose and recompose between triangles and rectangles is super helpful.

Let’s get started…

Spark Curiosity: What Do You Notice? What Do You Wonder?

Ask students “What do you notice? What do you wonder?” to spark curiosity and pause where indicated in this video.

Here’s an image of what students/children will be looking at when you are instructed to pause the video:

After students share what they notice and wonder, you can then show them the next portion of the video until you’re instructed to pause.

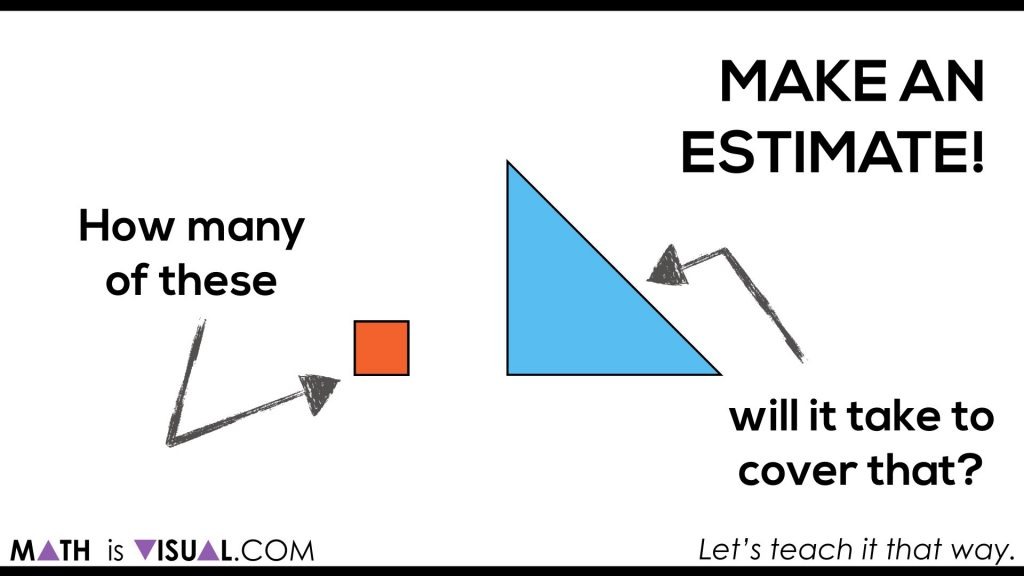
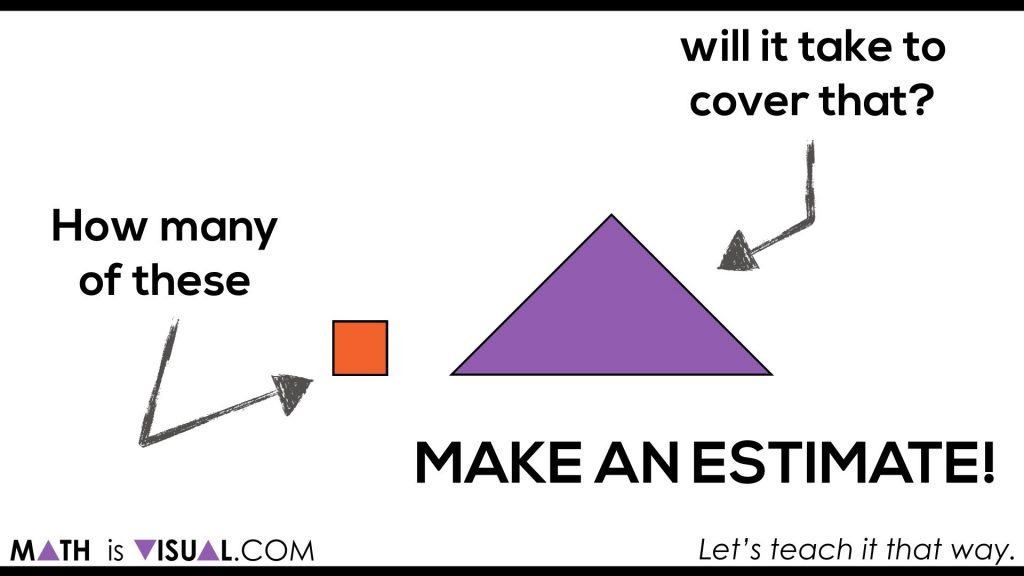
Here, students are now able to go ahead and try to make an estimate using spatial reasoning skills only. Having manipulatives out is a huge help. You could also simply cut out squares and have them try their best to represent based on what they see in order to help them build their diagrammatic skills and manipulation skills.

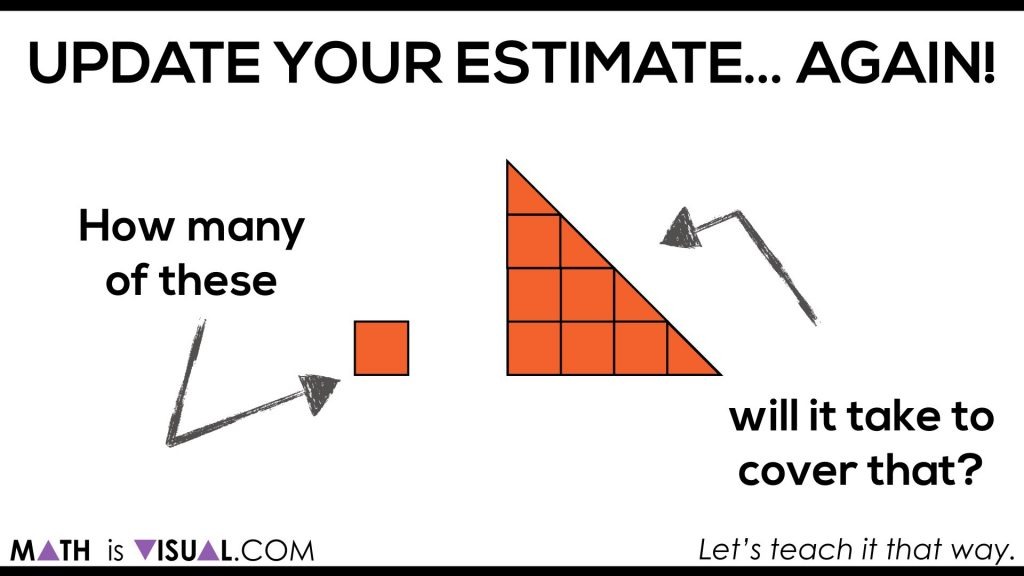
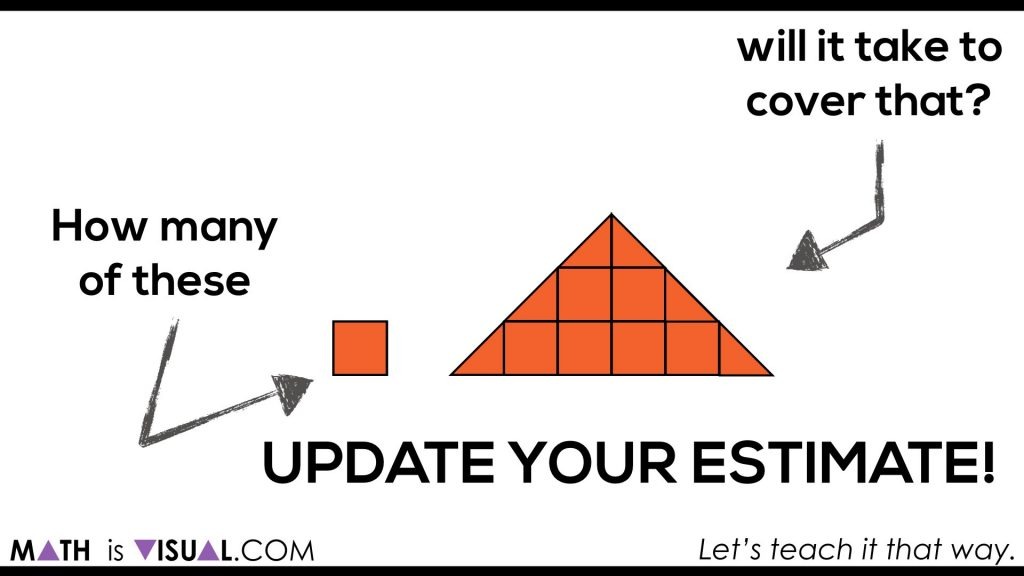
In the video, you can pause after each “row” of the triangle is filled for students to update their estimates.

Give children some think time and have them CONVINCE you of their most recent estimate. Are any students willing to GUARANTEE their estimate is precise? How come?

Act 3: The Big Reveal

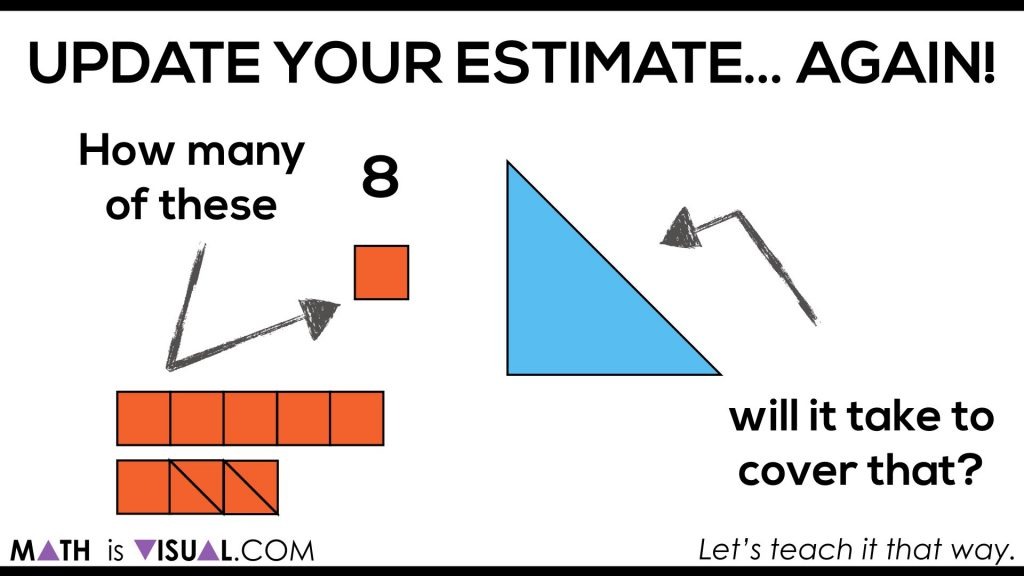
Students can now celebrate when they see how many squares can actually cover the rectangle:

In the video, each square is then counted out including the half squares into wholes:

Then, students are asked to estimate how many squares it would take to fill the rectangle when a second triangle that appears to be congruent to the first appears on the screen:

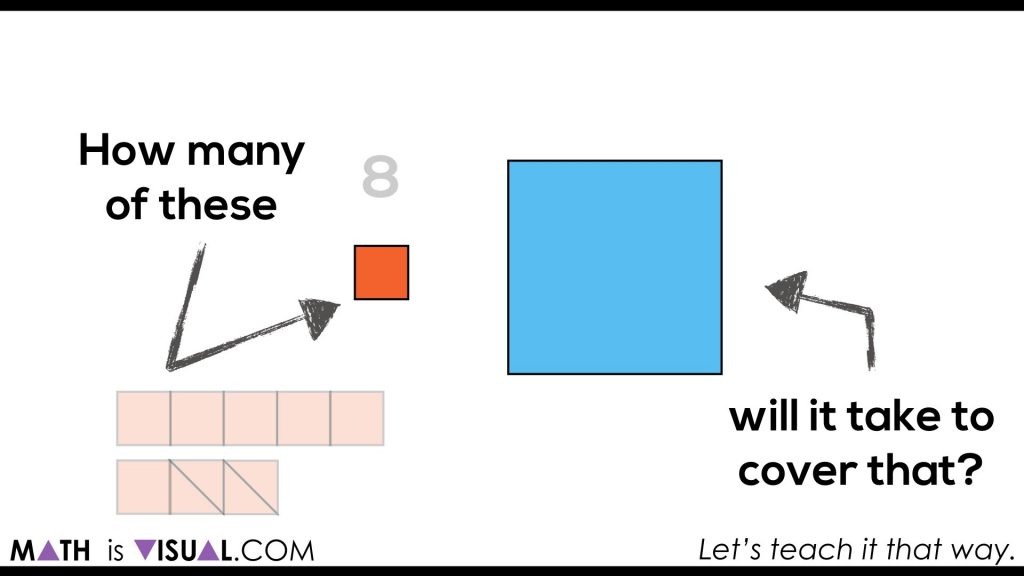
The video then shows that the number of squares doubles to go from the triangle, to the rectangle that was created with two of the original triangle. This is to build a visual understanding and intuition to help them get ready for deriving the formula for area of a triangle.

Visual Prompts – Set 2:

Let’s give them another go!

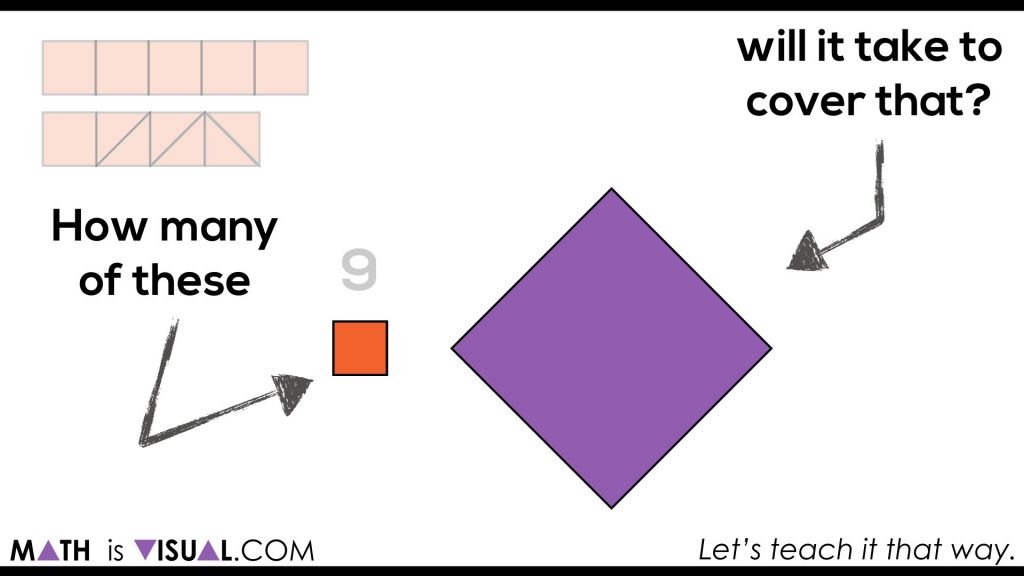
The Big Reveal:

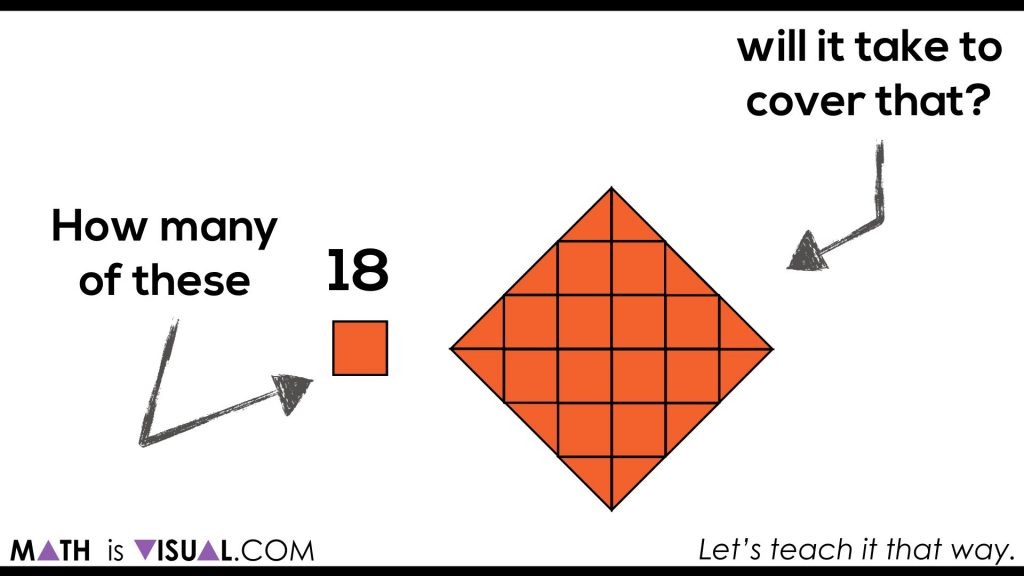
The video animates this and also counts out the squares as well.

Students are again challenged to determine how many squares it will take to cover a rectangle created with two triangles:

The video shows that you’ll need double the number of squares for the rectangle than for the triangle.

Visual Prompts – Set 3:

In the third set of visual prompts, we bring a grid onto the screen to start nudging students towards the doubling/halving relationship of triangles and rectangles as well as the strategy of taking the length times the width and dividing by 2.

Here’s where it begins:

Hopefully, some students in your class think about finding the area of the rectangle and then taking half:

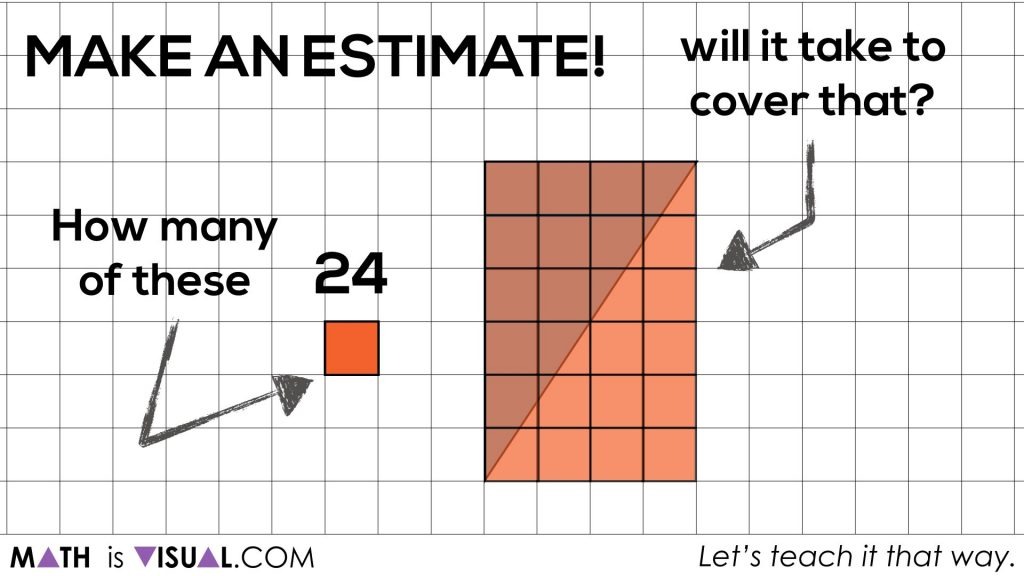
If students don’t go for that strategy, the visual prompts will help unpack this idea.

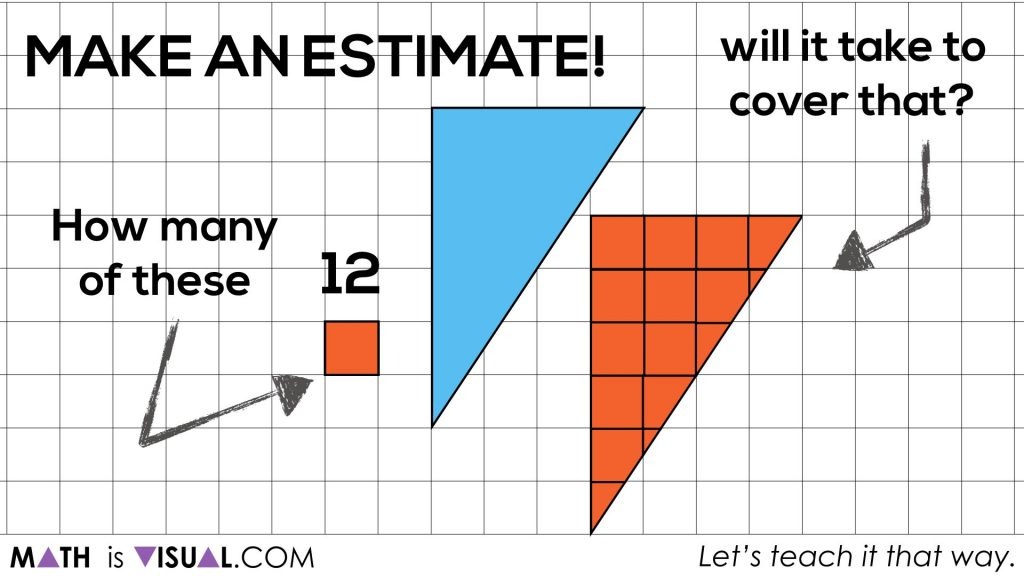
Just in case some students aren’t convinced that there are 12 whole squares on the screen, the video animates this to prove it visually:

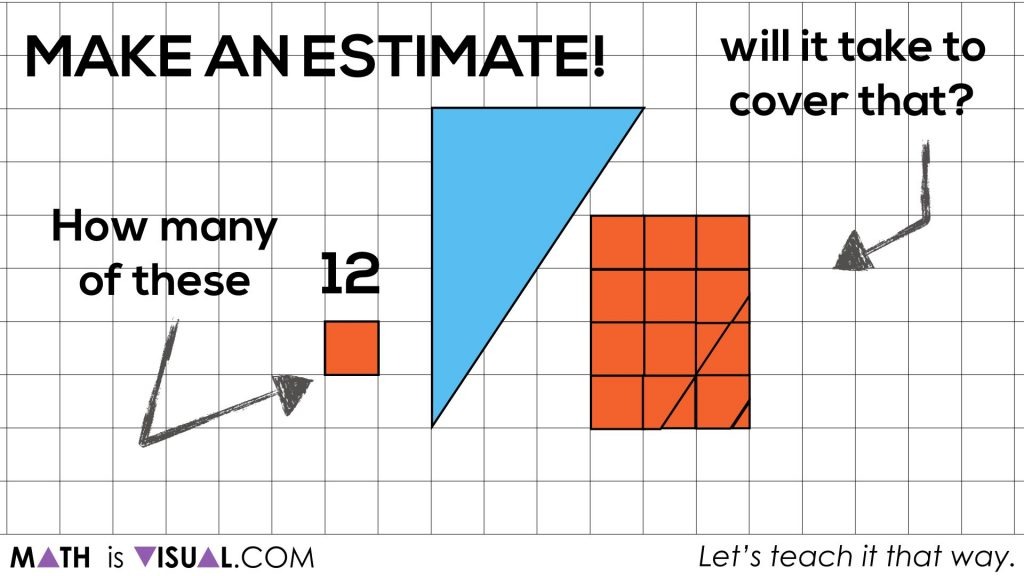
Again, for this set of visual prompts, we are trying to give students an opportunity to “play” with the area of a triangle without being pre-taught ahead of time. This is a simple inquiry-based way to introduce the idea using their prior knowledge, intuition and spatial reasoning.

From here, we can now start formalizing these student generated solutions to come up with the formula for the area of a triangle:

Area of a Triangle = Half of the Area of the Rectangle

or

A = Half of the Base x Height

or

A = (b x h) ÷ 2

Pretty awesome what mathematics can do when we approach it from a concrete and visual standpoint first to solidify our conceptual understanding before moving on to steps, procedures, and algorithms!

How’d It Go?

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.