Multiplication Number Talk – Unpacking Halving and Doubling Using Number Properties

Number Talks have become commonplace in many elementary math classrooms across North America to help students build their number sense and overall number fluency. This is amazing news! However, the reality is that while using number talks in the classroom can be helpful, I have witnessed on a number of occasions where students learn how to apply strategies without fully understanding why they work.

With the recent release of the new Ontario Ministry of Education Focusing on the Fundamentals of Math: A Teacher’s Guide document, I thought I’d pick something that is highlighted from the document and dive into it deeply from an approach outlined in the guide such as the Alex Lawson quote included in the document:

Children should learn their number facts. However, they would benefit from learning these facts by using an increasingly sophisticated series of strategies rather than by jumping directly to memorization.

Lawson, A. (2016, April). The mathematical territory between direct modelling and proficiency. What works? Research into Practice (64).

For Ontario teachers, it is worth noting that the “new” document is simply highlighting parts of the current Ontario Grade 1 to 8 Mathematics Curriculum and is not new content. It is also worth noting that in this document that was advertised to go “back to basics,” is really just highlighting parts of the curriculum that the Ministry considers “fundamentals”. However, please know that this document does not promote rote memorization without understanding. When you search for the word “basic,” you find it in the actual text only twice, while the word “understand” comes up 46 times. So while this document was pitched as a “back to basics” document stuffed full of demands for rote memorization without worrying about conceptual understanding, that isn’t true at all. It is very well balanced and I’m very proud to share it with teachers in my district and across the province of Ontario.

To support the work of this document, I’m attempting to build in a Jo Boaler-style visual number talk series of visual prompts for multiplication to unpack, through investigation, the halving and doubling strategy. This is a great way to lower the floor on this task and ensure that all students in your classroom have an entry point.

Keep an eye out for number properties as we will be unpacking those near the end. The silent solution video is much longer than usual because I attempt to fully unpack how the halving and doubling strategy works using number properties.

Let’s dive in!

Visual Prompt #1: Open Questioning to Lower the Floor

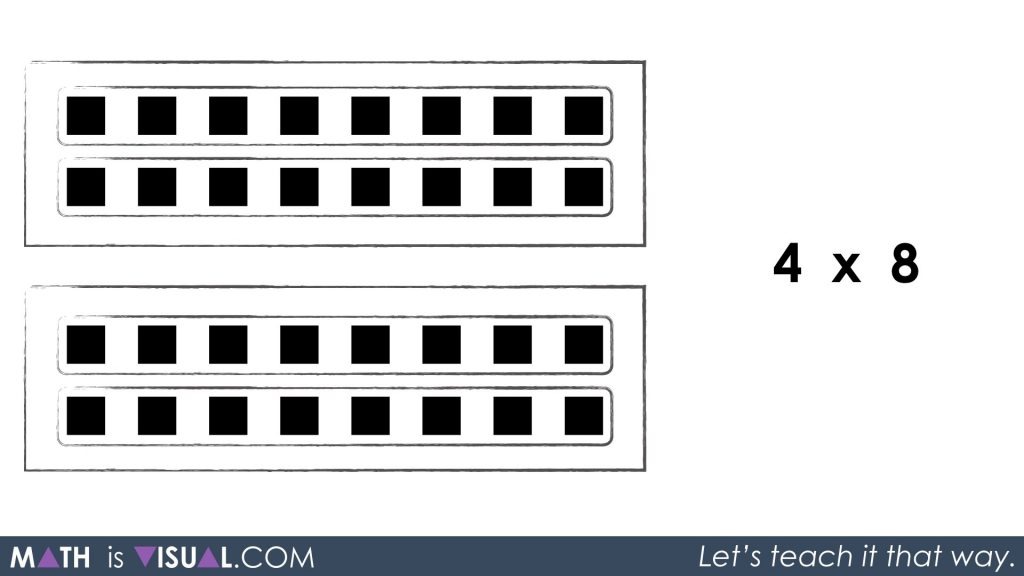
In the video above, we start with the following visual:

The prompt I would give students here is something like this:

Describe how many squares you see in as many ways as possible to your neighbour.

The intention here is for students to get beyond saying “32,” and to start saying things like:

• 4 groups of 8
• 8 groups of 4
• 4 plus 4 plus 4 plus 4 plus 4 plus 4 plus 4 plus 4
• 2 groups of 16
• …and so on

Then, I’d explicitly share this image:

By using the above image, I’d then prompt students with:

What might you say to describe how we have grouped the squares now?

Note that we are still leaving the questioning quite open, however I’m anticipating that students might say something like:

• 4 groups of 8; or,
• 8 items copied 4 times.

If I’m leading this visual number talk in a classroom, I’d be recording what students are saying on the chalkboard / whiteboard to model their description visually and symbolically.

Here’s what we might display for students who say “4 groups of 8” to ensure that all other students can “see” what the student sharing sees:

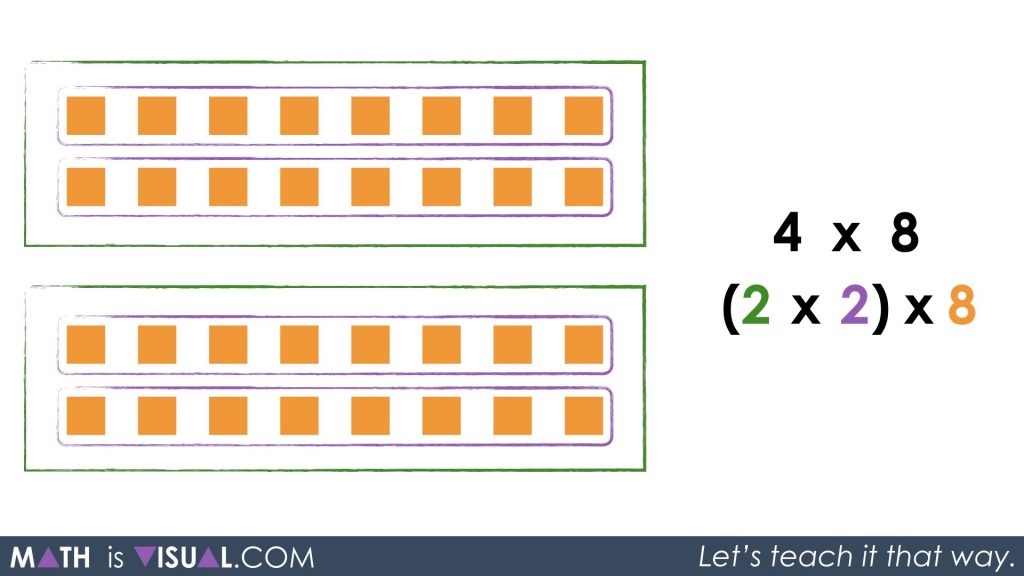
Then, I might display the same 32 squares, but re-group visually to show the following:

I’d then prompt students again to describe what they see and attempt to pay attention to the groupings outlined. Describe in words what it looks like and then, what could we write symbolically to represent the same groupings?

I am anticipating that students might come up with 2 groups of 2 groups of 8 or 2 groups of 8, copied 2 times, or similar.

The following visual shows what we might write to represent the verbal description of 2 groups of 2 groups of 8:

Although, another student might think of it more like this working from the inside out:

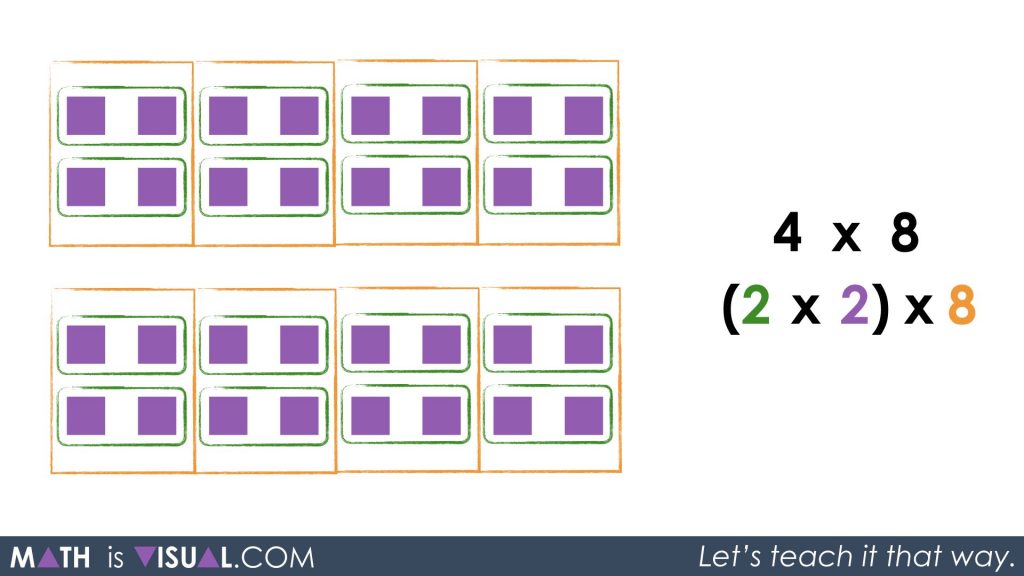
I would then re-group visually another time and ask students to share with a neighbour how they might describe the following:

Here, I’m anticipating hearing students say something like 2 groups of 8 groups of 2 items.

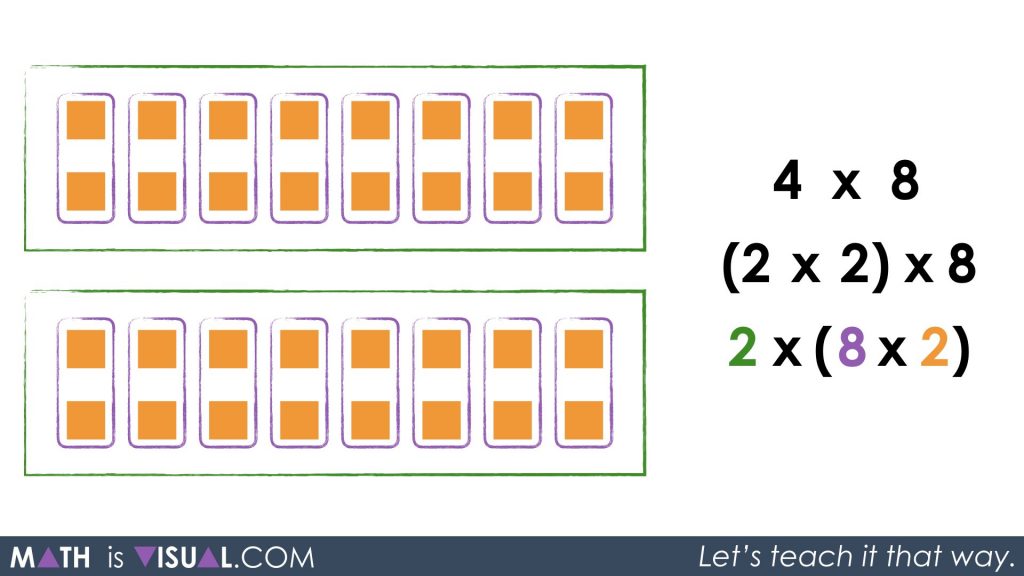
Again, we must keep in mind that other students might see it differently and we don’t want to discount how they are viewing things.

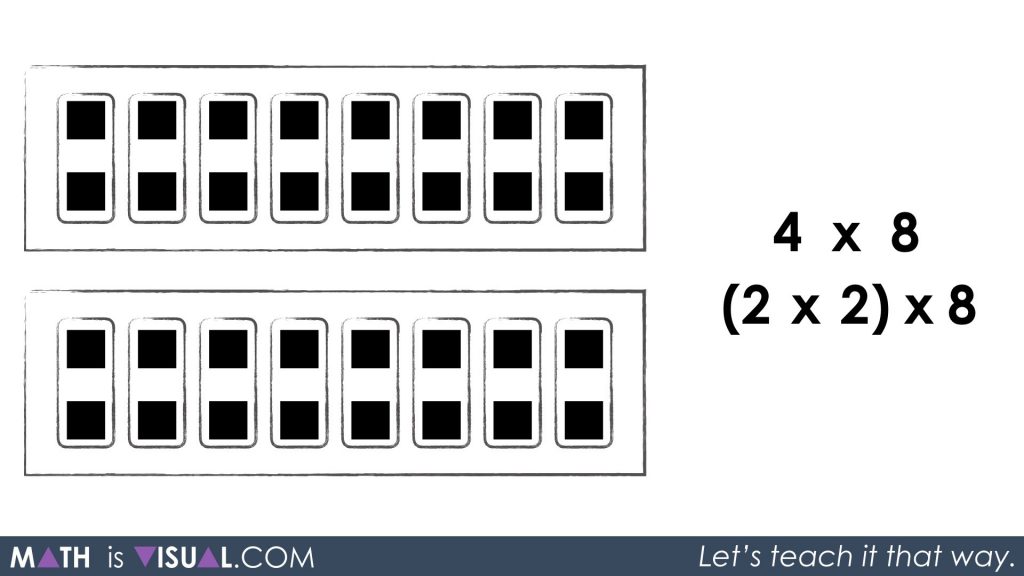
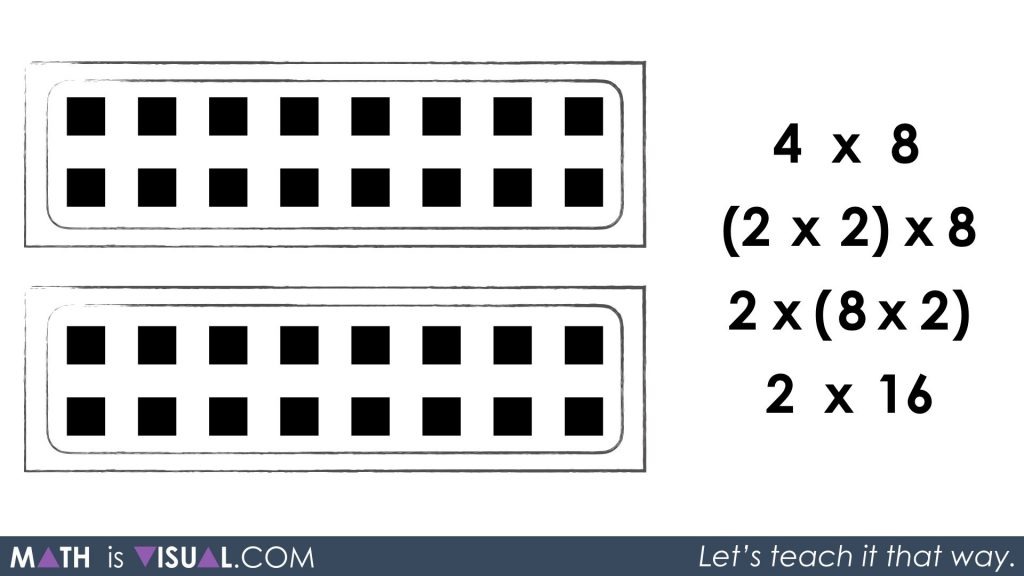
Re-grouping again to remove the groupings of 2 will result in the following:

Here, I’m anticipating students saying something like 2 groups of 16.

Then, I might re-group by simply placing each group of 16 into another group like shown below. What might students say now?

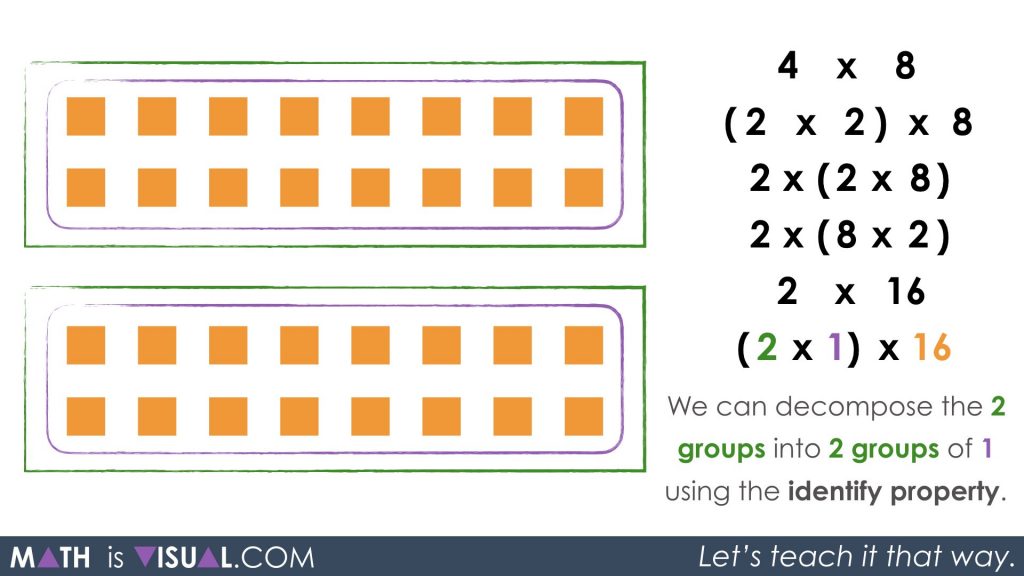
I’m anticipating that less students will see this right away, however what we have done is explicitly shared an example of the identity property:

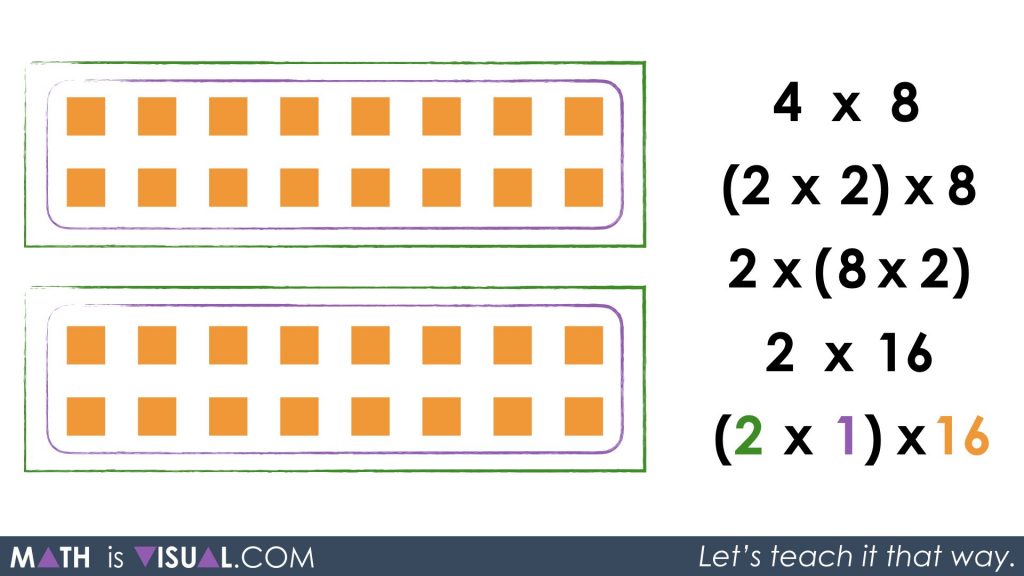
We basically have 2 groups of 1 group of 16. The identity property shows up when I place a single group inside another group. The result is the same, but it is something students must be able to understand very clearly. This is a way to help them play with this idea in a friendly manner.

If we re-group again, we can ask students how they’d describe the following:

I’m thinking that we might hear something like 1 group of 16 groups of 2 or similar.

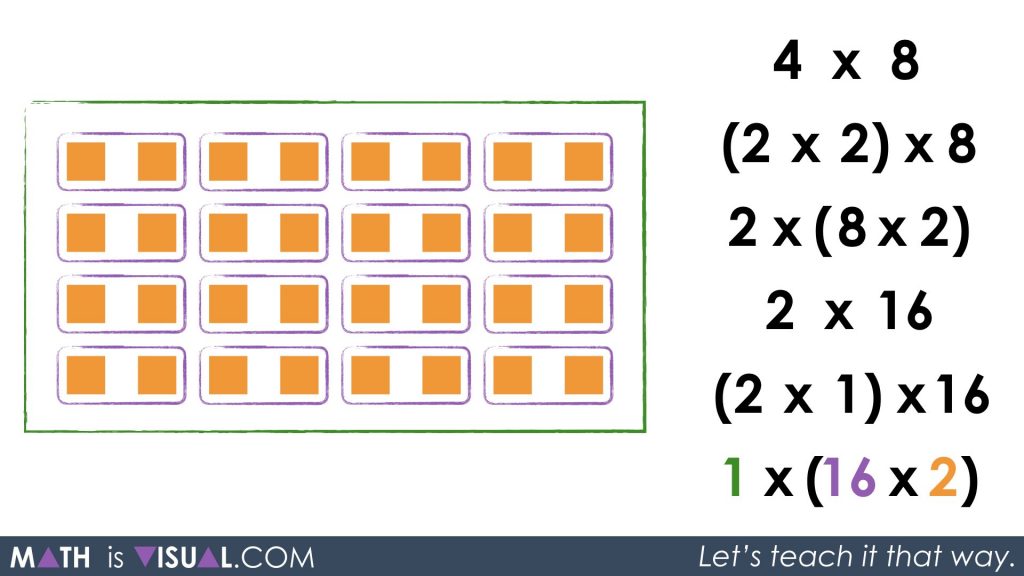
And then finally, 32 cubes total:

Wow, that was a lot of manipulating for something as seemingly simple as 4 x 8.

Something I mention to teachers when sharing out visual number talks like this is how many times students have not only had to wrestle with conceptual understanding, but also practice their math facts in order to come to the final answer. It’s like we’ve tricked them into practicing math facts, but built on the conceptual underpinnings!

DOUBLE-WHAMMY!

Unpacking What’s Really Happening Here

Number Properties “Under the Hood” of the Halving and Doubling Strategy

While it might not seem apparent initially, we have done a lot with number properties in order to be able to apply a halving and doubling strategy to this seemingly simple multiplication problem.

Let’s take a closer look.

In order to apply a halving and doubling or doubling and halving strategy, we must decompose the number to be halved into a half and double, in this case, decomposing 4 into factors of 2 and 2.

Right there lies the half and the double, or 2 groups of 2 groups of 8. Note that the factors of 2 and 2 are still associated with one another (hence the brackets around them):

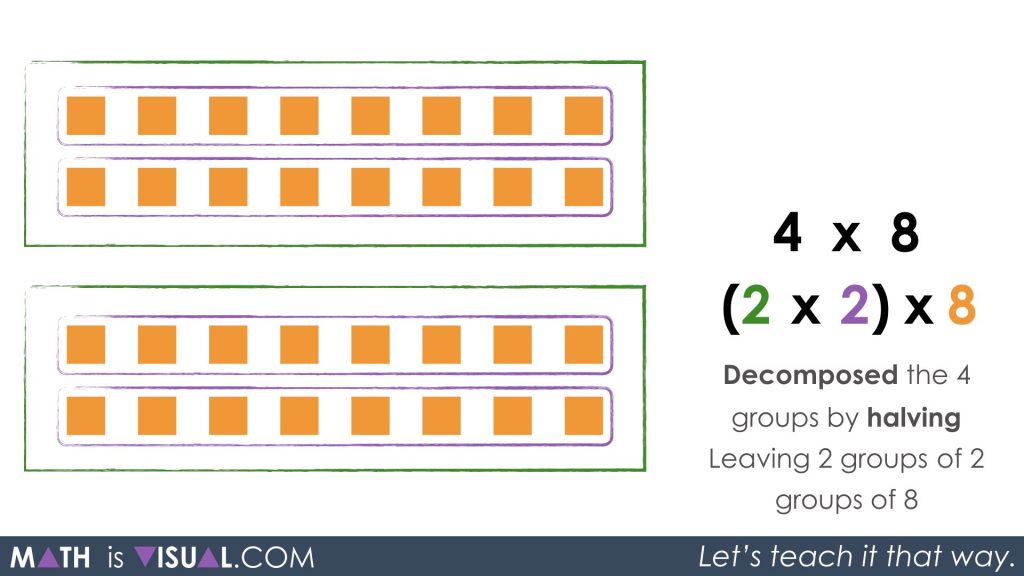
Since the intention here is to half the 4 and double the 8, we must re-associate a factor of 2 with the 8.

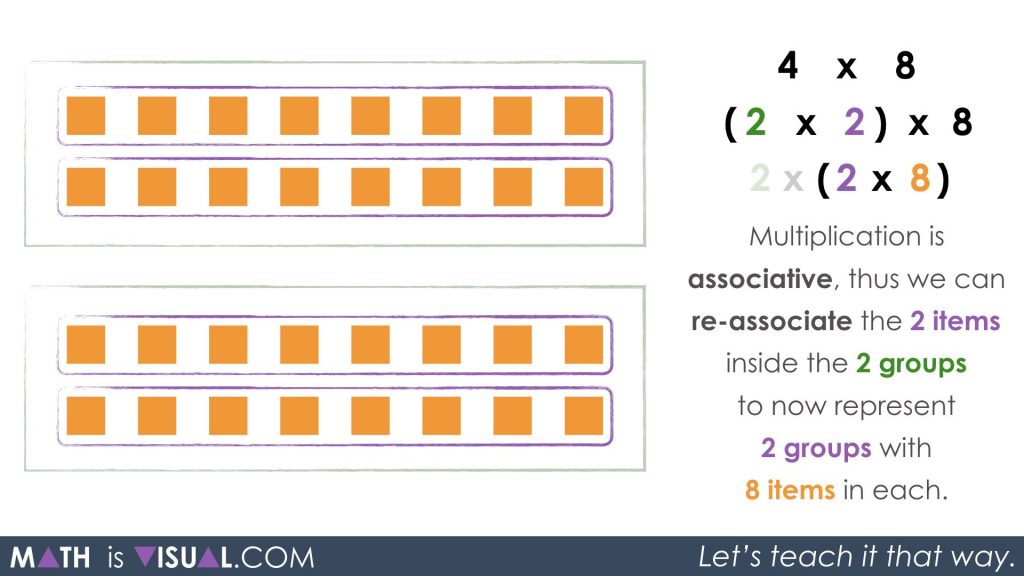
The result is 2 groups of 2 groups of 8 or 2 groups of 8, copied 2 times.

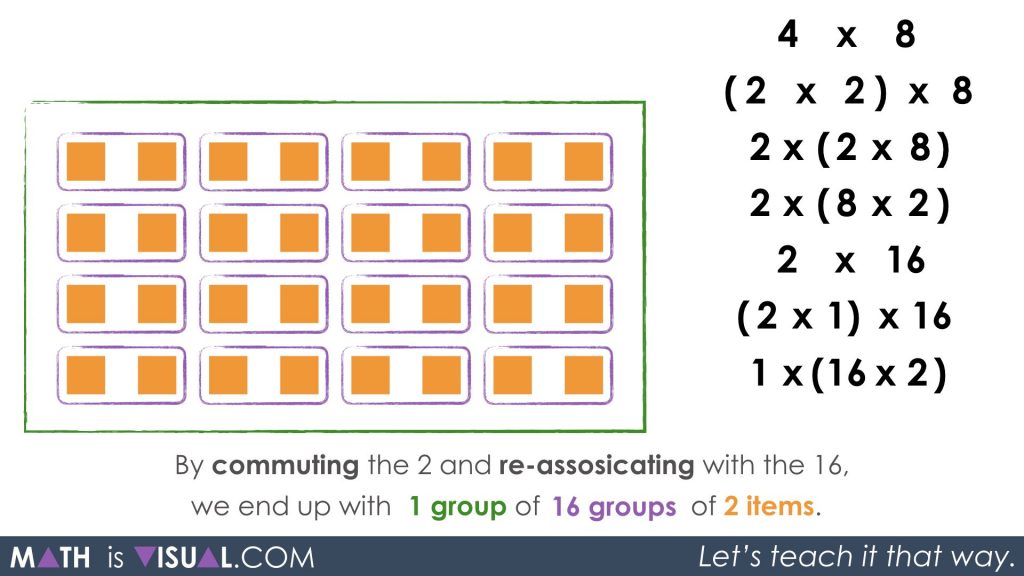
We could also commute the factors of 2 and 8 in order to regroup into what would visually appear to be 2 groups of 8 groups of 2 or 8 groups of 2, copied 2 times:

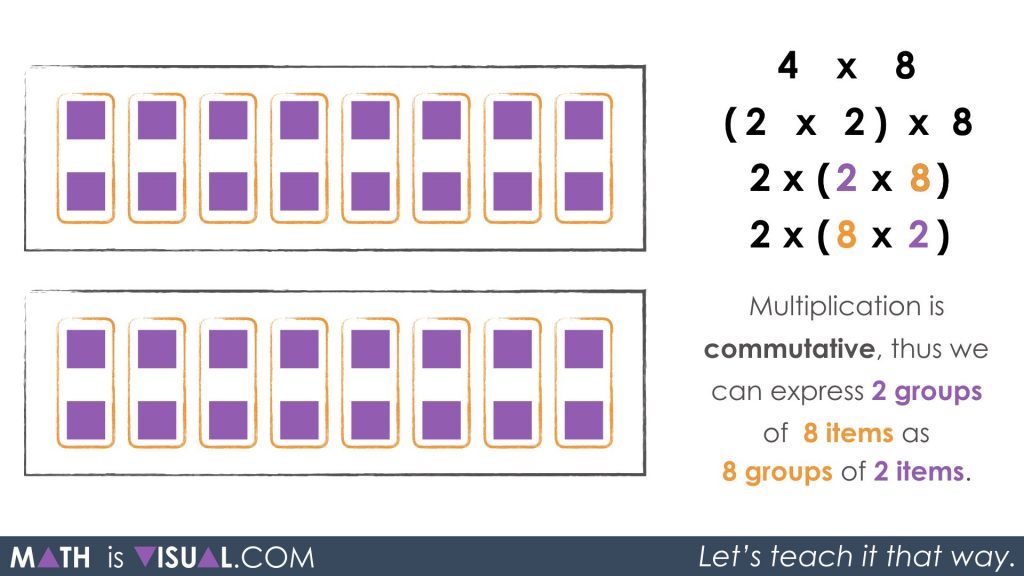
When you re-group the 8 groups of 2 through simplification to 16, we can now see 2 groups of 16:

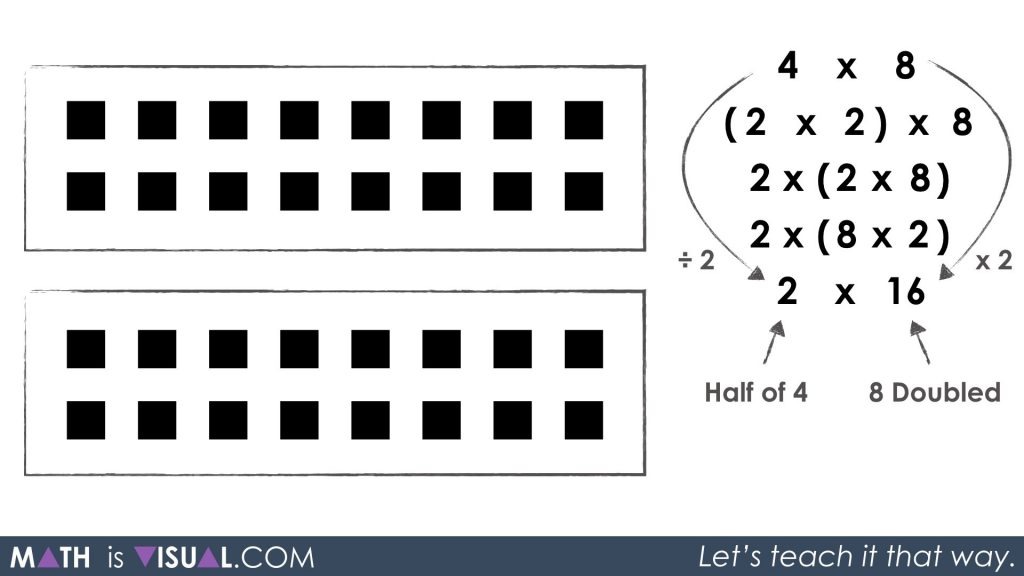
Here, we can clearly see the halving and doubling taking place.

While not necessary, you can explicitly see the identity property at play here by placing a single group inside another single group:

If you want to play around with more number properties, we can commute the factor of 2 and re-associate it with the factor of 16 using the commutative and associative properties:

And finally, by simplifying, our result would be 1 group of 32 or simply 32 squares total.

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.

Dive into conceptual math talks that are embedded in problem based math units for use with your students now!