Subtraction Using The Concrete Number Line

As you know from the variety of topics and grade bands covered on the Math Is Visual website, visualizing mathematics is really important; first concretely, then pictorially, and finally, symbolically. 

While I stress the importance of mathematical models for thinking and representing mathematics, it is common for educators to promote emerging certain mathematical models before students are developmentally ready. 

The same is true for the most commonly used linear model: the number line. 

Research cited by Cathy Fosnot in this video shows that “increasing reliance on linear representations of numbers plays a central role in the development of numerical knowledge” (Ramani & Siegler, 2008). While this is fantastic news and a great reason to be planning with linear models in mind, we also don’t want to jump straight to a number line with some of our youngest learners.

So, how can we help leverage linear models and help students pave their own pathways to number lines?

Well, let’s start with the number path like we did in a recent set of Math Is Visual prompts and connect this idea concretely to a number line by building concrete number lines.

In this series of Math Is Visual prompts, we will connect the ideas of number paths and concrete number lines using connecting cubes (or linking cubes).

We will first build a sense of magnitude between 1 and 10 and then engage in subtraction problems using the concrete number line to explore two types of subtraction: comparison subtraction and separating subtraction (also known as removal or take-away).

Remember that you can use any set of Math Is Visual prompts as lesson starters, math talks, number talks, or number routines in the classroom or at home with your kids!

As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and visually after consolidating in the classroom through student work.

Let’s get started…

Sparking Curiosity

Let’s take some time to Spark Curiosity using the Make Math Moments “Curiosity Path” as we always do.

In this case, we will start with a visual number path and explicitly connect it to a concrete number line using connecting cubes.

Then, we will press students for their understanding of magnitude with numbers from 1 to 10 by asking where are the 5th cube, 3rd cube, and 9th cube on the concrete number line.

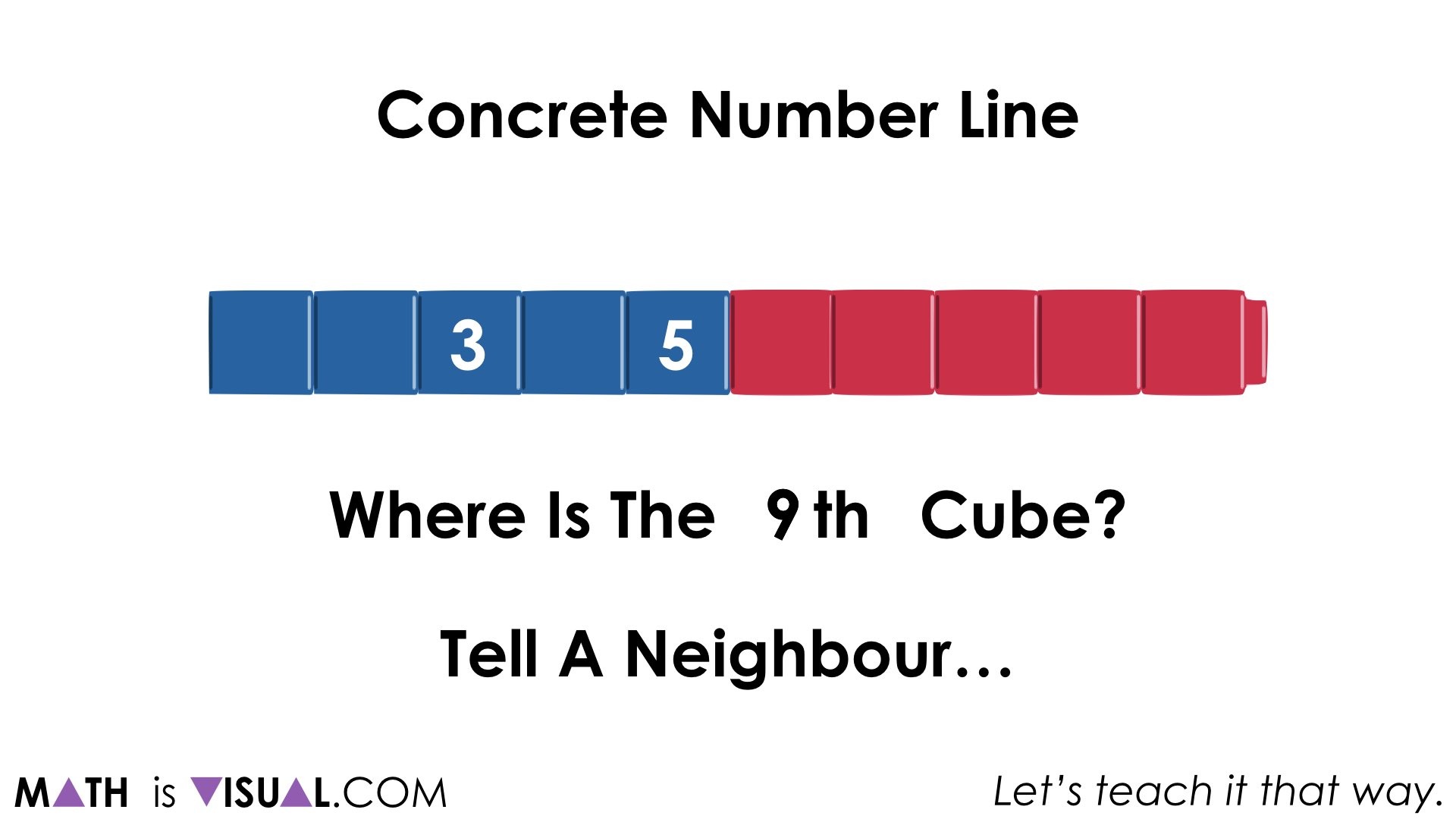
The visual prompts give time between each for students to think and describe to a neighbour.

Then, the question is posed:

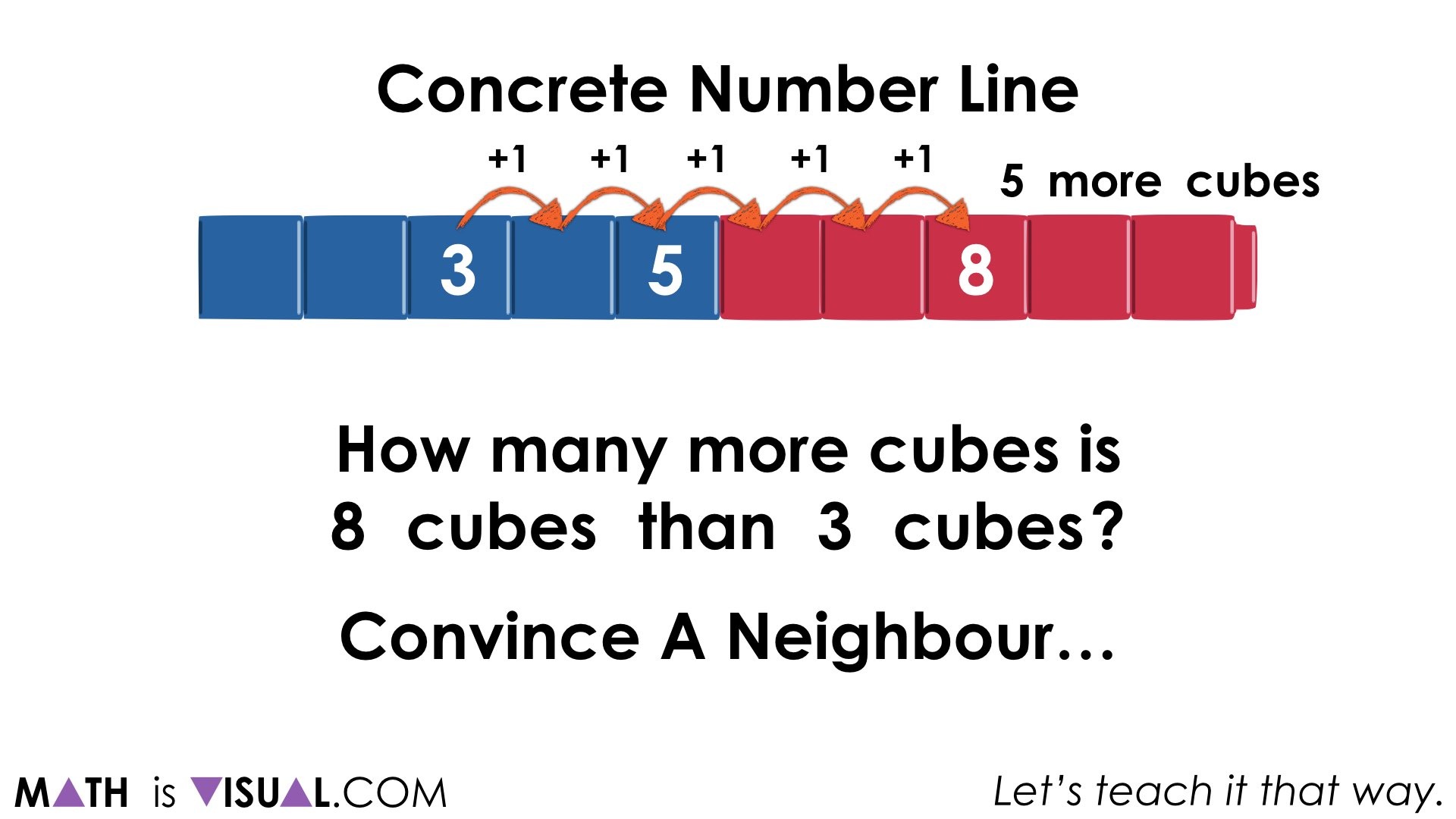
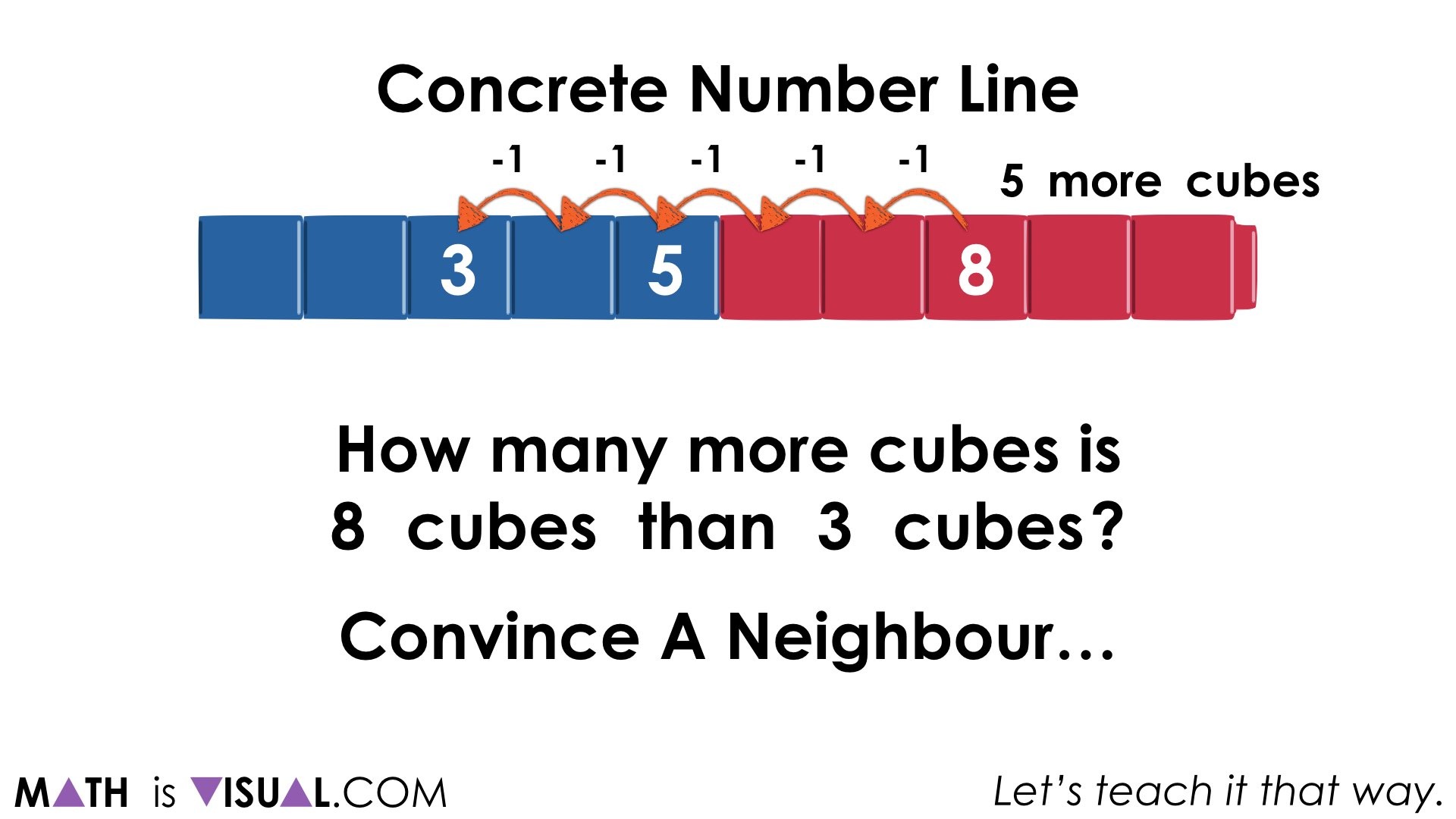
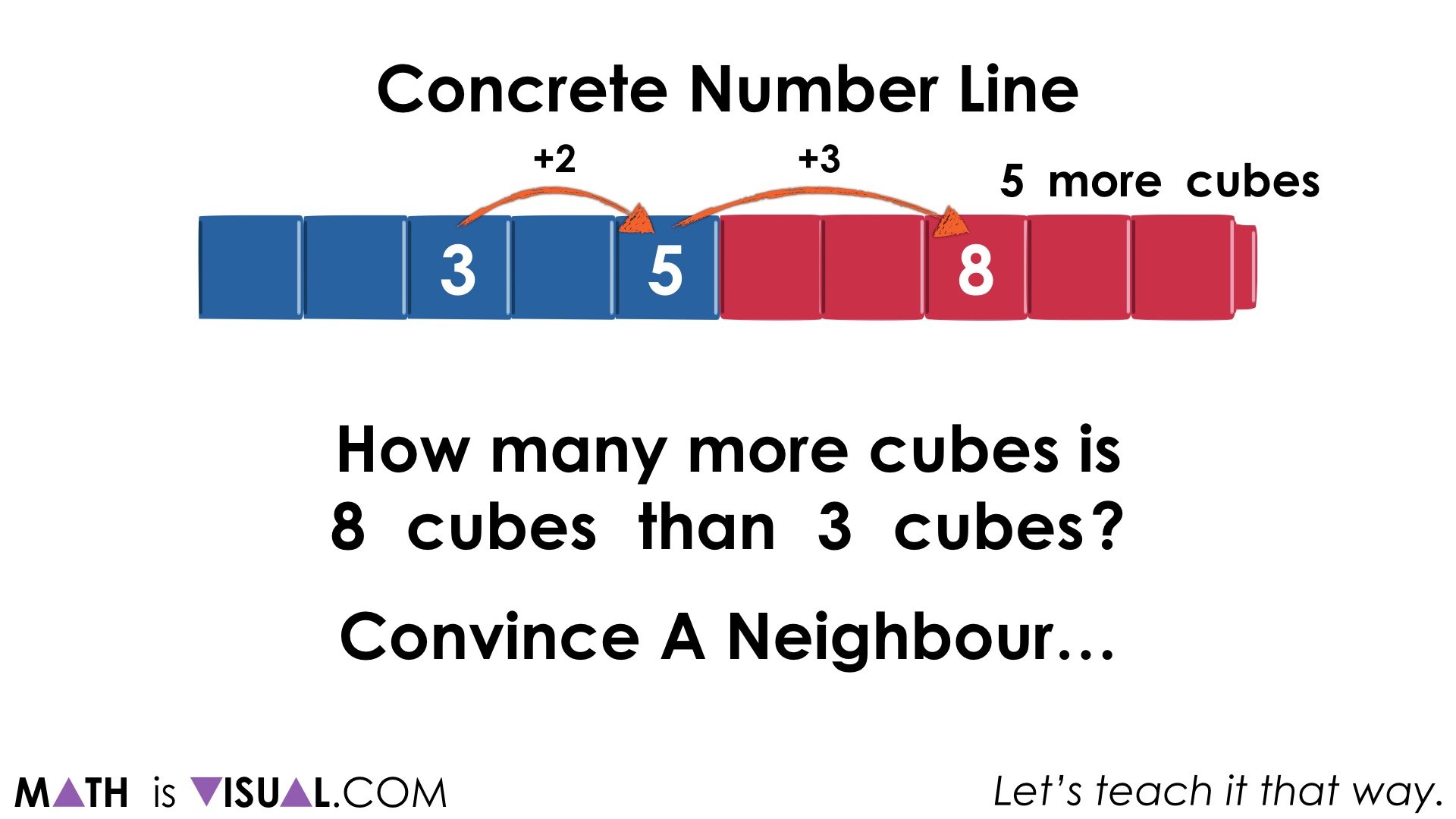
How many more cubes is 8 cubes than 3 cubes?

Pause where the visual prompt video indicates and give students some time to convince their neighbours.

I’d recommend annotating student thinking using a concrete model.

You can use magnetic connecting cubes / linking cubes on a black/whiteboard or even tape them up and use chalk or marker to annotate to the best of your ability. Your goal is to try and show student thinking utilizing the connecting cubes concrete number line. 

Some possible strategies include:

…counting on from 3 by 1’s (one-to-one):

… starting at 8 and counting back by 1’s to 3:

…making a jump forward by 2, then 3 starting at 3 or making jumps of 3 then 2 backward from 8:

… some students might make one big jump of 5 forward or backward starting at 3 or 8, respectively:

Then, give students a similar problem using the same values of 8 and 3, but with a different context:

Lui has 8 cubes. 

He gives 3 cubes to Bella.

How many cubes does Lui have leftover?

Pause the visual prompts where indicated and give students time to think and then convince their neighbours.

When students share their strategies, you might notice that fewer strategies emerge with this context or some strategies may not match this particular context. 

Here are a couple you might see:

… making 3 jumps of 1 cube starting from 8:

… making 1 jump of 3 cubes backward starting at 8:

We’ll now ask students what they notice and what they wonder about these two problems, side by side on the screen. Be sure to pause the visual prompt video to give them some thinking time before turning and talking.

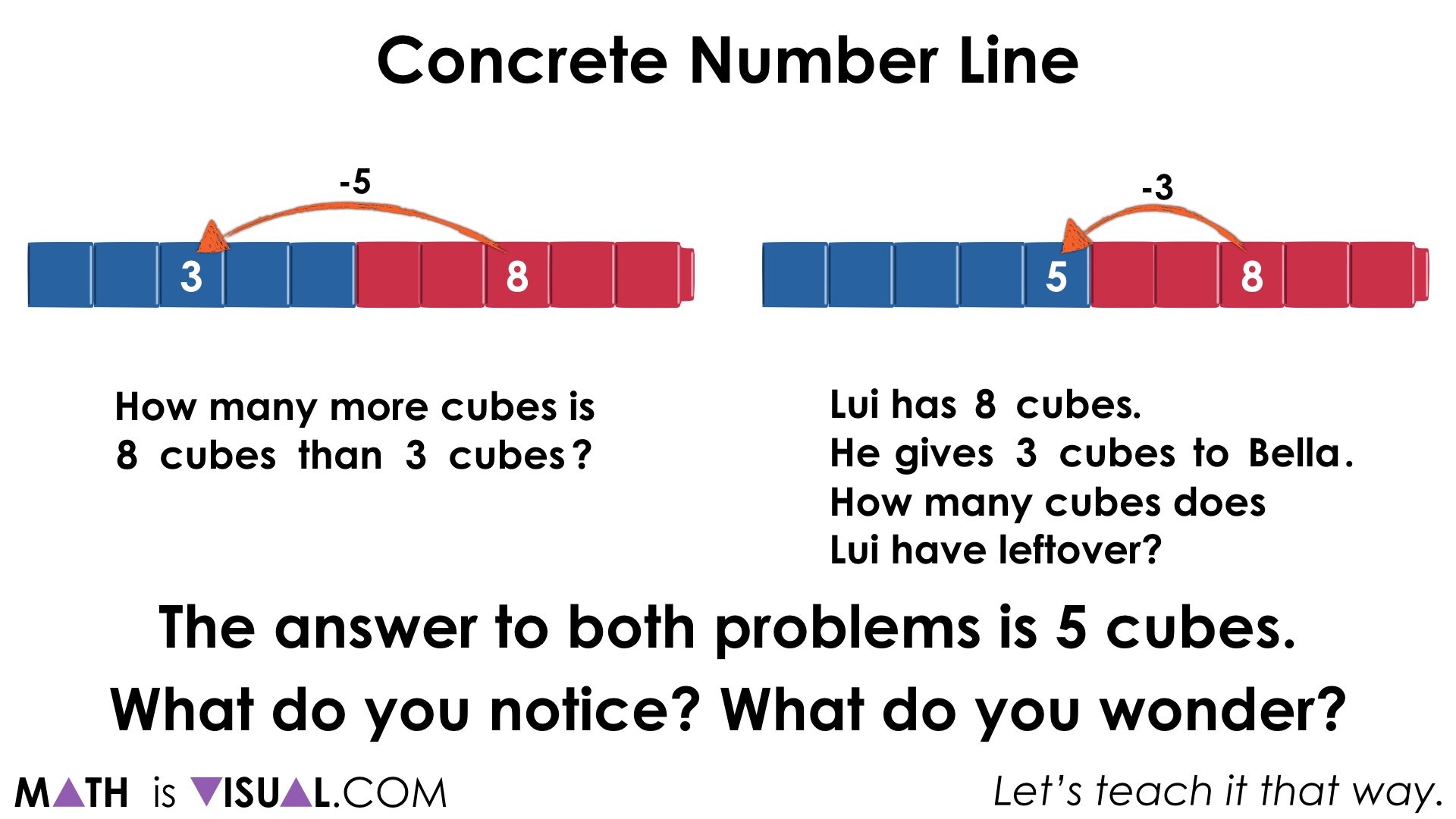
Some students might notice that while the “answer” to both problems is 5 cubes, how each problem was modelled is different.

It actually looks different.

I wonder why that is?

Some students might notice that in one case (on the left) we jumped forward or backward by a total of 5 cubes, whereas the other case (on the right) we jumped back by 3 cubes.

They may not notice initially, but we also couldn’t jump forward by 3 in the case on the right.  I wonder why that is?

Some students might notice that on the left, we are comparing how much bigger 8 is than 3 whereas on the right, we are taking away 3 cubes. 

I might ask my students what operation is taking place in the left and what operation is taking place on the right.

Will they know that they are both subtraction problems, but different types of subtraction?

After students have had time to discuss their noticings and wonderings, it is time to consolidate the learning.

On the left, we have a comparison subtraction context while on the right we have a separating subtraction (also known as removal or take away subtraction).

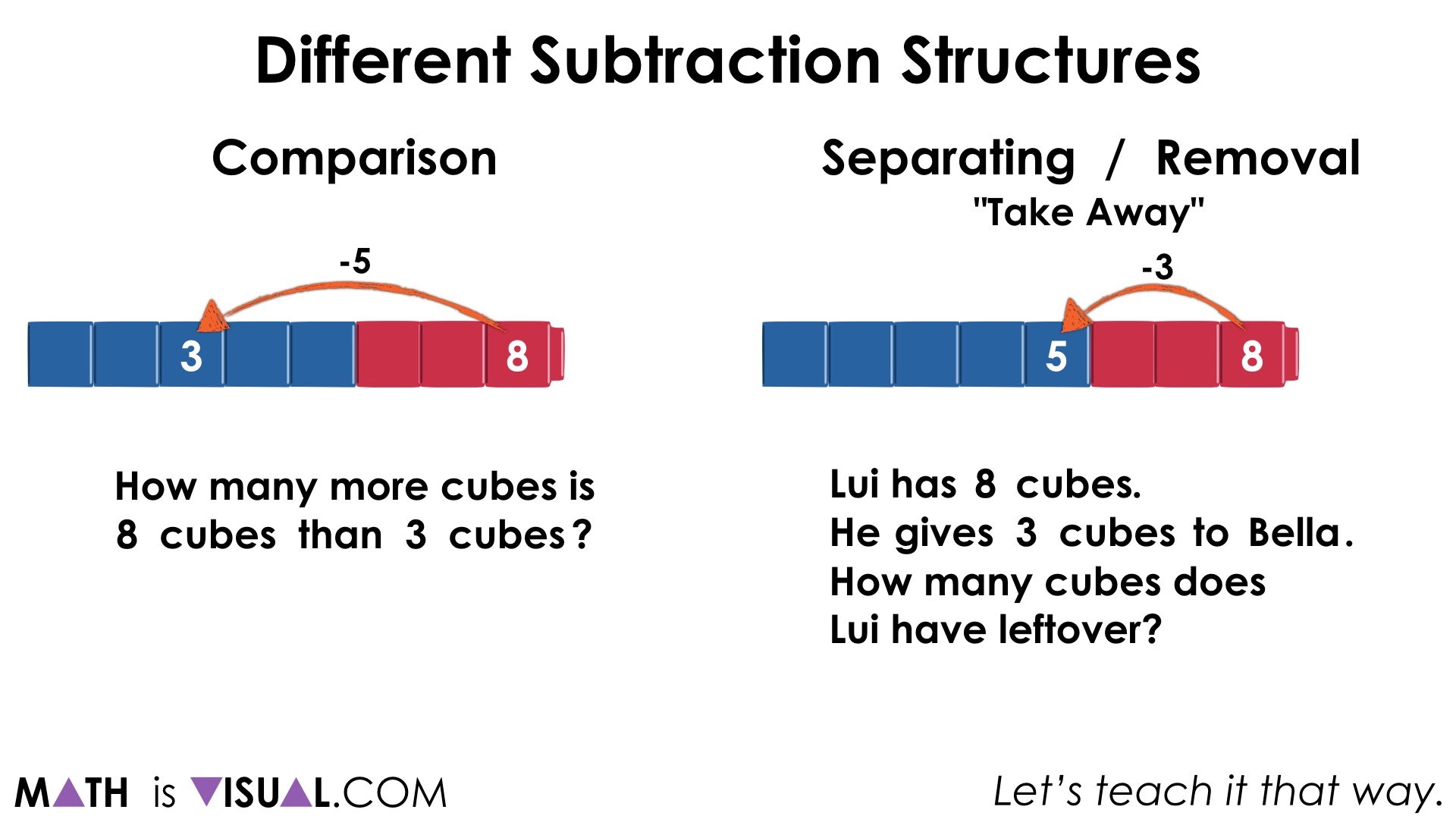
Interestingly enough, it is common for educators to teach students early on that subtraction means take away, when in reality, it only means take away some of the time; particularly when the context involves separating a quantity or removing a part from the whole. 

Contexts involving a comparison of two quantities and determining how many more or less one quantity is than the other (or the difference) looks very different than separating / removal / take away: 

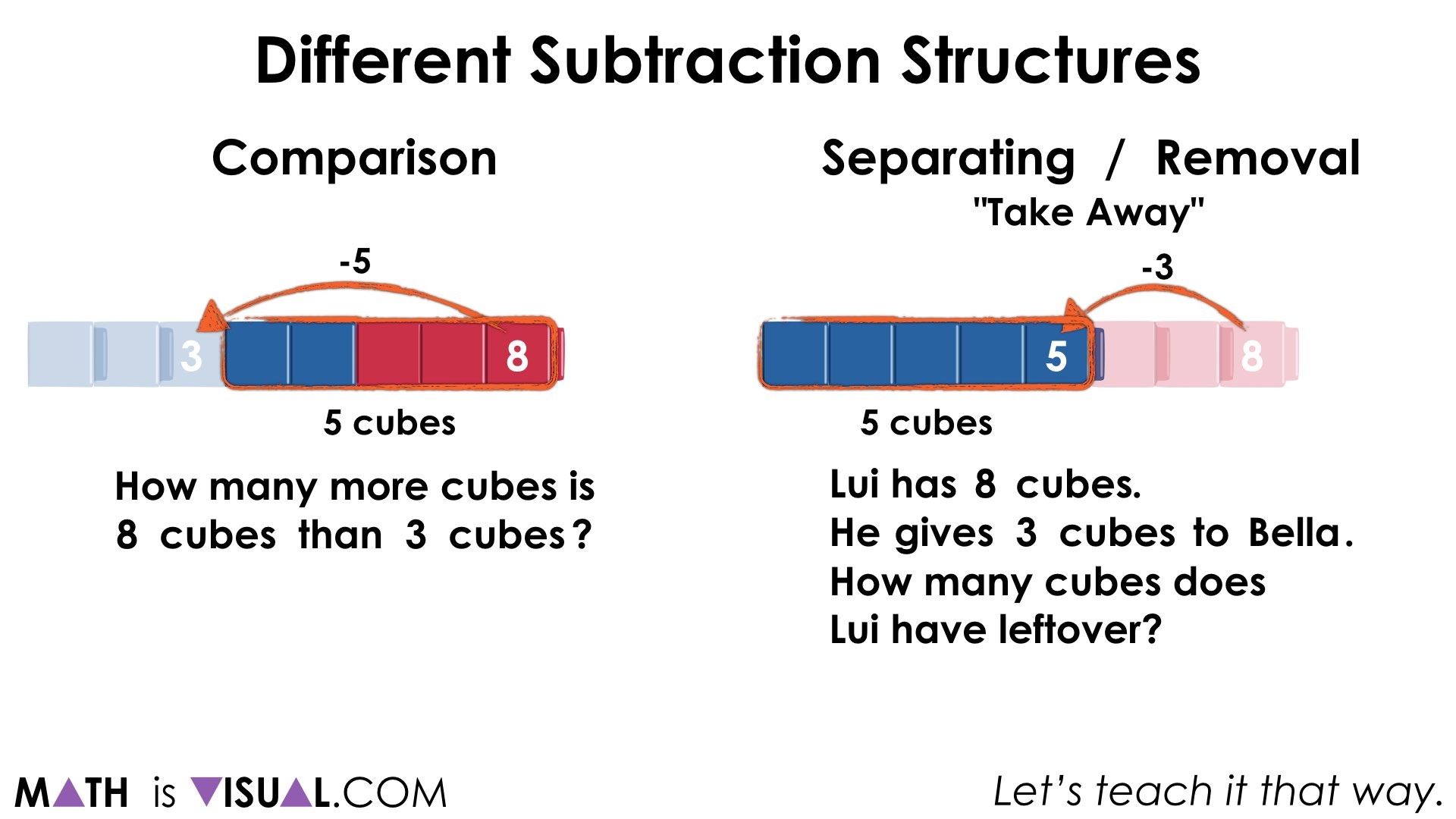
You may notice that in the comparison situation, the difference is found in the jump, where as in the separating situation, we see the subtrahend as the jump and the difference is the remaining cubes.

When was the first time that you realized subtraction wasn’t just take-aways?

It’s ok.

This is new learning for me, too!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.

Be sure to dive into our real world math lessons that Spark Curiosity and Fuel Sense Making through the use of visuals.