After the previous post on visualizing whole number quotative and partitive division, we are now ready to start tackling integer division. If you have not yet viewed the visual animation and visual prompts for whole number division, you definitely should before moving on.
The next three posts will focus on integer division to finish off the integer operation series. In this video, we will address the division of a negative dividend by a negative divisor first using quotative (or measured) division, then partitive (or fair share) division. The viewer will also be prompted to pause the video and try one their own using concrete manipualtives and/or visuals.
See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.
Visual Prompt #1: Quotative Division
In the video above, we start with dividing a negative by a negative through quotative division:
-8 ÷ (-2) = ___
in words:
-8 divided into groups of -2 gives a result of ___ groups
So, let’s have the viewer model concretely and/or visually the following:

Students may use spatial reasoning to create groups of a set or linearly on a number line. They may also consider using repeated subtraction to repeatedly take away groups of -2 until all are removed (or 0 remain).
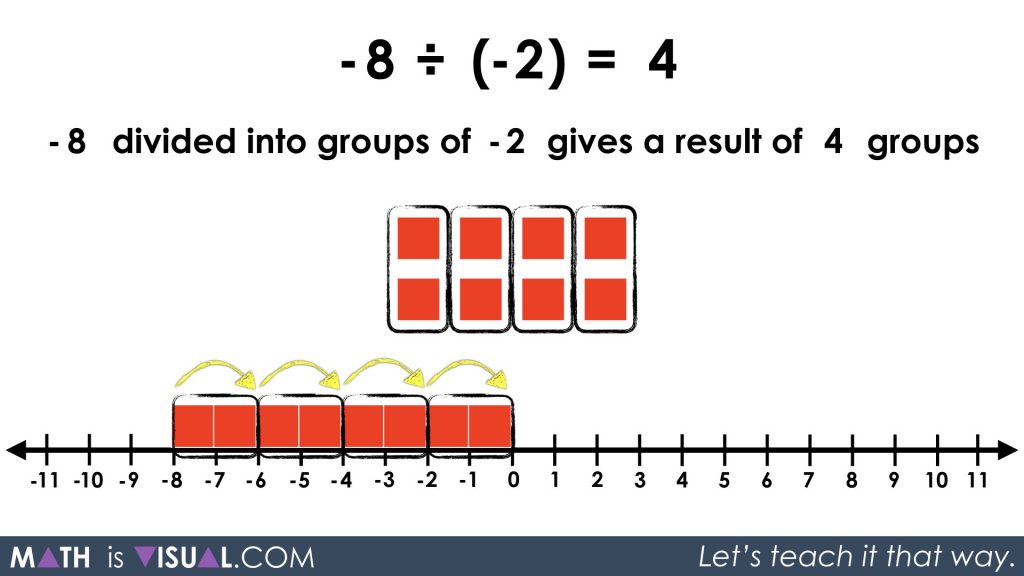
The arrow can also be pointing to the left if students use repeated addition to repeatedly add groups of -2 from 0 until they reach -8.
Visual Prompt #2: Partitive Division
Now we move on to approaching the same problem from a partitive division perspective:
-8 ÷ (-2) = ____
or
-8 divided into -2 groups gives a result of ____ per group.

Although the value of the result will be the same, the conceptual understanding and concrete/visual approach will look very different.
Similar to above, we can approach this using a set or linear model where we are spatially splitting the quantity into 2 equal, but “negatively charged” groups (since it is -2 groups) and counting the number of objects in each group. While the visual below may look awfully similar, note that the use of repeated subtraction might be a bit different because we do not know how many are in each group (yet). So, the repeated subtraction may consist of fair sharing 1 object at a time or 2 objects at a time, up to a quantity that a student is comfortable to subitize quickly for sharing out.
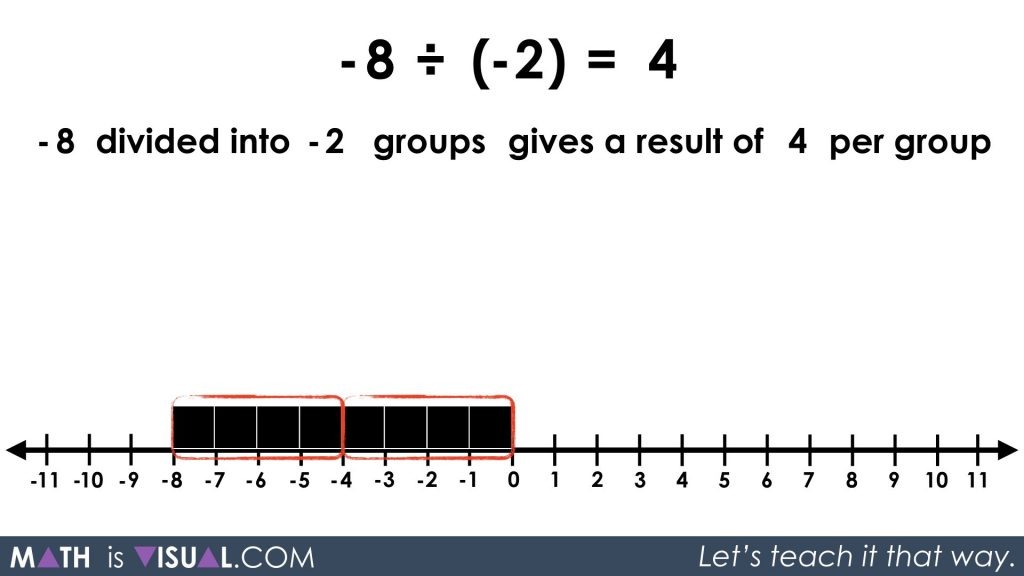
Since we are dividing the -8 into 2 negatively charged groups (groups of -2), then when we put each negative square into the negative group, we get a double-negative. This is very similar to when we use a double-negative in the English language. For example, if it is not going to not rain, then we get the positive – it’s going to rain!
In this case, the negatively charged group “negates” the negative values and thus we get positive values within the negatively charged group.
Visual Prompt #3: Your Turn!
Pause the video and let the viewer apply their knowledge of negative by a negative partitive division using the following visual prompt:
-10 ÷ (-5) = ___
or
-10 divided into -5 groups gives a result of ___ per group

Allow time for the viewer to engage in the partitive division before showing the remainder of the video animation or the following still image.
Again, we must note that we want to determine the value of the quantity that will be shared amongst 5 negatively charged groups.
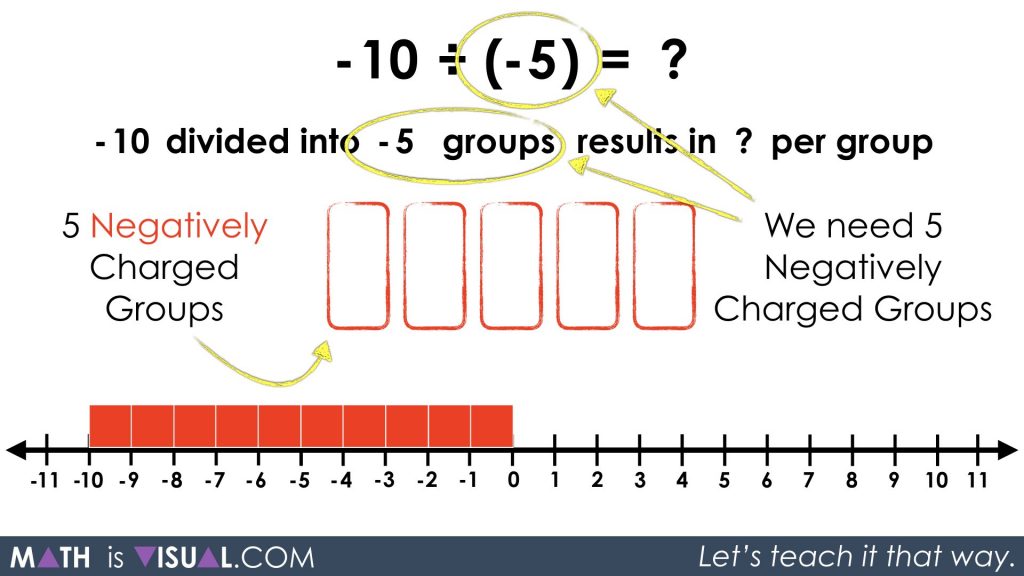
Thus, when we fair share the -10 into these 5 negatively charged groups (-5 groups), we will end up with +2 in each group:
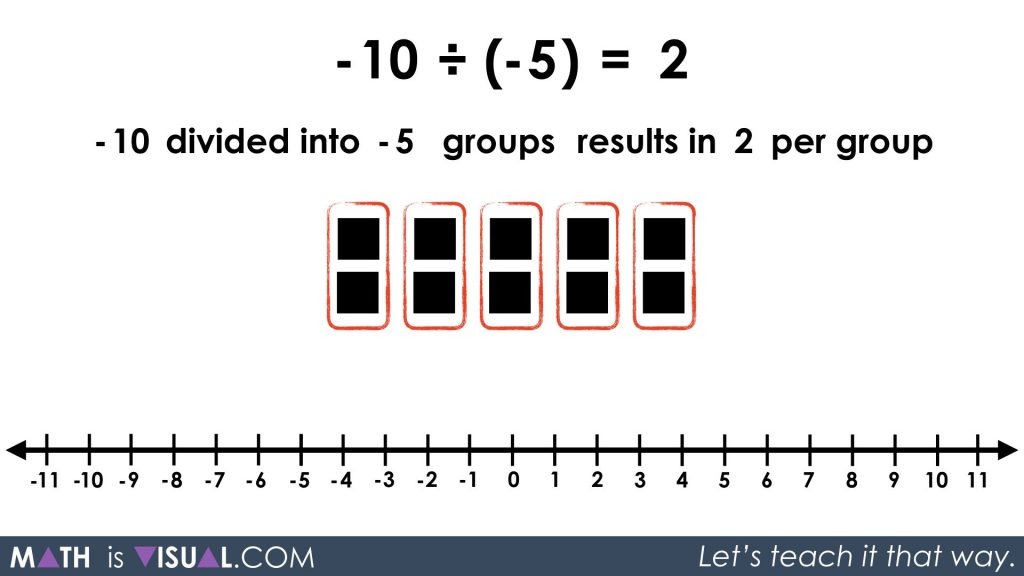
So, now you’re rocking with quotative and partitive division as well as division of a negative by a negative.
Are you ready to tackle dividing a negative by a positive and a positive by a negative?
They’re coming up in the next two posts, so get ready for them!
Math IS Visual. Let’s teach it that way.



In the video of a negative divided by a negative it seems like you have black squares and red boxes representing negative divided by negative and resulting in positive. Shouldn’t they both be red?
Hi Laura!
I think you might be referencing this part:
This is a tricky one because we’ve taken 10 negative ‘squares’ and divided them by 5 negative groups… when the “negative” squares “enter” the negative groups, it results in the opposite sign.