In This Set of Math Visual Prompts…
Students will explore modelling and solving two-step algebraic equations involving multiplication and division.
Intentionality…
This set of visual math talk prompts is taken from the Math Talk section of Day 5 in the Make Math Moments Problem Based Unit called Planting Flowers Revisited. The purpose of the Math Talk is to reinforce key concepts and big ideas from this problem based math unit including:
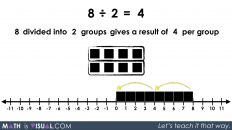
- There are two types of division;
- Quotative division is when the total quota is known (the dividend), and the number per group or the rate (the divisor) is known;
- Quotative division reveals the number of copies or iterations of a rate that can be derived from the overall quota (the dividend);
- In quotative division, the dividend and the divisor have the same unit;
- Partitive division is when the total quota is known (the dividend), and the number of parts or groups (the divisor) is known;
- Partitive division reveals a rate;
- In partitive division, the dividend and the divisor often have different units;
- The dividend from any division sentence can be decomposed into smaller parts to allow for friendlier division by the divisor. This strategy is known as partial quotients. (i.e.: 85 ÷ 5 = 45 ÷ 5 + 40 ÷ 5 = 9 + 8 = 17);
- Division is the inverse operation of multiplication;
- Subtraction is the inverse operation of addition;
- Variables are used to represent changing or unknown quantities;
- When solving an equation where the coefficient of the unknown variable is not equal to 1, division is required to determine the value of the unknown variable and the context of the problem determines which type of division is required.
- A two-step equation is an algebraic equation that takes you two steps to solve.
Unsure about some of the terminology listed above?
Learn more about multiplicative thinking, rates, ratios and the roadmap to proportional relationships through the course: The Concept Holding Your Students Back.
Preparing to Facilitate
In today’s math talk, students will use an appropriate model to solve the following one-step algebraic equations eliciting both partitive and quotative division. Encourage students to name the type of division required to solve and to create a context for each equation. Students are encouraged to use a model to solve and/or communicate their thinking.
m(8) + 7 = 39
7(p) – 8 = 34
Two (2) additional visual math prompts are shared in the Teacher Guide from Day 5 of the Planting Flowers Revisited problem based math unit.
Although you could lead this math talk by orally sharing the context and representing student thinking on a chalkboard/whiteboard, consider leveraging the following visual math talk prompt videos to ensure accessibility for all students. We would recommend that you still model student thinking to ensure student voice is honoured prior to sharing the visual silent solution shared in the visual prompt video.
Visual Math Talk Prompt #1
Begin playing the video to share the first visual math talk prompt and be ready to pause the video for think time.
In the video, students are presented with visuals and a text prompt to set the context involving rows of poppies (a type of plant) and daffodils (another type of plant). The context might sound something like this:
Rows of 8 poppies are planted in the garden.
An additional 7 daffodils are planted nearby.
There are 39 plants in total.
How many rows of poppies are there?
Write an equation and solve.
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 01 - MATH TALK Visual Prompt Image 001](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-01-MATH-TALK-Visual-Prompt-Image-001-1024x576.jpeg)
The equation we hope students land on is:
m(8) + 7 = 39
Note that we have used a non-traditional format for this equation because we are trying to be intentional about m representing the number of groups or rows of poppies to help students realize that this means we are dealing with a quotative division situation.
Before we can get to dividing quotatively, we must first take care of the extra daffodil plants that have increased the quantity to 39 plants in total.
We can do this by subtracting the 7 daffodils on both sides of the equation.
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 01 - MATH TALK Visual Prompt Image 002](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-01-MATH-TALK-Visual-Prompt-Image-002-1024x576.jpeg)
This leaves us with 32 poppy plants and a rate of 8 poppy plants per row. From here, we can leverage quotative division to determine the number of rows of poppy plants there must be.
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 01 - MATH TALK Visual Prompt Image 003](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-01-MATH-TALK-Visual-Prompt-Image-003-1-1024x576.jpeg)
Although you must do your best to model student thinking and honour their voice, ask the student if you can show their thinking on a linear model or ask them if they can “see” their thinking on the double number line to promote the use of this powerful model.
Visual Math Talk Prompt #2
Continue playing the video until prompted to pause.
The context outlined in the video sounds something like this:
7 rows of poppies are planted in the garden.
After removing 8 of the poppy plants, a total of 34 plants remain.
How many poppies are there in each row?
Write an equation and solve.
The equation we are hoping students will land on is:
7(p) – 8 = 34
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 02 - MATH TALK Visual Prompt Image 001](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-02-MATH-TALK-Visual-Prompt-Image-001-1-1024x576.jpeg)
As we explored in the 2nd math talk prompt, we are in a situation where we hope to reveal the rate per row. This means that we will be leveraging partitive division once we account for the 8 poppy plants that were removed.
Since 8 poppy plants were removed, we must add them back in order to determine the total number of plants when all rows are full.
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 02 - MATH TALK Visual Prompt Image 002](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-02-MATH-TALK-Visual-Prompt-Image-002-1024x576.jpeg)
Since we know there are 7 rows of poppy plants with a total of 42 poppy plants in total, we can use partitive division to determine the rate (i.e.: the number of poppy plants per row).
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 02 - MATH TALK Visual Prompt Image 003](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-02-MATH-TALK-Visual-Prompt-Image-003-1024x576.jpeg)
It can be helpful to help students visualize what happened symbolically, visually using the double number line and even more concretely using visuals to outline each row of poppys.
![Planting Flowers - Revisited [Day 5] - Purposeful Practice - 02 - MATH TALK Visual Prompt Image 004](https://mathisvisual.com/wp-content/uploads/2021/09/Planting-Flowers-Revisited-Day-5-Purposeful-Practice-02-MATH-TALK-Visual-Prompt-Image-004-1024x576.jpeg)
Again, Ensure that you This means the type of division we will be using in the last step of solving this two-step equation will be partitive since we are dividing to reveal the rate.
Want to Explore These Concepts & Skills Further?
Four (4) additional math talk prompts are available in Day 5 of the Planting Flowers Revisited problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.



Add comment