Solving Two-Step Equations Visually

In this series of Math Is Visual Prompts, students are given the opportunity to start solving two-step equations with partitive division through the use of cups to hide “squares” or connecting cubes where the cups are acting as the “parts” or “groups” in partitive division.

Need more support with partitive division? Consider diving into these resources:

• A full partitive and quotative division problem based unit
• Lessons using both types of division with larger whole numbers
• Partitive Division of Fractions 3 Act Math Task unit

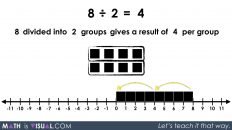
We also do our best to model this using the linear model of a number path (precursor to the number line) as well as abstractly using numbers and symbols.

As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and after consolidating in the classroom through student work.

Let’s get started…

Sparking Curiosity: Conceptual Subitizing Number Talk

First, we introduce this series of visual prompts with a really low floor by showing these squares before quickly covering them up:  

Covered up:

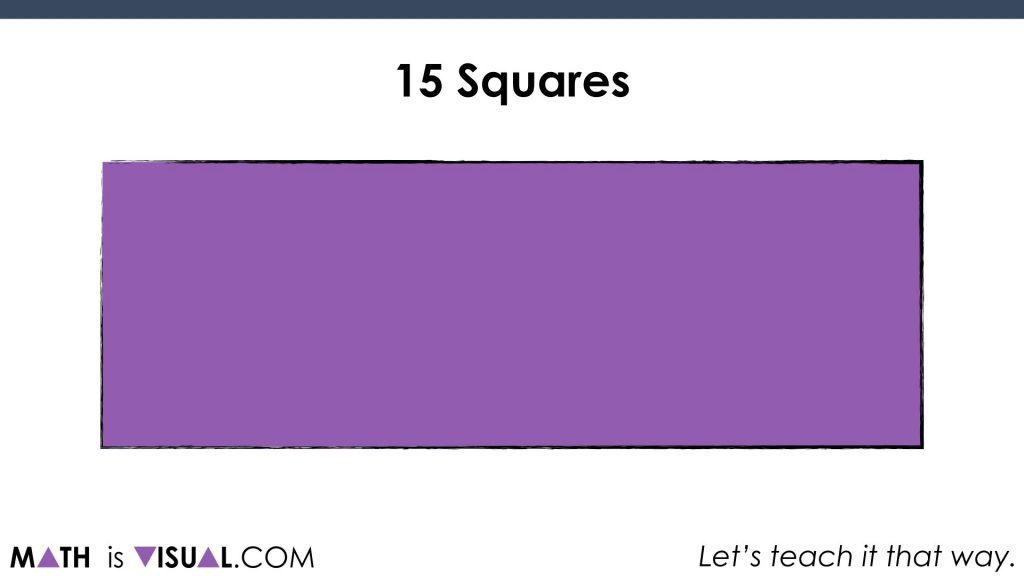
Students are then tasked with convincing their partners of how many squares they observed and how they know.

Then, we “slide in” a couple of red solo cups and reveal:

The question now becomes:

How many are under each cup if the squares were divided (partitively) amongst the cups evenly?

When you actually provide the concrete manipulatives for students to use, this is a pretty easy activity and all students can access this task. 

When you ask students, everyone will say “4”, which is great!

However, we want to make sure that they are clearly articulating what is happening here. 

Something students (and teachers) can easily miss is that this is a specific type of division known as partitive division. 

Want to learn more about partitive and quotative division? Check out my post on tapintoteenminds.com about the progression of division here.

Challenge #2: Another Partitive Division Scenario

Here we go:

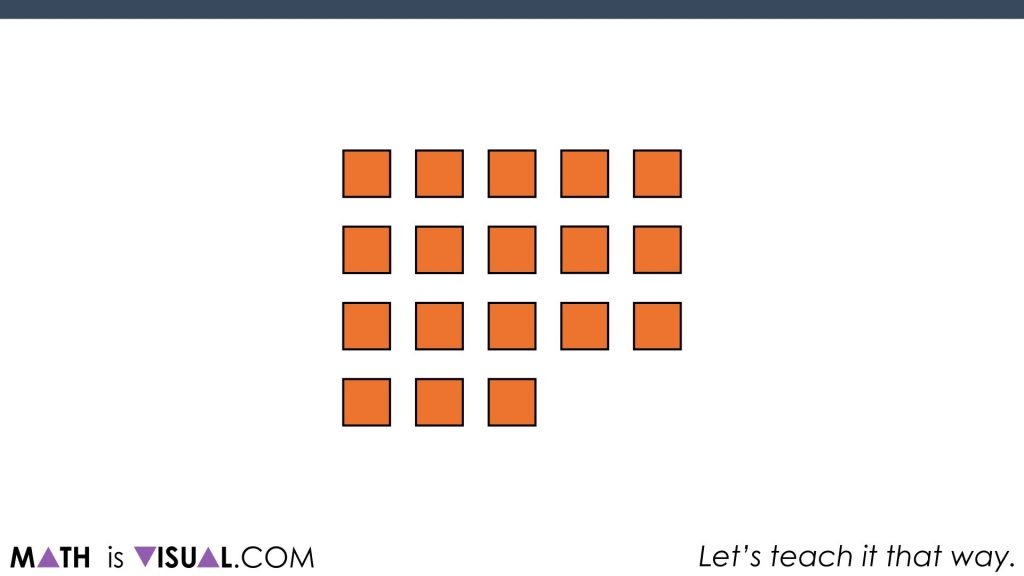
Students are then asked to determine how many squares before we cover them up and to say how they “saw” the squares.

Then, they are tasked to determine how many squares are under each of the cups now:

With the use of manipulatives or mental math strategies, students will be able to come up with “7” as the result:

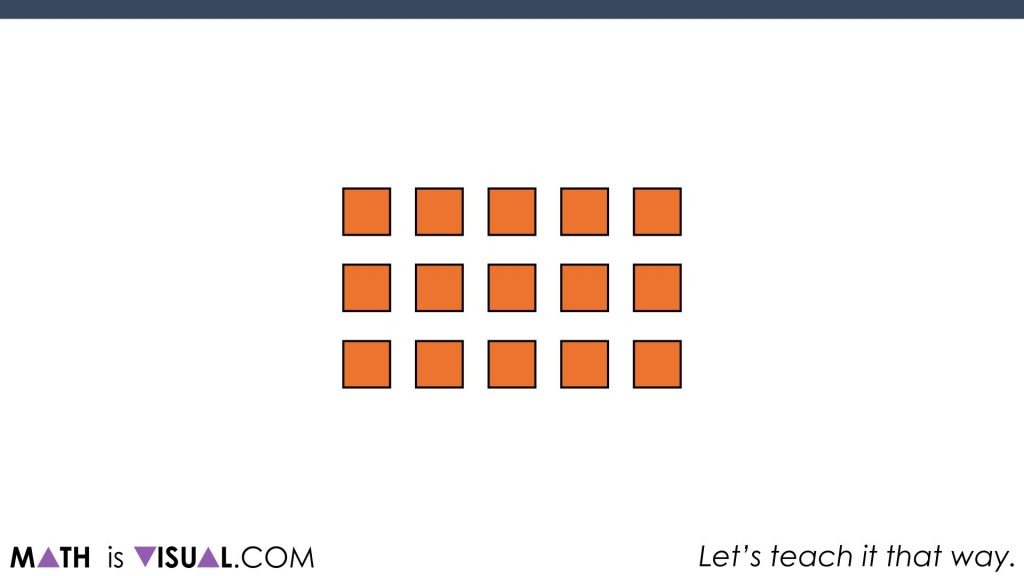
Challenge #3: 

Here’s the last challenge:

Again, students will be able to come up with “6” as the result:

Now, let’s tie this to a linear model using a number path (or concrete number line using connecting cubes):

This becomes pretty intuitive when we see it this way.

Now, let’s connect it to algebra:

Be sure to check out the visual prompts video at the top of the post to get the FULL EFFECT including “pause bars” to allow you to pause the video and let kids have think / discussion time.

How’d It Go?

Thanks for watching and reading!

Did you use this in your classroom or at home? How’d it go? Post in the comments!

If you’re looking to explore further, check out this problem based unit with a focus on evaluating expressions and solving equations.

Math IS Visual. Let’s teach it that way.

Be sure to dive into our real world math problems that Spark Curiosity and Fuel Sense Making through the use of visuals.