Visualizing Integer Division: Negative Divided By a Positive

May 23, 2018

7,557 views

5 min read

In this Math Is Visual video animation and visual prompts, we will explore integer division through quotative division and partitive division! In particular, we will explore a negative divided by a positive conceptually through concrete and visual representations!

So far in the integer division series, we have tackled the following ideas:

If you have yet to view those two posts, you should definitely go back prior to moving on to ensure that you are ready to grasp our next step in the Division of Integers Series: Negative Divided By a Positive.

This video and the next will focus on integer division with mixed signs to finish off the integer operation series. In this video, we will address the division of a negative dividend by a positive divisor first using partitive (or fair share) division, then quotative (or measured) division. The viewer will also be prompted to pause the video and try one their own using concrete manipualtives and/or visuals.

See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.

Visual Prompt #1: Partitive Division

In the video above, we start with dividing a negative by a negative through partitive division:

-8 ÷ 2 = ___

in words:

-8 divided into 2 groups gives a result of ___ per group

So, let’s have the viewer model concretely and/or visually the following:

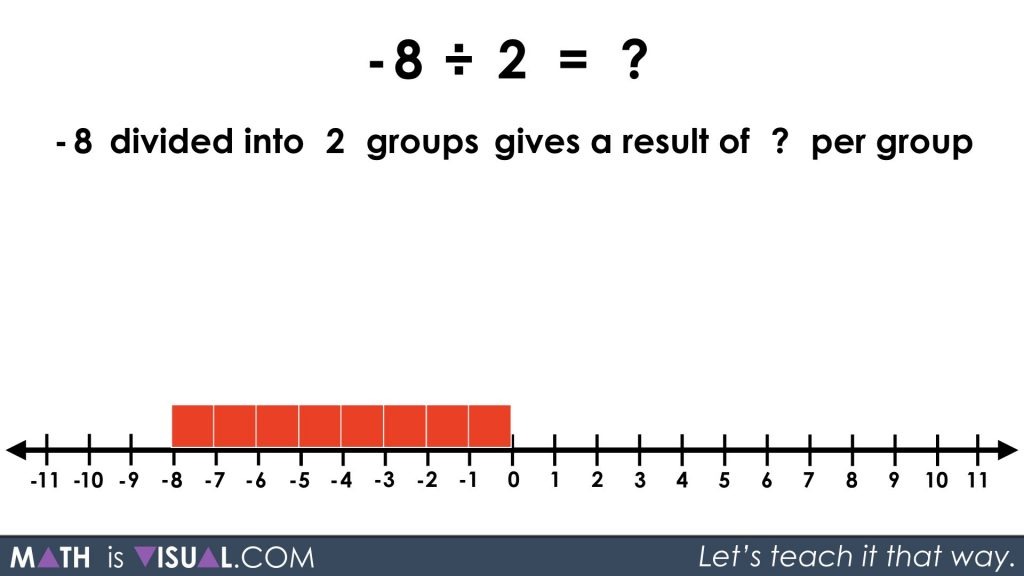
Integer Division - Negative Divided by Positive partitive -8 divided into 2 groups prompt

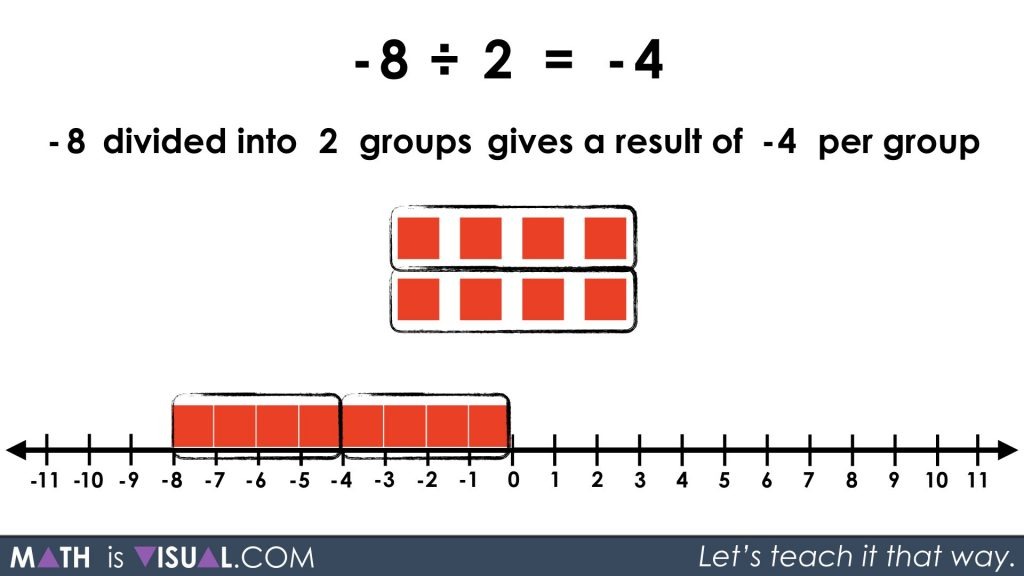
We can approach this using a set or linear model where we are spatially splitting the quantity into 2 equal groups and counting the number of objects in each group. We can think of this as repeated subtraction if we were to fair share 1 object at a time or 2 objects at a time, up to a quantity that a student is comfortable to subitize quickly for distributing equally to the two groups.

Integer Division - Negative Divided by Positive. partitive -8 divided into 2 groups prompt solution

Visual Prompt #2: Quotative Division

Now we move on to approaching the same problem from a partitive division perspective:

-8 ÷ 2 = ____

or

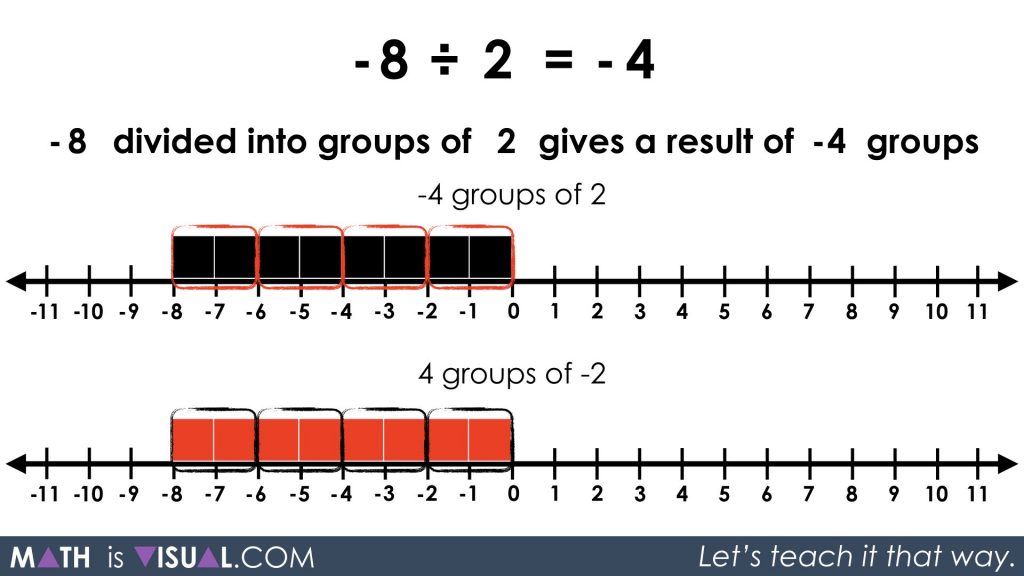
-8 divided into groups of 2 gives a result of ____ groups.

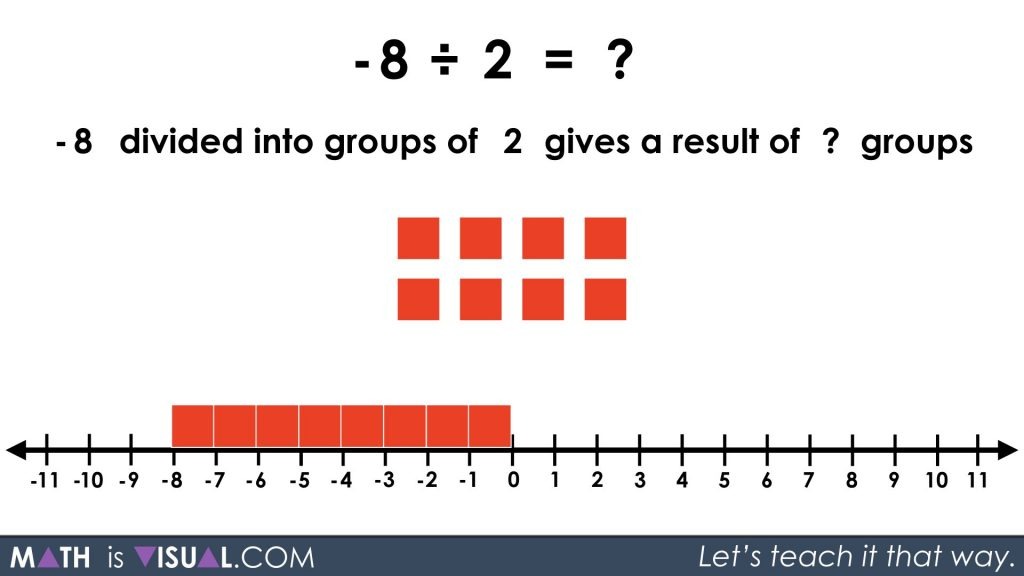
Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt

The problem we run into here is that we want to determine how many groups of +2 we can create from -8.

This is a problem because we can’t make any groups of +2 (or so it may seem).

If we determine first how many groups of -2 we can make (4 in total), we can negate the negative of each group by using negatively charged groups:

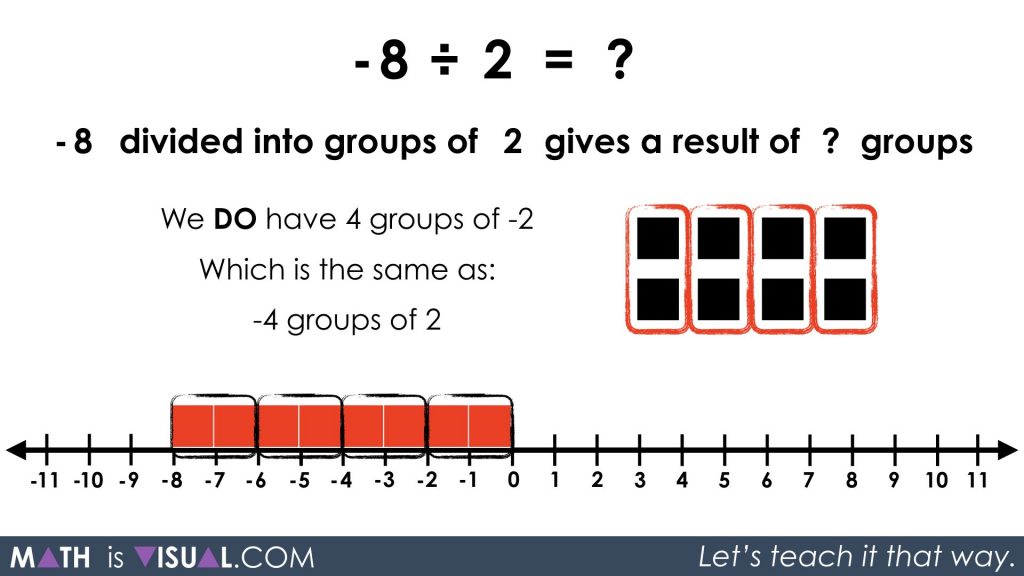
Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution

So instead of having 4 positively charged groups of -2, we can express those groups as 4 negatively charged groups of +2.

In other words, we have:

-4 groups of 2

Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution 2

Other possible representations and strategies:

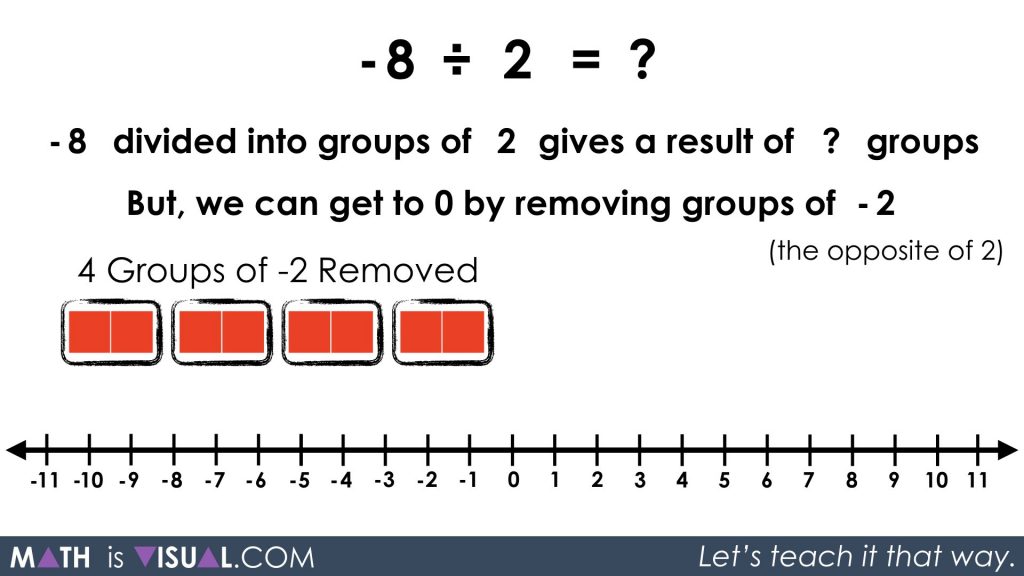
Consider determining how many groups of -2 we can “remove” since division represents repeated subtraction. Once we find out how many groups of -2 we can remove, we can then express those groupings negatively to create positive values in the groups:

Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution 3

Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution 4

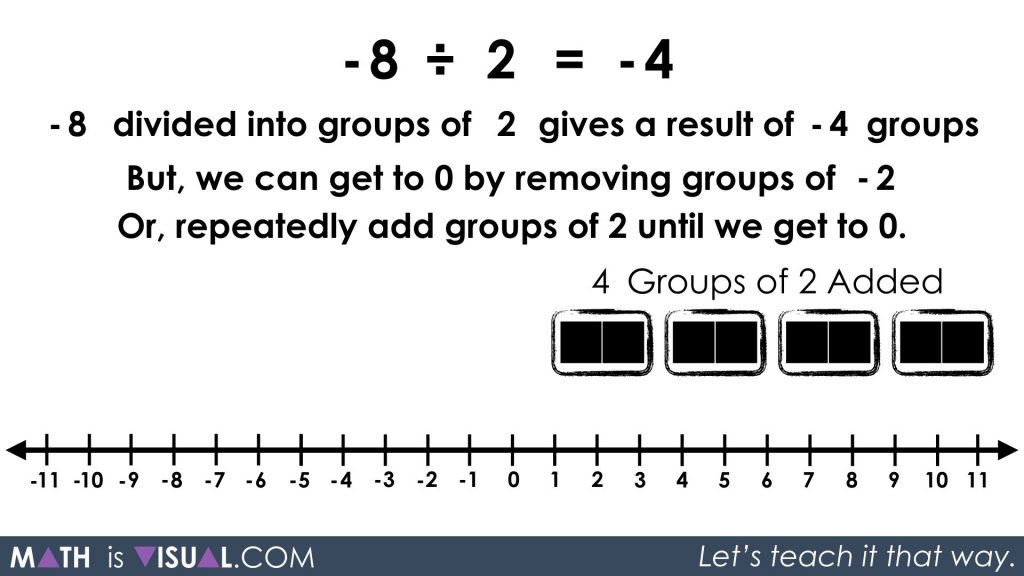
We can also think about how many groups of 2 we can “add” to get to 0:

Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution 5

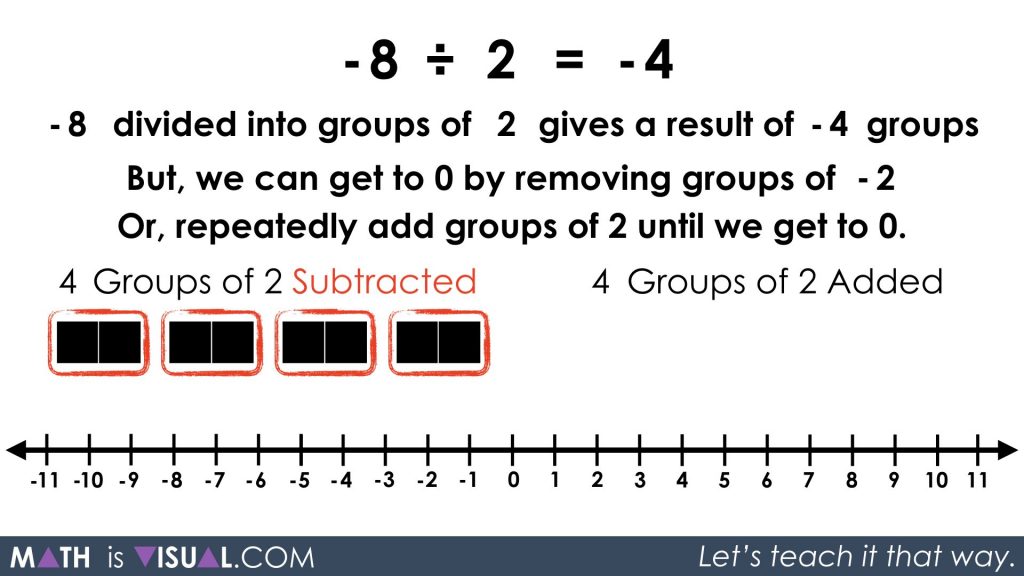
Since repeated addition is the opposite operation of repeated subtraction, we can then take those groups and “subtract” them by negating the groupings:

Integer Division - Negative Divided by Positive quotative -8 divided into groups of 2 prompt solution 6

Visual Prompt #3: Your Turn!

Pause the video and let the viewer apply their knowledge of negative by a positive partitive division using the following visual prompt:

-10 ÷ 5 = ___

or

-10 divided into 5 groups gives a result of ___ per group

Integer Division - Negative Divided by Positive partitive -10 divided into 5 groups prompt

Allow time for the viewer to engage in the partitive division before showing the remainder of the video animation or the following still image.

Again, we must note that we want to determine the value of the quantity that will be shared amongst 5 groups.

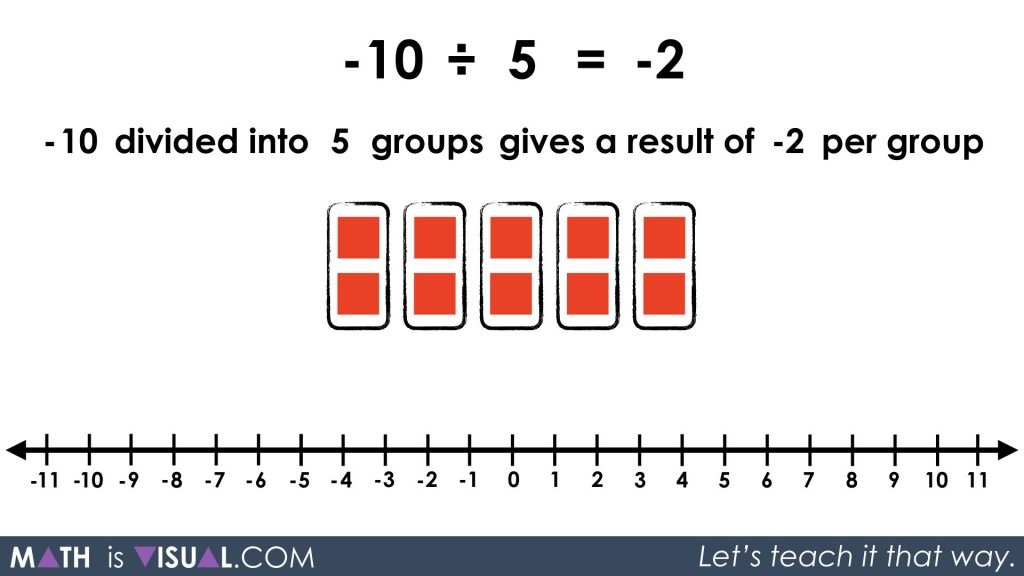
Integer Division - Negative Divided by Positive partitive -10 divided into 5 groups prompt solution

By fair sharing -10 across the 5 groups, we see that each group will have a value of -2.

How about approaching the same problem from a quotative approach:

-10 ÷ 5 = ___

or

-10 divided into groups of 5 gives a result of ___ groups

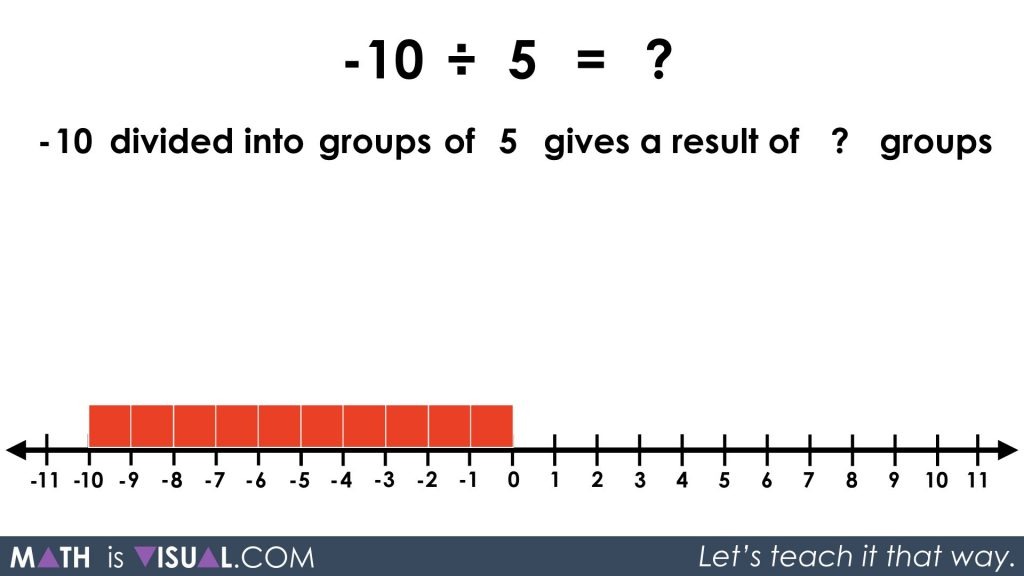
Integer Division - Negative Divided by Positive quotative -10 divided into groups of 5 prompt

By using our conceptual understanding built through the previous visual prompts, we can now recognize that since there are 0 groups of +5 we can create from the -10 given, we must use negatively charged groups.

Since I can create 2 groups of -5, I know I can also represent those same 2 groups as -2 groups of +5.

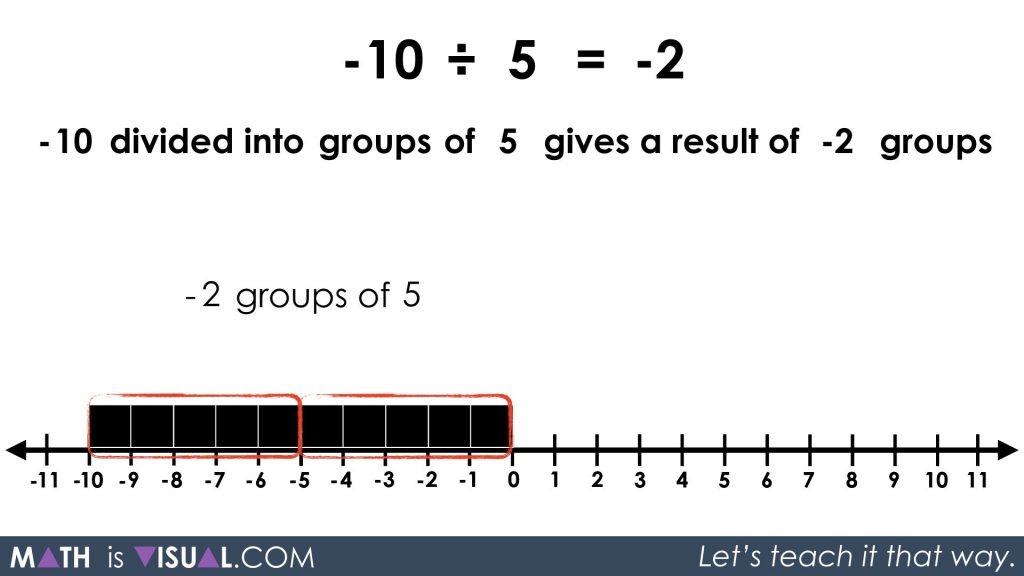
Integer Division - Negative Divided by Positive quotative -10 divided into groups of 5 prompt solution

Wow! Division of integers is pretty complex stuff! Let’s not rush it. Give your students a chance to toy with these ideas and really build a deep understanding of how integers behave both concretely and visually before allowing them to come up with their own student generated rules and algorithms that they can apply moving forward.

Only one more post left in the division of integers series.

Thanks for sticking around!

Math IS Visual. Let’s teach it that way.