In this series of Math Is Visual Prompts, students are given the opportunity to start solving one-step equations and explicitly identifying the type of division that each context lends itself to: partitive or quotative.
Need more help with partitive or quotative division? Check out this 3 act math task division unit that unpacks both types in a conceptual way.
We also do our best to model this using the linear model of a number path (precursor to the number line) as well as abstractly using numbers and symbols.
As always, the visuals provided as a consolidation are useful AFTER students are given the opportunity to work with these ideas concretely and after consolidating in the classroom through student work.
Let’s get started…
Sparking Curiosity: Conceptual Subitizing Number Talk
First, we introduce this series of visual prompts with a really low floor by showing 4 columns of 3 squares, one column at a time before covering them up:
Students are then tasked with convincing their partners of how many squares they observed and how they know.
Then, we “slide in” a couple of red solo cups:

The question now becomes:
How many are under each cup if the squares were divided amongst the cups evenly?
When you actually provide the concrete manipulatives for students to use, this is a pretty easy activity and all students can access this task.
When you ask students, everyone will say “6”, which is great!
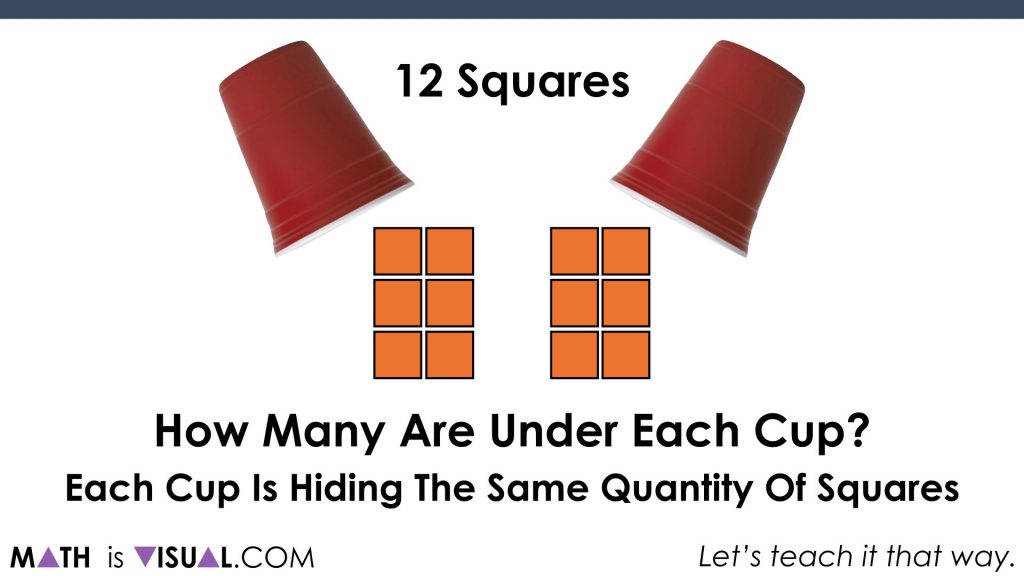
However, we want to make sure that they are clearly articulating what is happening here.
Here’s one way to do so using a number path (i.e.: a concrete number line):
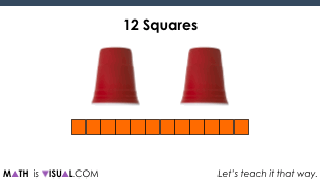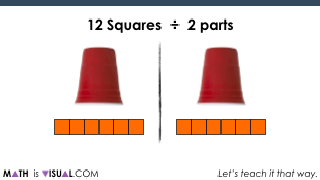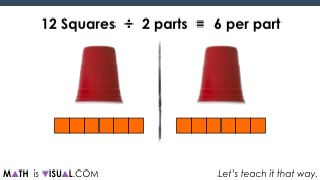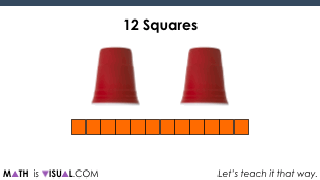
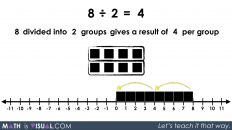
Something students (and teachers) can easily miss is that this is a specific type of division known as partitive division.
Want to learn more about partitive and quotative division? Check out my post on tapintoteenminds.com about the progression of division here.
Now, by all means, we need to help students build procedural fluency over time from conceptual understanding. So, if you feel that time is now, you can also consolidate how to connect it to numbers and symbols abstractly:
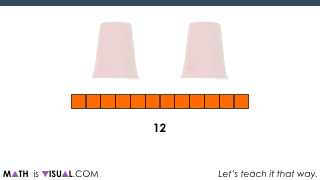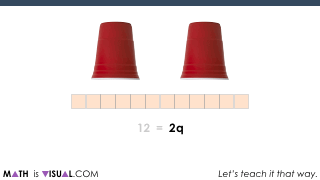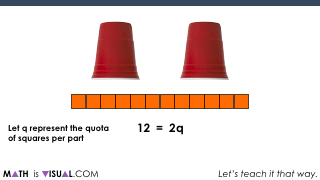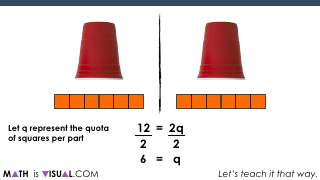
If I can recommend anything about partitive division is really being explicit about the fact that you are actually dividing by partitioning the quantity into parts (or groups).
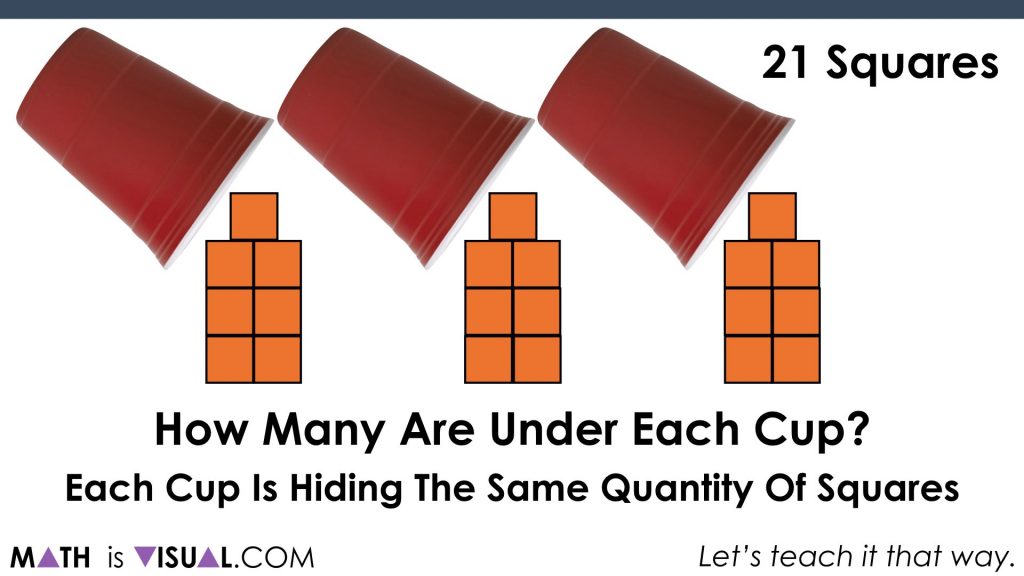
Challenge #2: Another Partitive Division Scenario
Here we go:

Again, students will quickly determine that the number of squares under each cup must be 7.
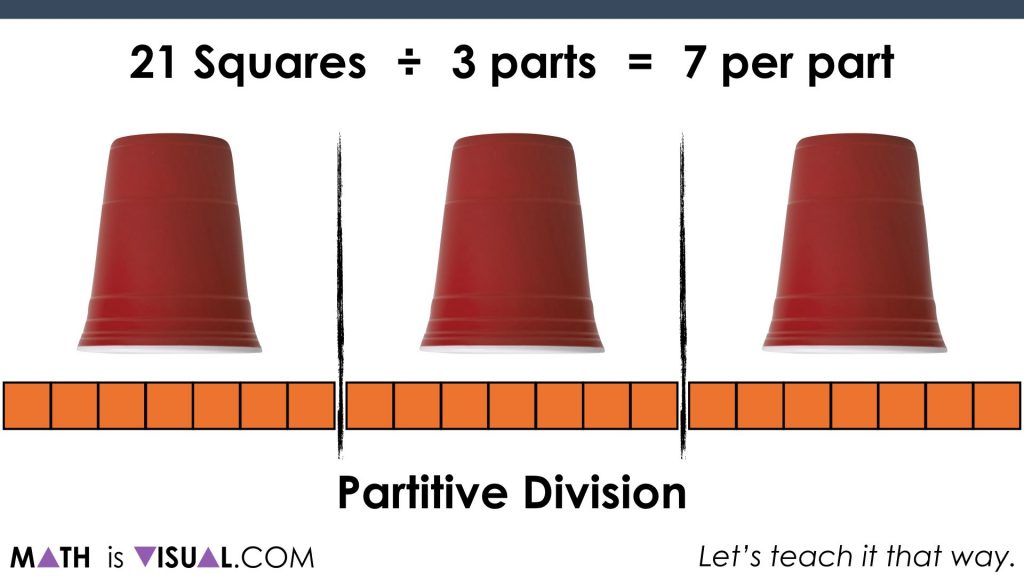
Again, the key here is emphasizing that you are using partitive division to partition the quantity into 3 equal groups (or fair sharing the cubes to the 3 glasses).
The video visual prompts also unpacks the symbolic notation as well.
Challenge #3: Quotative Division Scenario
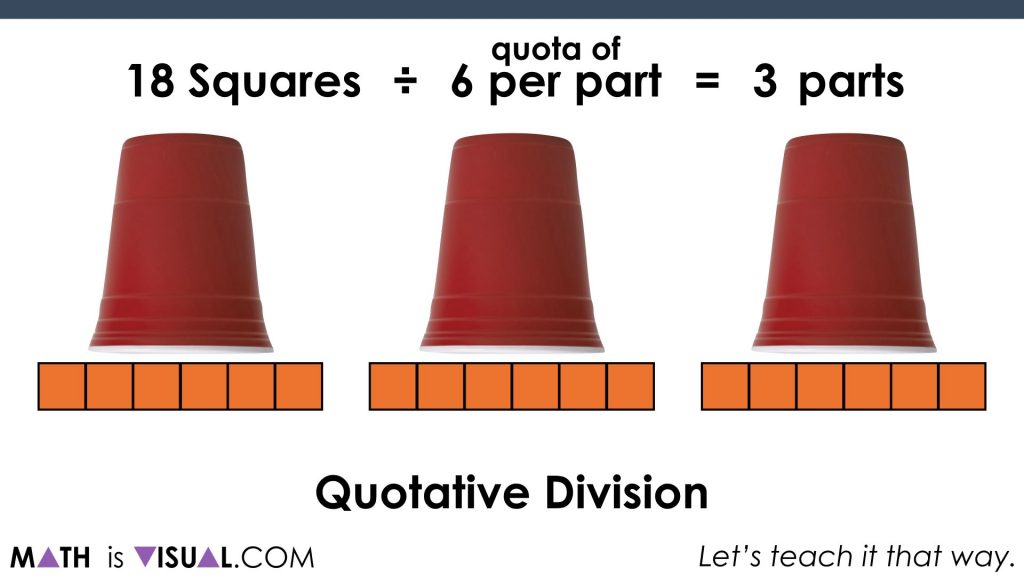
Now, we move on to a quotative division scenario. With quotative division, we are dividing by the known “quota” or the desired number in each group. When you say “3 ‘gusinta’ (goes into) 21 how many times??” you are using quotative division language.
In this challenge, we are asking:
How many glasses (parts) can you divide 18 squares into if there must be 6 per glass (part)?

You’ll notice that with this problem, you can’t use partitioning as a strategy to solve UNLESS you already know the answer due to automaticity or through some other means.
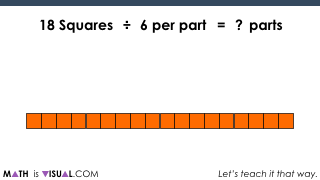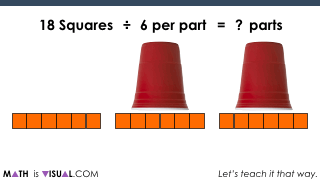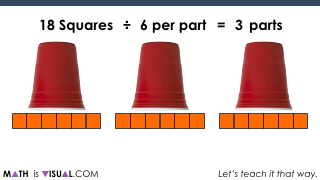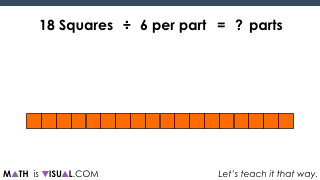
You’ll note that when you are using quotative division, you’re using repeated subtraction (or iterating up from zero, like you’re multiplying).
Be sure to check out the visual prompts video at the top of the post to get the FULL EFFECT including “pause bars” to allow you to pause the video and let kids have think / discussion time.
How’d It Go?
Thanks for watching and reading!
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Interested in diving into problem based units to explore both types of division? Dive into a problem based unit that explore partitive and quotative division here.
Math IS Visual. Let’s teach it that way.
Be sure to dive into our engaging math lessons that Spark Curiosity and Fuel Sense Making through the use of visuals.




When we teach this concept, we call partitive division “fair share” and we call quotative division “how many fits in.” This helps a lot when teaching division of fractions and decimals. If you have 5/6 divided by 1/2, you can ask how many 1/2 fit in to 5/6? If you have 3/4 divided by 2, you can ask yourself, if I divide 3/4 into two pieces, how much would each piece be worth? It really helps with estimating too. And students can really see why sometimes division results in a larger answer and sometimes it results in a smaller answer.
Great points, Leslie! Yes, “fair share” is another common term for partitive and it is great for students to have more than one perspective when they think about the two types of division.
Partitive can be helpful for connecting to the word “partition” since we are “partitioning” the quantity into a specific number of “parts” (or groups) whereas quotative is when we know the “quota” or “how many” are in each group.
Something interesting to consider is that when you use partitive division, you are essentially revealing a rate. Thank John Van De Walle for that one! 🙂
So correct me if I am wrong. For the connection to the symbolic, the variable is defined one way or the other, as the quota per part or the # of parts. The coefficient of the variable is the number of parts in the case of the variable being the quota per part and the number in a quota in the case of the variable being the # of parts. (OK, that was hard to write, lol) . In other words, once you define your variable as one type of division, then the coefficient represents the other.