In the previous integer multiplication post, I thought that I was ready to move on from integers to other concepts. However, very quickly I had emails from the Math Is Visual community asking when the division of integers videos were going to be released. That set me on a very long journey to uncover and conceptualize integer division for myself prior to attempting to create visuals that might help others better understand division of integers.
So, in the next few posts, I will be tackling the very complex world of integer division from the two possible perspectives: quotative and partitive division. This video and the coming integer division posts will be added to the integer operation series. In this video, we will first address quotative (or measured) division and partitive (or fair share) division with the dividend and divisor both positive.
Although this might seem “beneath” your students if you’re looking for integer division, you really do want to start here because many students do not realize that there are two types of division that can take place. This will be very difficult to understand while also progressing through the integer division concepts simultaneously.
See the instructional guide below aimed to help teachers and/or parents use this activity with their own students/children.
Helpful Definitions:
Dividend – A number to be divided by another number.
Divisor – A number by which another number is to be divided.
Quotient – The result obtained by dividing one number by another number.
Quotative Division – When dividing a number into groups of a measured quantity. For example, when we divide 8 into groups of 2 and we want to determine how many groups that will make. Also known as measured division since you have already measured the quantity of each resulting group. When speaking with Zal Usiskin from University of Chicago, he described quotative division as “rate” division since you are dividing the quantity by a rate (i.e.: a quantity per group).
Partitive Division – When dividing a number into a known number of groups. For example, when we divide 8 into 2 groups and we want to determine how many items each group will have. Also known as fair share division since you are dividing up the quantity evenly amongst each group. Usiskin described partitive division as “rate quotient” division since the result will be a rate.
Visual Prompt #1: Quotative Division
In the video above, we start with whole number, quotative division as a low floor start:
8 ÷ 2 = ?
We show that we can approach this problem from two different perspectives:
8 divided into groups of 2
or
8 divided into 2 groups
Although the result will be the same number, conceptualizing how the division takes place is very different for both of these situations.
So, let’s have the viewer model concretely and/or visually the following:

Students may use spatial reasoning to create groups of a set or linearly on a number line. They may also consider using repeated subtraction to repeatedly take away groups of 2 until all are removed (or 0 remain).
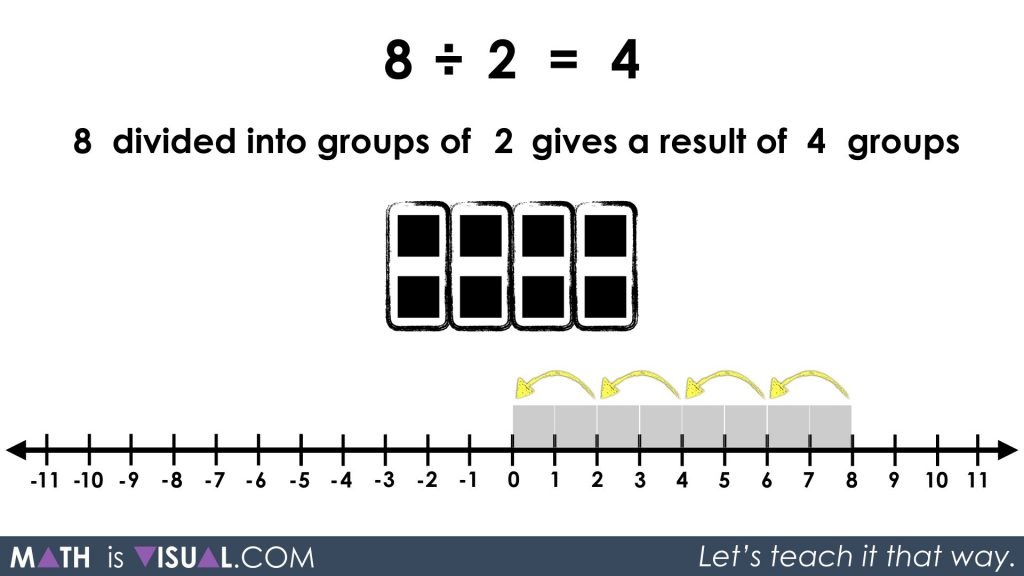
The arrow can also be pointing to the right if students use repeated addition to repeatedly add groups of 2 from 0 until they reach 8.
Visual Prompt #2: Your Turn!
In the second visual prompt, pause the video at this frame where the viewers are given an opportunity to apply their understanding of whole number quotative division to the following prompt:
9 ÷ 3 = ___
or
9 divided into groups of 3 gives a result of ___ groups

You can then view a visual animation of the solution in the video or reveal this frame:
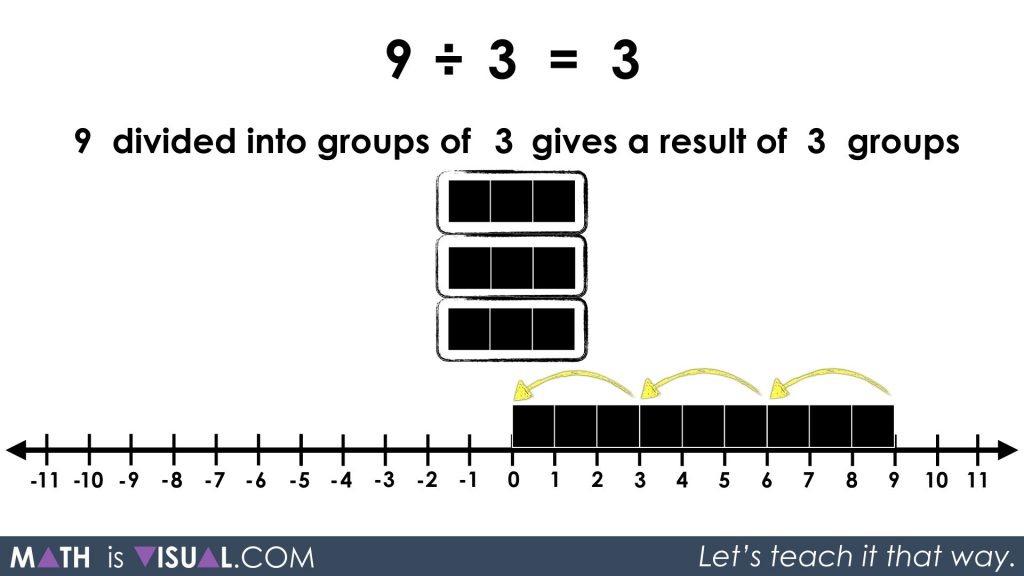
Visual Prompt #3: Partitive Division
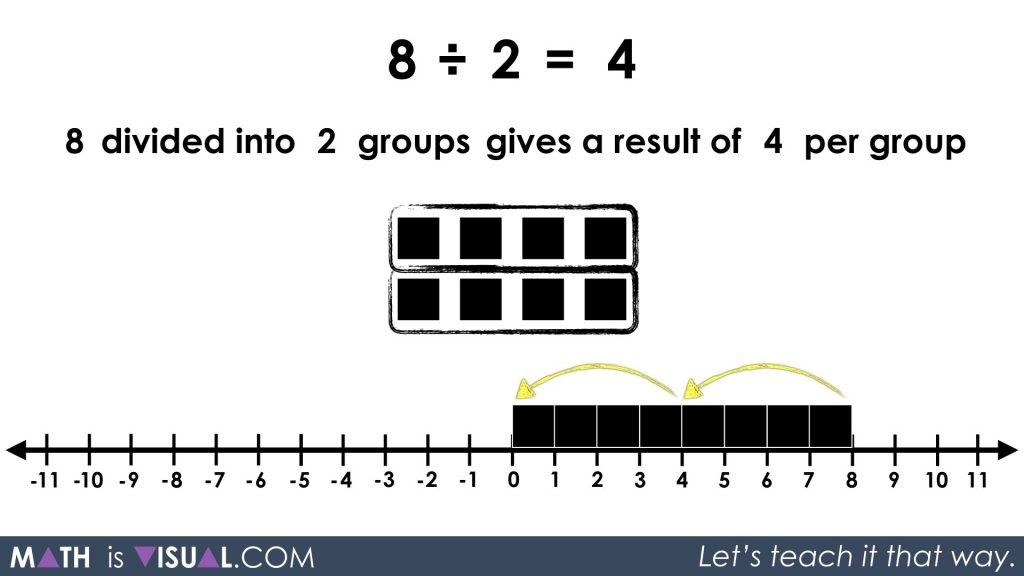
Now we move on to approaching the same problem from a partitive division perspective:
8 ÷ 2 = ____
or
8 divided into 2 groups gives a result of ____ per group.
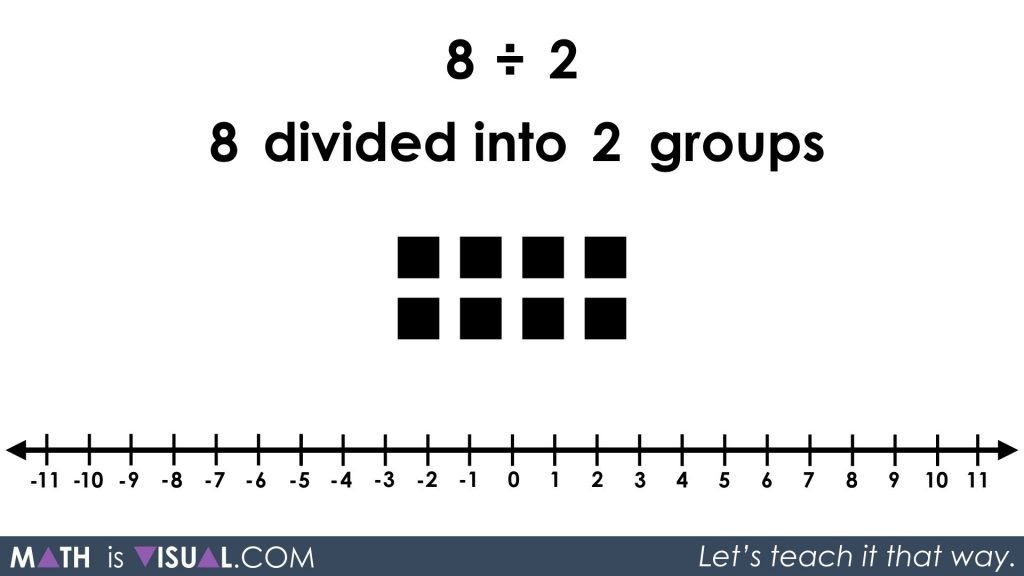
Although the value of the result will be the same, the conceptual understanding and concrete/visual approach will look very different.
Similar to above, we can approach this using a set or linear model where we are spatially splitting the quantity into 2 equal groups and counting the number of objects in each group. While the visual below may look awfully similar, note that the use of repeated subtraction might be a bit different because we do not know how many are in each group (yet). So, the repeated subtraction may consist of fair sharing 1 object at a time or 2 objects at a time, up to a quantity that a student is comfortable to subitize quickly for sharing out.
Visual Prompt #4: Your Turn!
Pause the video and let the viewer apply their knowledge of whole number partitive division using the following visual prompt:
10 ÷ 5 = ___
or
10 divided into 5 groups gives a result of ___ per group

Allow time for the viewer to engage in the partitive division before showing the remainder of the video animation or the following still image:
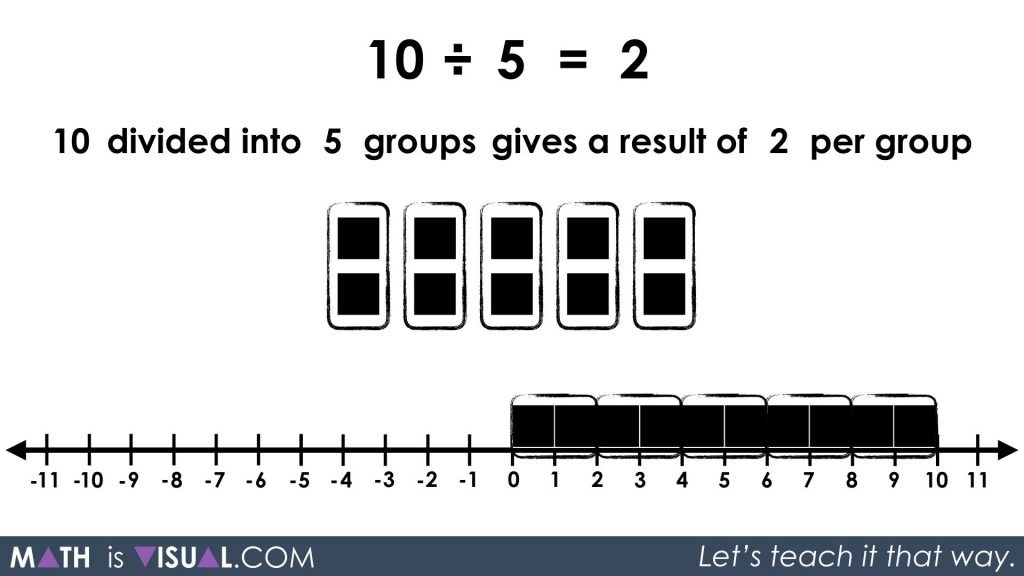
Well, there you have it; quotative and partitive division with whole numbers.
Are you ready to take these two concepts into the land of integers?
It’s coming soon, so watch for it!
Math IS Visual. Let’s teach it that way.




Based on my experience with 3rd, 4th, and 5th graders, the number line as a strategy for determining the quotient is only useful for quotative division (when you know the size of the jumps to make on the number line). Of course, once a quotient has been found, the number line can be used as a second strategy or a way to check/prove that the quotient is correct.
You can also use a number line for partitive division by “partitioning” or creating equal “parts”. This is helpful for students to build spatial reasoning skills as well as building an understanding of how numbers relate to one another.
[…] In this series of Math Is Visual Prompts, students are given the opportunity to start solving one-step equations and explicitly identifying the type of division that each context lends itself to: partitive or quotative. […]
[…] Is Visual Prompts, students are given the opportunity to start solving two-step equations with partitive division through the use of cups to hide “squares” or connecting cubes where the cups […]
[…] Visual Prompts, students are given the opportunity to start solving two-step equations with both partitive and quotative division using typical word […]
I definitely understand that there can be two different unknowns of the number of groups or the number in the groups. I think it would be helpful if we taught kids to set up the question the same way all of the time. For example if we always had the total divided by the number in each group equals the number of groups. If we use the defintion that division is the opposite of mult. then it makes sense to do this. ( long division does this). It also makes sense we subtract apples from apples not groups from apples. Once the setup is clear students can be taught that they can change the way to solve ( fact family). It just seems to make word problems easier to figure out what is to be solved.
[…] While it might seem obvious that we are simply dividing 7 cups of water amongst 5 mugs, what might not be so obvious initially is that there are two types of division. […]
the audio is not working…
Hi Thelma! Sorry about the mixup – but these are all “silent solution” videos where they are just a series of visuals. You can use them for a math talk in your class or at home so you can do the facilitating! 🙂
[…] If you’re interested in getting a quick understanding, then check out this set of visual prompts unpacking the two types of division conceptually. […]