In This Set of Visual Number Talk Prompts…
Students will extend growing linear visual patterns, make near and far predictions and describe visual patterns in words.
Intentionality…
Students will engage in a visual number talk using geometric patterns to develop a deeper understanding of the following big ideas.
- Patterns can be extended because they are repetitive by nature.
- Pattern rules are generalizations about a pattern, and they can be described in words.
- A pattern can be extended to make a prediction.
- For far predictions, calculations are required for efficiency.
- In a growing pattern, the values increase.
- In a linear pattern, the values increase at the same rate.
- Graphical representations of linear growing patterns appear as straight lines.
String of Related Problems
Present the following visual patterns through the visual number talk prompt videos below. Leverage the day one context of an animal hoarding nuts, seeds or fruit in preparation for the winter. For each pattern, ask students to describe the pattern rule in words and predict the value of the 14th day and 21st day. Students are encouraged to justify their thinking and educators are encouraged to facilitate this visual number talk by modelling student thinking using the mathematical model that will help give others a window into that thinking.
While the array model or area model would best suit the visual patterns shared and therefore we want to be intentional about seeking ways to best emerge the use of this model, be sure to acknowledge other models that students may have used including linear or symbolic models.
Look for opportunities to build efficiency. For example, rather than counting on or repeated addition, can students use partial products through scaling in the table? For example, the 14th term in the first pattern is the same as the fifth term, multiplied by two, plus the 4th term. Or see the multiplicative relationship between the term number and the term value? Facilitator note: The pattern rule can be described two ways. For example, start at 3, add three each time. Or multiply the term number (in this context, the day) by three (the rate).
Visual Number Talk Prompt
Student prompt:
Use manipulatives or draw what you think might come next.
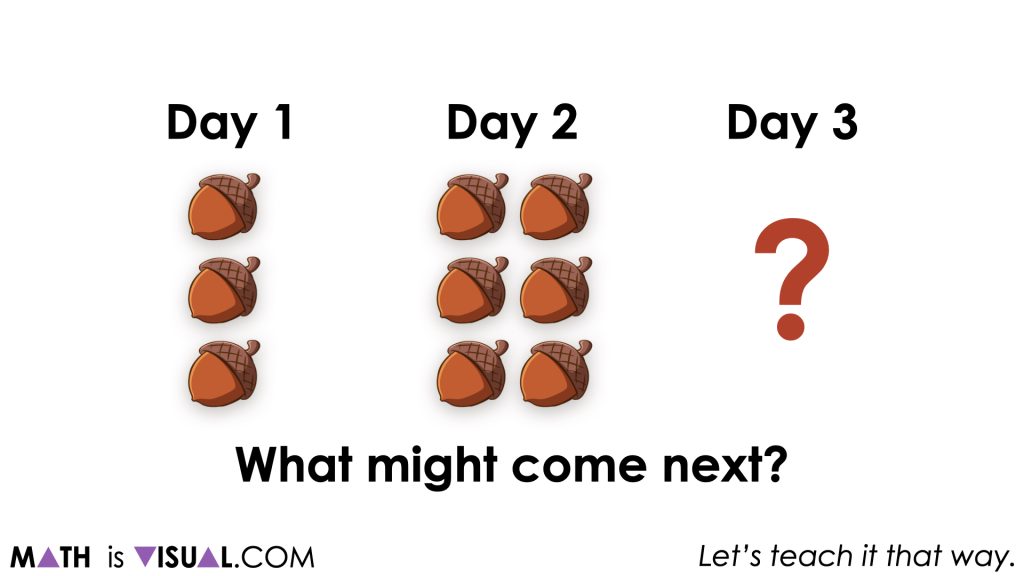
At this point, it is important for students to understand that there is really no way to guarantee what will come next because we do not have enough information yet. Here are some of the predictions students might make and some possible reasoning:
- 9 acorns because the pattern is growing by 3 acorns per day;
- 12 acorns because the pattern is doubling each day.
- 3 acorns because the pattern is repeating; and,
- Other possibilities.
Next, show students the number of acorns in total on day 3 and ask them to make another prediction for how many acorns there will be on day 4.

You may notice that more and more students update their predictions to a pattern increasing by 3 acorns per day (a rate of 3 acorns/day).
Once we share how many acorns were collected over the first four days, we can ask students:
Assuming this pattern continues, describe the pattern rule in words to your neighbour.

As students continue discussing how they might describe the pattern rule, you can extend this prompt to:
Describe what day 14 and what day 21 will look like.

Articulate to students that the purpose of a pattern rule is to help someone easily understand how a pattern changes from day to day (or stage to stage, or figure to figure). In the case of a geometric pattern (or visual pattern), it is also helpful to describe how the visual pattern is growing without necessarily being able to “see” the pattern with their own eyes.
Some students might be able to articulate that day 14 should be a long 3 acorn by 14 acorn rectangle.
Since we promote students building number fluency and flexibility each and every day, this is an excellent opportunity for them to apply the multiplication strategy of partial products which leverages the distributive property to decompose the factor of 14 into smaller parts.
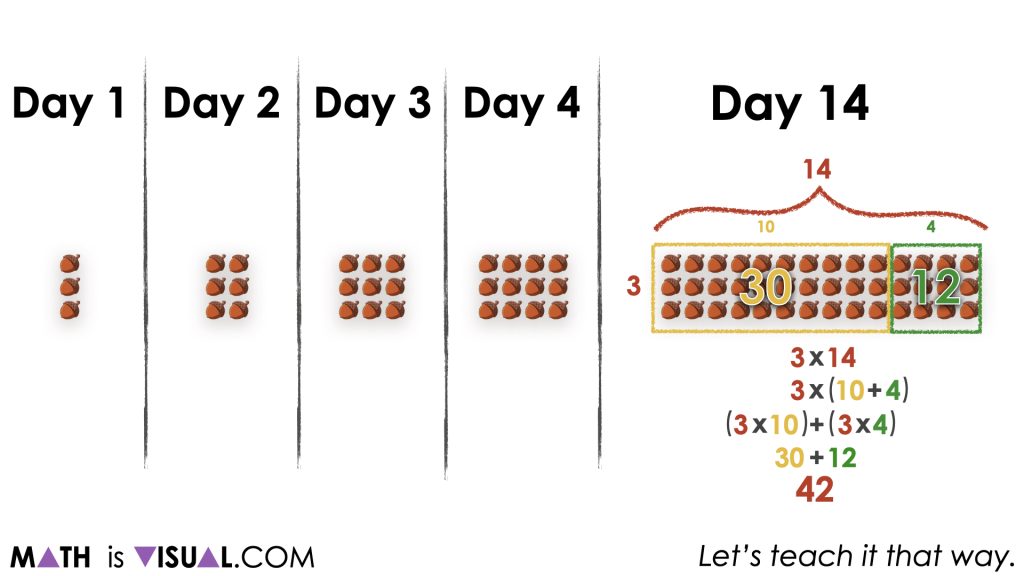
Above, you can see that this particular example shows 14 acorns decomposed into parts of 10 and 4 which ultimately produces the following equivalent expression:
3(10 + 4)
Not only does this promote an opportunity for students to multiply without a calculator to build fluency and flexibility with multiplication, but it also allows us to revisit order of operations and how blindly following the rules can actually create more work for us at times.
For example, if we simplify what is “inside the Brackets” (or Parentheses) as BEDMAS (or PEDMAS) would require, we would actually be doing ourselves a disservice.
Here, we know that 3 groups of 10 acorns is 30 acorns and 3 groups of 4 acorns is 12 acorns, resulting in 42 acorns total.
Of course, students are not limited to the distributive property here and are more than welcome to leverage other multiplication strategies such as doubling and halving or other strategies that feel helpful.
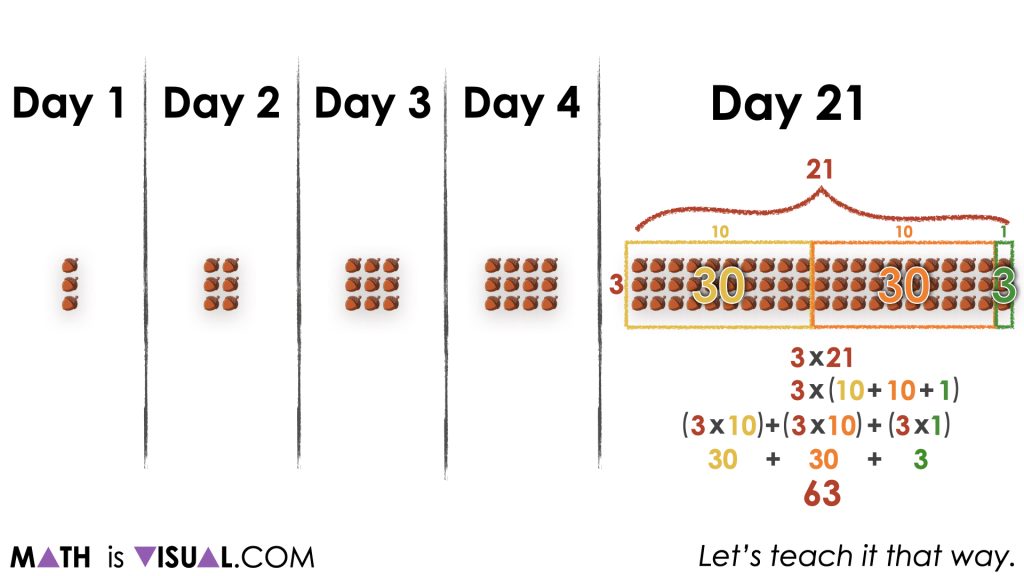
The description of day 21 is similar to that of day 14 and students might leverage similar or different multiplication strategies to yield their total number of acorns.
Want to Explore These Concepts & Skills Further?
Two (2) additional number talk prompts are available in Day 2 of the Acorn Hoarding problem based math unit that you can dive into now.
Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.
Did you use this in your classroom or at home? How’d it go? Post in the comments!
Math IS Visual. Let’s teach it that way.

![Planting Flowers [Day 2] - Revealing a Rate Through Partitive Division MIV Featured GIF](https://mathisvisual.com/wp-content/uploads/2021/07/Planting-Flowers-Day-2-MIV-Featured-GIF-232x130.gif)
Add comment