Scaling Ratios to Solve Proportions

In This Set of Visual Number Talk Prompts…

Students will identify proportional relationships and apply ratio reasoning to scale in tandem to find unknown quantities. Through this investigation, we will emerge the idea of a scale factor and how it can be used to set up and solve proportions.

Intentionality…

The purpose of this set of visual number talk prompts is to build fluency and flexibility with ratio reasoning through scaling in tandem and to extend this understanding to setting up and solving proportions by revealing scale factors. In particular, the following big ideas may emerge:

• There are two types of ratios; composed unit and multiplicative comparison;
• Thinking of a ratio as a multiplicative comparison involves describing a quantity as “a number of times greater than another” or describing a quantity as “a fractional part of another” and often (not always) involves a ratio comparing quantities with the same units;
• Ratios can be scaled in tandem to reveal an infinite number of equivalent ratios;
• Although all ratios can be scaled in tandem, ratios thought of as a composed unit lend themselves more naturally to scaling;
• Quotative division is applied when trying to determine a scale factor between two quantities/measures of the same unit (i.e. packs of paper and packs of paper, height and height);
• Scaling ratios in tandem is thought of as a type of ratio reasoning;
• An equation of two equivalent ratios is known as a proportion; 
• An unknown quantity from a proportion of equivalent ratios can be found by using quotative division to reveal a scale factor between two corresponding known quantities from both ratios; 
• A variety of mathematical models can be used as a tool for solving problems involving a proportional relationship and as a way to represent or prove your thinking. Some of these mathematical models include double bar/double number line models, ratio tables, two variable graphs, and equations; 
• The graph of a proportional relationship is linear and crosses through the origin, (0, 0); and,
• The graph is helpful for identifying a trend or relationship between variable quantities and can be helpful when seeking to approximate the value of unknown quantities in that trend and/or relationship.

String of Related Problems

The following sequence of problems provides an opportunity for students to apply their ratio reasoning skills to scale in tandem given a proportional relationship involving a composed unit ratio between distance in kilometres and time in minutes. 

This context was intentionally selected to promote the use of a linear model like a double bar or double number line model to emerge scaling in tandem. Since this context involves a composed unit ratio – a ratio that can be thought of as a single unit and lends itself to scaling up and down – scaling in tandem is a helpful tool to not only determine unknown quantities, but to also promote student flexibility and fluency with multiplicative thinking. 

Throughout this series of visual number talk prompts, be sure to avoid rushing to setting up and solving a proportion as that will defeat the intent of this string of related problems.

If the terms ratio reasoning, composed unit ratios, scaling in tandem and multiplicative thinking are foreign to you, consider deepening your understanding of proportional reasoning by taking our course, The Concept Holding Your Students Back: Unpacking Key Understandings In Proportional Reasoning So You Can Reach Every Student.

Visual Number Talk Prompt

Student prompt:

A car travels 24 kilometres every 15 minutes.
How far would the car travel in 5 minutes?
Craft a convincing argument without the use of a calculator.

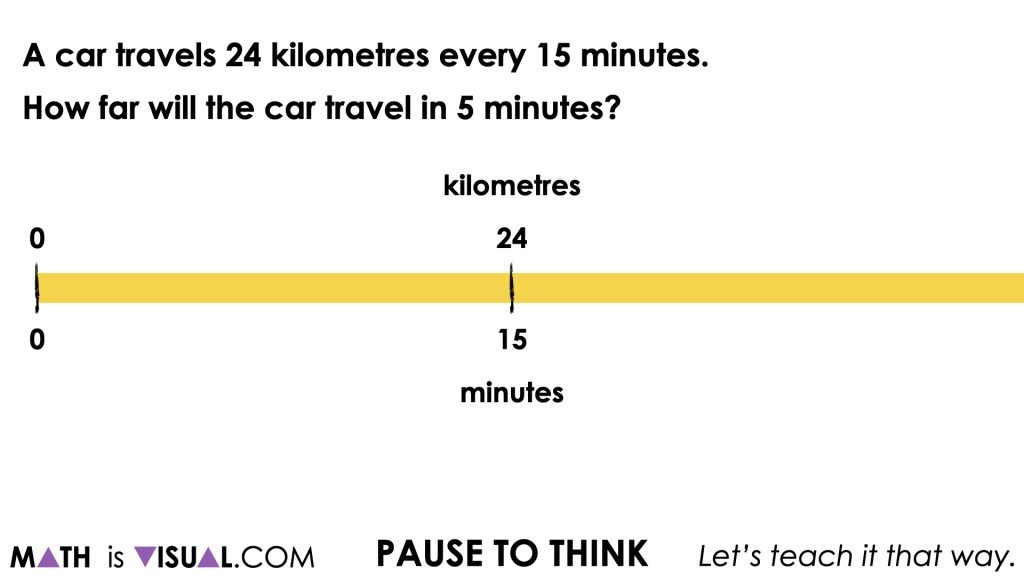
With this visual up for all to see, give students a reasonable amount of time to reflect on what this question is asking them and to leverage their understanding of magnitude of number to spatially approximate where 5 minutes and the corresponding number of kilometres travelled should be placed on the double number line.

The goal here is to give students a low floor opportunity to leverage their understanding of magnitude as well as to emerge the fractional thinking necessary to determine that 5 minutes is 1 third of 15 minutes. 

Since we are working with a composed unit ratio, 24 kilometres to 15 minutes, there are an infinite number of equivalent ratios that exist in this proportional relationship. The ratio x to 5 minutes is only one of those equivalent ratios. 

Without much prompting, students should come to the conclusion that since 5 minutes should be placed 1 third of the distance between 0 minutes and 15 minutes, then the number of kilometres travelled 1 third of the distance between 0 kilometres and 24 kilometres should be 8 kilometres.

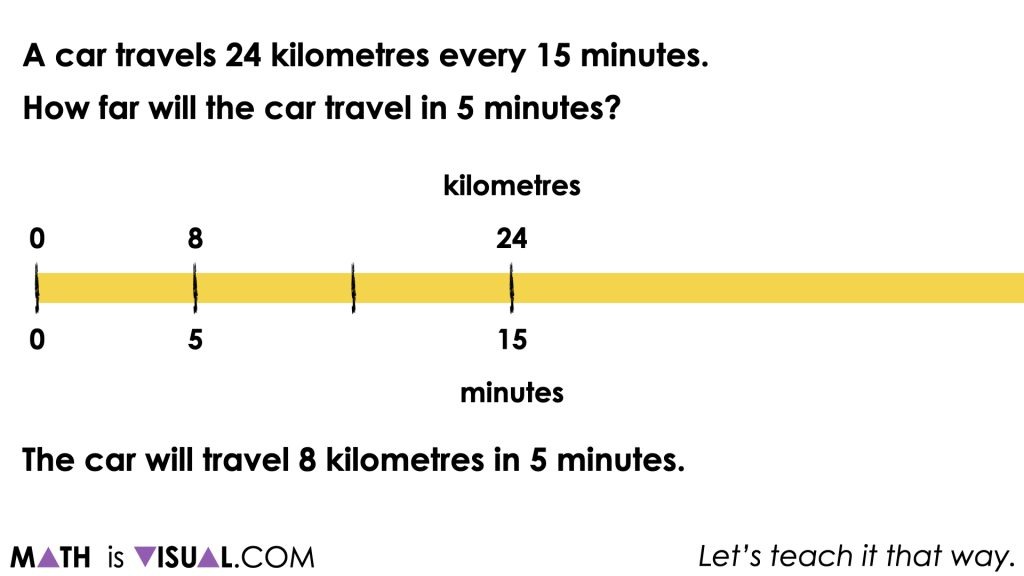
Note that while some students may be using multiplicative thinking (i.e.: knowing 5 is 1 third of 15), others may be using more of a guess and check approach with additive thinking (i.e.: skip counting by 4s, then 5s to realize that adding 5 repeatedly will get me to 15). Be supportive of any and all strategies students bring to the table, but think of the purposeful questioning you might use to nudge each student forward towards more efficient or “clever” approaches without sounding negative or discouraging.

Something that the facilitator should be able to notice and name here is that the missing quantity that students have solved for here is the same quantity that they would determine when solving this proportion: 

There should be no rush at this point to show students that they have just solved a proportion of equivalent ratios unless students are arriving in your class having already been exposed and/or rushed to an algorithm like cross multiplying, “magic circle” or any other set of steps that they do not understand conceptually. While we will not shut students down from using a trick they have learned previously, we do want to encourage them to work towards crafting a convincing argument as to why their answer is correct. If they cannot convince someone of why their method works, then we can deem their approach a “trick” rather than a justifiable strategy.

Want to Explore These Concepts & Skills Further?

Three (3) additional number talk prompts are available in Day 2 of the Stacking Paper problem based math unit that you can dive into now. 

Why not start from the beginning of this contextual 5-day unit of real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.