Revealing Equivalent Ratios By Scaling In Tandem

In This Set of Math Visual Prompts…

Students will reinforce concepts related to ratios and to explore how quantities covary by finding equivalent ratios through scaling in tandem.

Intentionality…

The purpose of Day 2 activities is to reinforce concepts from Day 1. Students will engage in a visual number talk that will encourage them to consider different ways to describe relationships between quantities and reinforce the idea of scaling in tandem to reveal equivalent ratios.

Students will also have an opportunity to complete a purposeful practice that will serve to develop a deeper understanding of the following big ideas:

• A ratio is a multiplicative comparison between two or more quantities;
• There are two types of ratios; a composed unit ratio and a multiplicative comparison ratio;
• A composed unit is often (not always) a ratio with two distinct units;
• Unknown quantities in a ratio relationship are often most efficiently revealed through multiplicative thinking strategies rather than additive thinking strategies;
• A composed unit ratio can be scaled in tandem;
• Ratios can be constructed by comparing a part to its whole (part-to-whole) or comparing a part to another part of the whole (part-to-part).
• Ratios can be represented using the separator “to” or a colon “:”. Two quantities from a ratio relationship can also be represented as a quotient through the use of the division symbol “÷” or with the fraction bar.
• When you divide two quantities in a composed unit ratio through partitive division, you reveal a rate.
• Equivalent ratios are derived from the same rate;
• An infinite number of equivalent ratios can be revealed to assist in determining an unknown quantity from a ratio relationship; and,
• Ratio problems can be represented and solved using a variety of strategies, tools, and representations.

Preparing to Facilitate This Number Talk

The following visual math talk is a string of related problems that are crafted in a way to foster discussion and the construction of viable arguments. As such, they are open ended and have more than one possible response.

As the facilitator of the following visual math talk prompts, be prepared to notice and name the thinking students are using (i.e.: additive thinking or multiplicative thinking).

While you could simply share the first image with the prompt for students, introducing via the silent solution animations provided may be more helpful. Although each visual math talk prompt video models a possible strategy, we encourage you to represent student thinking by drawing on the board or on the screen rather than simply playing the video and ignoring the thinking of your students.

Visual Math Talk Prompt #1

Consider utilizing the following visual math talk prompt and be prepared to pause where indicated:

Prompt:

What do you notice? What do you wonder?

After students share some of what they notice and wonder about the shapes that have ‘popped’ on the screen, continue playing the video until the next prompt appears:

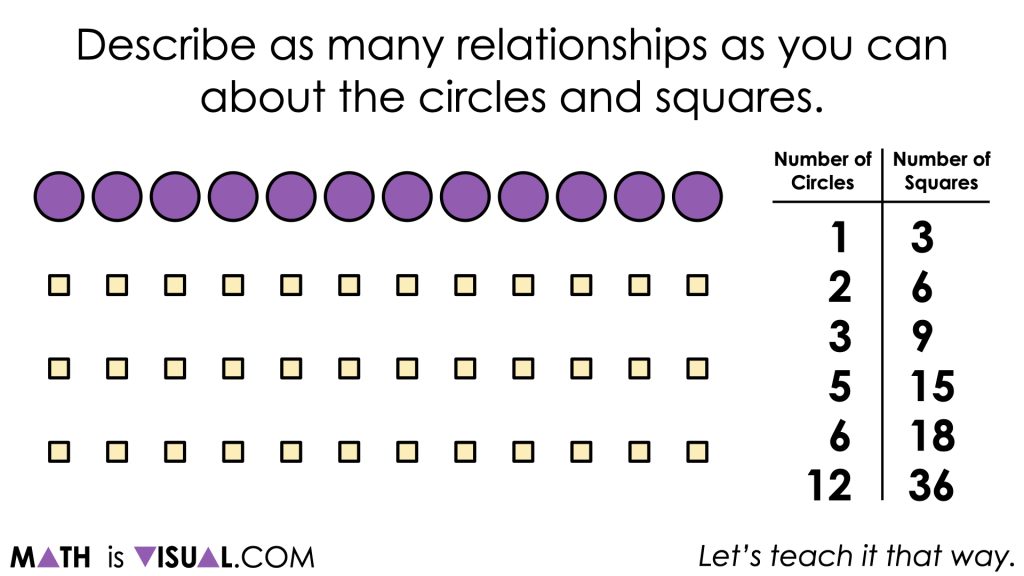
Describe as many relationships as you can between the circles and the squares.

• Some possible relationships students might share include:
• There are 10 more squares than circles
• There are 3 times as many squares as there are circles
• For every circle there are 3 triangles
• ¾ the shapes are squares (¼ of the shapes are circles)
• 75% of the shapes are squares

It is worthwhile to note the observations that students will share, as a way of determining if students are thinking in absolute or relative terms, and whether they are able to consider both part:whole and part:part relationships.

As you are making note of students’ observations, consider modeling the use of ratio language and notation, including:

• The ratio of ____ to ____ is _____ : ______. For example, “the ratio of squares to circles is 3:1 or the ratio of circles to squares is 1:3”.
• For every ______, there are ______.

Some students may make use of rate language such as:

• There is a rate of _____ per _____
• For example, “there is a rate of 3 squares per circle” or “there is a rate of 1 third circles per square”.

Of course, these are just some possible observations and many more ideas may be highlighted by your students.

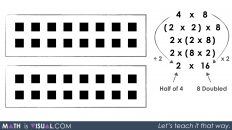
Consider encouraging students to find other equivalent ratios by scaling in tandem (ratio reasoning) or by using the constant of proportionality (rate reasoning) and record their thinking in a ratio table.

Want to Explore These Concepts & Skills Further?

Three (3) additional number talk prompts are available in Day 2 of the Keep It Up problem based math unit that you can dive into now.

Why not start from the beginning of this contextual 8-day unit of real world lessons from the Make Math Moments Problem Based Units page.

Did you use this in your classroom or at home? How’d it go? Post in the comments!

Math IS Visual. Let’s teach it that way.